Skip to main content
SpringerLink
Log in

Unconditionally optimal error estimate of the Crank–Nicolson extrapolation Galerkin finite element method for Kuramoto–Tsuzuki equation

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

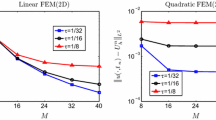
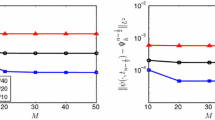
In this paper, a linearized Crank–Nicolson extrapolation Galerkin finite element is investigated for two-dimensional Kuramoto–Tsuzuki equation and the unconditionally optimal error estimate is obtained without any certain time-step restrictions dependent on the spatial mesh size. The key to the analysis is to derive the boundness of the error between finite element approximation and Ritz projection of the exact solution in energy norm in terms of mathematical induction for two cases, i.e., \(\tau \ge h\) and \(\tau \le h\), where \(\tau \) denotes the time-step size and h is the spatial mesh size. Finally, numerical results are provided to confirm the theoretical findings.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

  • Adams R, Fournier J (2003) Sobolev spaces. Academic Press, Amsterdam

    MATH  Google Scholar 

  • Akrivis GD, Dougalis VA, Karakashian OA (1991) On fully discrete Galerkin methods of second-order temporal accuracy for the nonlinear Schrödinger equation. Numer Math 59:31–53

    MathSciNet  MATH  Google Scholar 

  • An R (2016) Optimal error estimates of linearized Crank–Nicolson Galerkin method for Landau–Lifshitz equation. J Sci Comput 69:1–27

    MathSciNet  MATH  Google Scholar 

  • Bao W, Cai Y (2012) Uniform error estimates of finite difference methods for the nonlinear Schrödinger equation with wave operator. SIAM J Numer Anal 50:492–521

    MathSciNet  MATH  Google Scholar 

  • Brenner S, Scott L (2002) The mathematical theory of finite flement methods. Springer, New York

    Google Scholar 

  • Cannon JR, Lin Y (1988) Nonclassical \(H^1\) projection and Galerkin methods for nonlinear parabolic integro-differential equations. SIAM J Numer Anal 25:187–201

    MATH  Google Scholar 

  • Chen ZX (2005) Finite element methods and their applications. Springer, Berlin

    MATH  Google Scholar 

  • Dong XC (2012) A fourth-order split-step pseudospectral scheme for the Kuramoto–Tsuzuki equation. Commun Nonlinear Sci Numer Simul 17(8):3161–3168

    MathSciNet  MATH  Google Scholar 

  • Dupont T, Fairweather G, Johnson JP (1974) Three-level Galerkin methods for parabolic equations. SIAM J Numer Anal 11:392–410

    MathSciNet  MATH  Google Scholar 

  • Gao HD (2014a) Optimal error analysis of Galerkin FEMs for nonlinear Joule heating equations. J Sci Comput 58(3):627–647

    MathSciNet  MATH  Google Scholar 

  • Gao HD (2014b) Optimal error estimates of a linearized backward Euler FEM for the Landau–Lifshitz equation. SIAM J Numer Anal 52:2574–2593

    MathSciNet  MATH  Google Scholar 

  • Gao HD, Qiu WF (2018) Error analysis of mixed finite element methods for nonlinear parabolic equations. J Sci Comput 77(3):1660–1678

    MathSciNet  MATH  Google Scholar 

  • Gao HD, Li BY, Sun WW (2017) Stability and convergence of fully discrete Galerkin FEMs for the nonlinear thermistor equations in a nonconvex polygon. Numer Math 136(2):383–409

    MathSciNet  MATH  Google Scholar 

  • He YN (2008) The Euler implicit/explicit scheme for the 2D time-dependent Navier–Stokes equations with smooth or non-smooth initial data. Math Comput 77:2097–2124

    MathSciNet  MATH  Google Scholar 

  • Heywood JG, Rannacher R (1990) Finite element approximation of the nonstationary Navier–Stokes problem IV: error analysis for second-order time discretization. SIAM J Numer Anal 27:353–384

    MathSciNet  MATH  Google Scholar 

  • Hou YR, Li BY, Sun WW (2013) Error analysis of splitting Galerkin methods for heat and sweat transport in textile materials. SIAM J Numer Anal 51:88–111

    MathSciNet  MATH  Google Scholar 

  • Hu XL, Chen SZ, Chang QS (2015) Fourth-order compact difference schemes for 1D nonlinear Kuramoto–Tsuzuki equation. Numer. Methods Part Differ Equ 31(6):2080–2109

    MathSciNet  MATH  Google Scholar 

  • Kuramoto Y (1984) Chemical oscillations, waves, and turbulence. Springer-Verlag, Berlin, Heidelberg

    MATH  Google Scholar 

  • Kuramoto Y, Tsuzuki T (1975) On the formation of dissipative structures in reaction–diffusion systems. Prog Theor Phys 54:678–699

    Google Scholar 

  • Labidi S, Omrani K (2023) A new approach for numerical solution of Kuramoto–Tsuzuki equation. Appl Numer Math 184:527–541

    MathSciNet  MATH  Google Scholar 

  • Leonaviciene T, Bugajev A, Jankeviciute G, Ciegis R (2016) On stability analysis of finite difference schemes for generalized Kuramoto–Tsuzuki equation with nonlocal boundary conditions. Math Model Anal 21:630–643

    MathSciNet  MATH  Google Scholar 

  • Li Y, Cui XW (2023) Unconditionally optimal error analysis of the second-order BDF finite element method for the Kuramoto–Tsuzuki equaions. J Comput Math 41(2):211–223

    MathSciNet  MATH  Google Scholar 

  • Li BY, Sun WW (2013a) Error analysis of linearized semi-implicit Galerkin finite element methods for nonlinear parabolic equations. Int J Numer Anal Model 10:622–633

    MathSciNet  MATH  Google Scholar 

  • Li BY, Sun WW (2013b) Unconditional convergence and optimal error estimates of a Galerkin-mixed FEM for incompressible miscible flow in porous media. SIAM J Numer Anal 51:1959–1977

    MathSciNet  MATH  Google Scholar 

  • Li DF, Wang JL (2017) Unconditionally optimal error analysis of Crank–Nicolson Galerkin FEMs for a strongly nonlinear parabolic system. J Sci Comput 72:892–915

    MathSciNet  MATH  Google Scholar 

  • Li BY, Gao HD, Sun WW (2014) Unconditionally optimal error estimates of a Crank–Nicolson Galerkin method for the nonlinear thermistor equations. SIAM J Numer Anal 53:933–954

    MathSciNet  MATH  Google Scholar 

  • Li DF, Wang JL, Zhang JW (2017) Unconditionally convergent L1-Galerkin FEMs for nonlinear time fractional Schrödinger equations. SIAM J Sci Comput 39:A3067–A3088

    MATH  Google Scholar 

  • Li DF, Liao HL, Sun WW, Wang JL, Zhang JW (2018a) Analysis of L1-Galerkin FEMs for time fractional nonlinear parabolic problems. Commun Comp Phys 24:86–103

    MathSciNet  MATH  Google Scholar 

  • Li DF, Zhang JW, Zhang ZM (2018b) Unconditionally optimal error estimates of a linearized Galerkin method for nonlinear time fractional reaction-subdiffusion equations. J Sci Comput 76:848–866

    MathSciNet  MATH  Google Scholar 

  • Li DF, Cao WX, Zhang CJ, Zhang ZM (2019) Optimal error estimates of a linearized Crank–Nicolson Galerkin FEM for the Kuramoto–Tsuzuki equations. Commun Comput Phys 26(3):838–854

    MathSciNet  MATH  Google Scholar 

  • Omrani K (2005) Convergence of Galerkin approximations for the Kuramoto–Tsuzuki equation. Numer Methods Partial Differ Equ 21(5):961–975

    MathSciNet  MATH  Google Scholar 

  • Shen J (1990) On an unconditionally stable scheme for the unsteady Navier–Stokes equations. J Comput Math 8:276–288

    MathSciNet  MATH  Google Scholar 

  • Shi DY, Wang JJ (2017) Unconditional superconvergence analysis of a Crank–Nicolson Galerkin FEM for nonlinear Schrödinger equation. J Sci Comput 72:1093–1118

    MathSciNet  MATH  Google Scholar 

  • Shi DY, Yang HJ (2019) Unconditionally optimal error estimates of a new mixed FEM for nonlinear Schrödinger equations. Adv Comput Math 45:3173–3194

    MathSciNet  MATH  Google Scholar 

  • Shi DY, Wang JJ, Yan FN (2017) Unconditional superconvergence analysis for nonlinear parabolic equation with \({{EQ}}_1^{rot}\) nonconforming finite element. J Sci Comput 70(1):85–111

    MathSciNet  MATH  Google Scholar 

  • Sun ZZ (1996) A linearized difference scheme for the Kuramoto–Tsuzuki equation. J Comput Math 14(1):1–7

    MathSciNet  MATH  Google Scholar 

  • Sun WW, Wang JL (2017) Optimal error analysis of Crank-Nicolson schemes for a coupled nonlinear Schrödinger system in 3D. J Comp Appl Math 317:685–699

    MATH  Google Scholar 

  • Sun ZZ, Zhu QD (1998) On Tsertsvadze’s difference scheme for the Kuramoto–Tsuzuki equation. J Comput Appl Math 98(2):289–304

    MathSciNet  MATH  Google Scholar 

  • Thomee V (2006) Galerkin finite element methods for parabolic problems. Springer-Verlag, Berlin, Heidelberg

    MATH  Google Scholar 

  • Tourigny Y (1991) Optimal \(H^1\) estimates for two time-discrete Galerkin approximations of a nonlinear Schrödinger equation. IMA J Numer Anal 11:509–523

    MathSciNet  MATH  Google Scholar 

  • Tsertsvadze GZ (1991) On the convergence of difference schemes for the Kuramoto–Tsuzuki equation and reaction–diffusion type systems. Comput Math Math Phys 31(5):40–47

    MathSciNet  MATH  Google Scholar 

  • Wang JL (2014) A new error analysis of Crank–Nicolson Galerkin FEMs for a generalized nonlinear Schrödinger equation. J Sci Comput 60(2):390–407

    MathSciNet  MATH  Google Scholar 

  • Wang TC, Guo BL (2009) A robust semi-explicit difference scheme for the Kuramoto–Tsuzuki equation. J Comput Appl Math 233:878–888

    MathSciNet  MATH  Google Scholar 

  • Wang SS, Wang TC, Zhang LM, Guo BL (2011) Convergence of a nonlinear finite difference scheme for the Kuramoto–Tsuzuki equation. Commun Nonlinear Sci Numer Simul 16(6):2620–2627

    MathSciNet  MATH  Google Scholar 

  • Zhao X, Sun Z, Hao Z (2014) A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schödinger equation. SIAM J Sci Comput 36:2865–2886

    MathSciNet  Google Scholar 

Download references

Acknowledgements

We would like to thank the anonymous and excellent referees for the constructive comments and valuable suggestions, which greatly improved the original manuscript.

Funding

This work is supported by the National Natural Science Foundation of China (No. 12101568).

Author information

Authors and Affiliations

  1. School of Mathematics, Zhengzhou University of Aeronautics, 450046, Zhengzhou, China

    Huaijun Yang

Authors
  1. Huaijun Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Huaijun Yang.

Ethics declarations

Conflict of interest

We declare that we have no conflicts of interest in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, H. Unconditionally optimal error estimate of the Crank–Nicolson extrapolation Galerkin finite element method for Kuramoto–Tsuzuki equation. Comp. Appl. Math. 42, 259 (2023). https://doi.org/10.1007/s40314-023-02397-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-023-02397-5

Keywords

Mathematics Subject Classification

Search

Navigation