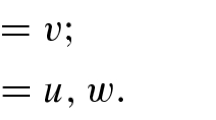Skip to main content
SpringerLink
Log in

Convergence and superconvergence analysis of finite element methods for nonlinear Ginzburg–Landau equation with Caputo derivative

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

In this paper, we study and analyze the time fractional Ginzburg–Landau equation (FGLE) using finite element methods (FEMs) in space and L1 scheme in time. The unconditional optimal \(L^2\)-norm error estimates are obtained based on the time-space error splitting technique. Using the relation between interpolation operator and Ritz projection operator, we obtain the superclose results in \(H^1\)-norm. Furthermore, the global superconvergence results are established through the interpolation postprocessing technique. To overcome the weak singularity of the solution at the initial time and improve the computational efficiency, we adopt the nonuniform L1 scheme in the time direction and built corresponding fast algorithm based on sum-of-exponential technique. Finally, we provide several numerical experiments to verify the theoretical results and demonstrate the advantages of the fast algorithm.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data Statement

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  • Alikhanov AA (2015) A new difference scheme for the time fractional diffusion equation. J Comput Phys 280:424–438

    MathSciNet  MATH  Google Scholar 

  • Aranson IS, Kramer L (2002) The world of the complex Ginzburg–Landau equation. Rev Mod Phys 74(1):99

    MathSciNet  MATH  Google Scholar 

  • Cao J, Xu C (2013) A high order scheme for the numerical solution of the fractional ordinary differential equations. J Comput Phys 238:154–168

    MathSciNet  MATH  Google Scholar 

  • Cao W, Zhang Z, Karniadakis GE (2015) Time-splitting schemes for fractional differential equations I: smooth solutions. SIAM J Sci Comput 37(4):A1752–A1776

    MathSciNet  MATH  Google Scholar 

  • Du Q, Gunzburger MD, Peterson JS (1992) Analysis and approximation of the Ginzburg–Landau model of superconductivity. SIAM Rev 34(1):54–81

    MathSciNet  MATH  Google Scholar 

  • Duan J, Titi E, Holmes P (1993) Regularity, approximation and asymptotic dynamics for a generalized Ginzburg–Landau equation. Nonlinearity 6(6):915–933

    MathSciNet  MATH  Google Scholar 

  • Gao H (2014) Optimal error analysis of Galerkin FEMs for nonlinear Joule heating equations. J Sci Comput 58(3):627–647

    MathSciNet  MATH  Google Scholar 

  • Gao G, Sun Z, Zhang H (2014) A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications. J Comput Phys 259:33–50

    MathSciNet  MATH  Google Scholar 

  • Guan Z, Wang J, Nie Y (2021) Unconditionally optimal error estimates of two linearized Galerkin FEMs for the two-dimensional nonlinear fractional Rayleigh–Stokes problem. Comput Math Appl 93:78–93

    MathSciNet  MATH  Google Scholar 

  • Guan Z, Wang J, Liu Y, Nie Y (2022) Unconditionally optimal convergence of a linearized Galerkin FEM for the nonlinear time-fractional mobile/immobile transport equation. Appl Numer Math 172:133–156

    MathSciNet  MATH  Google Scholar 

  • Hao Z, Sun Z (2016) A linearized high-order difference scheme for the fractional Ginzburg–Landau equation. Numer Methods Partial Differ. Equ. 33(1):105–124

    MathSciNet  MATH  Google Scholar 

  • He D, Pan K (2018) An unconditionally stable linearized difference scheme for the fractional Ginzburg–Landau equation. Numer Algorithms 79:899–925

    MathSciNet  MATH  Google Scholar 

  • Heydari M, Hosseininia M, Atangana A, Avazzadeh Z (2020) A meshless approach for solving nonlinear variable-order time fractional 2D Ginzburg–Landau equation. Eng Anal Bound Elem 120:166–179

    MathSciNet  MATH  Google Scholar 

  • Huo Z, Jia Y (2009) Global well-posedness for the generalized 2D Ginzburg–Landau equation. J Differ Equ 247(1):260–276

    MathSciNet  MATH  Google Scholar 

  • Jiang S, Zhang J, Zhang Q, Zhang Z (2017) Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations. Commun Comput Phys 21(3):650–678

    MathSciNet  MATH  Google Scholar 

  • Langlands T, Henry BI (2005) The accuracy and stability of an implicit solution method for the fractional diffusion equation. J Comput Phys 205(2):719–736

    MathSciNet  MATH  Google Scholar 

  • Li M (2022) Cut-off error splitting technique for conservative nonconforming VEM for N-coupled nonlinear Schrödinger–Boussinesq equations. J Sci Comput 93(3):1–44

    MathSciNet  MATH  Google Scholar 

  • Li B, Sun W (2012) Error analysis of linearized semi-implicit Galerkin finite element methods for nonlinear parabolic equations. Int J Numer Anal Model 10(3):622–633

  • Li B, Sun W (2013) Unconditional convergence and optimal error estimates of a Galerkin-mixed FEM for incompressible miscible flow in porous media. SIAM J Numer Anal 51(4):1959–1977

    MathSciNet  MATH  Google Scholar 

  • Li D, Wang J (2017) Unconditionally optimal error analysis of Crank–Nicolson Galerkin FEMs for a strongly nonlinear parabolic system. J Sci Comput 72(2):892–915

    MathSciNet  MATH  Google Scholar 

  • Li M, Zhao Y (2018) A fast energy conserving finite element method for the nonlinear fractional Schrödinger equation with wave operator. Appl Math Comput 338:758–773

    MathSciNet  MATH  Google Scholar 

  • Li D, Liao H, Sun W, Wang J, Zhang J (2018) Analysis of L1-Galerkin FEMs for time-fractional nonlinear parabolic problems. Commun Comput Phys, 24(1):86–103

  • Li M, Huang C, Wang N (2017a) Galerkin finite element method for the nonlinear fractional Ginzburg–Landau equation. Appl Numer Math 118:131–149

  • Li D, Wang J, Zhang J (2017b) Unconditionally convergent L1-Galerkin FEMs for nonlinear time-fractional Schrödinger equations. SIAM J Sci Comput 39(6):A3067–A3088

  • Li D, Zhang J, Zhang Z (2018) Unconditionally optimal error estimates of a linearized Galerkin method for nonlinear time fractional reaction–subdiffusion equations. J Sci Comput 76(2):848–866

    MathSciNet  MATH  Google Scholar 

  • Li M, Shi D, Wang J (2020) Unconditional superconvergence analysis of a linearized Crank–Nicolson Galerkin FEM for generalized Ginzburg–Landau equation. Comput Math Appl 79(8):2411–2425

    MathSciNet  MATH  Google Scholar 

  • Liao H, Li D, Zhang J (2018a) Sharp error estimate of the nonuniform L1 formula for linear reaction–subdiffusion equations. SIAM J Numer Anal 56(2):1112–1133

  • Liao H, McLean W, Zhang J (2019a) A discrete Grönwall inequality with applications to numerical schemes for subdiffusion problems. SIAM J Numer Anal 57(1):218–237

  • Liao H, Yan Y, Zhang J (2019b) Unconditional convergence of a two-level linearized fast algorithm for nonlinear subdiffusion equations. J Sci Comput 80(1):1–25

  • Lin Y, Xu C (2007) Finite difference/spectral approximations for the time-fractional diffusion equation. J Comput Phys 225(2):1533–1552

    MathSciNet  MATH  Google Scholar 

  • Milovanov AV, Rasmussen JJ (2005) Fractional generalization of the Ginzburg–Landau equation: an unconventional approach to critical phenomena in complex media. Phys Lett A 337(1):75–80

    MATH  Google Scholar 

  • Mustapha K (2015) Time-stepping discontinuous Galerkin methods for fractional diffusion problems. Numer Math 130(3):497–516

    MathSciNet  MATH  Google Scholar 

  • Mustapha K, AlMutawa J (2012) A finite difference method for an anomalous sub-diffusion equation, theory and applications. Numer Algorithms 61(4):525–543

    MathSciNet  MATH  Google Scholar 

  • Mvogo A, Tambue A, Ben-Bolie GH, Kofané TC (2016) Localized numerical impulse solutions in diffuse neural networks modeled by the complex fractional Ginzburg–Landau equation. Commun Nonlinear Sci Numer Simul 39:396–410

    MathSciNet  MATH  Google Scholar 

  • Pu X, Guo B (2011) Well-posedness and dynamics for the fractional Ginzburg–Landau equation. Appl Anal 92(2):318–334

    MathSciNet  MATH  Google Scholar 

  • Raza N (2018) Exact periodic and explicit solutions of the conformable time fractional Ginzburg-Landau equation. Opt Quantum Electron 50(3):154

  • Shi D, Wang J (2017) Unconditional superconvergence analysis of a Crank–Nicolson Galerkin FEM for nonlinear Schrödinger equation. J Sci Comput 72(3):1093–1118

    MathSciNet  MATH  Google Scholar 

  • Shi D, Wang F, Fan M, Zhao Y (2015) A new approach of the lowest order anisotropic mixed finite element high accuracy analysis for nonlinear sine-Gordon equations. Math Numer Sin 37(2):148

    MathSciNet  MATH  Google Scholar 

  • Shi D, Yan F, Wang J (2016) Unconditional superconvergence analysis of a new mixed finite element method for nonlinear Sobolev equation. Appl Math Comput 274:182–194

    MathSciNet  MATH  Google Scholar 

  • Skarka V, Aleksić N (2006) Stability criterion for dissipative soliton solutions of the one-, two-, and three-dimensional complex cubic–quintic Ginzburg–Landau equations. Phys Rev Lett 96(1):013903

    Google Scholar 

  • Sun Z, Wu X (2006) A fully discrete difference scheme for a diffusion-wave system. Appl Numer Math 56(2):193–209

    MathSciNet  MATH  Google Scholar 

  • Tarasov VE (2006) Psi-series solution of fractional Ginzburg–Landau equation. Math Gen 39(26):8395–8407

    MathSciNet  MATH  Google Scholar 

  • Tarasov VE, Zaslavsky GM (2005) Fractional Ginzburg–Landau equation for fractal media. Phys A: Stat Mech Appl 354:249–261

    Google Scholar 

  • Thomée V (2007) Galerkin finite element methods for parabolic problems. Springer Science & Business Media, Berlin

    MATH  Google Scholar 

  • Wang J (2014) A new error analysis of Crank–Nicolson Galerkin FEMs for a generalized nonlinear Schrödinger equation. J Sci Comput 60(2):390–407

    MathSciNet  MATH  Google Scholar 

  • Wang P (2021) Fast exponential time differencing/spectral-Galerkin method for the nonlinear fractional Ginzburg–Landau equation with fractional Laplacian in unbounded domain. Appl Math Lett 112:106710

    MathSciNet  MATH  Google Scholar 

  • Wang F, Zhao Y, Chen C, Wei Y, Tang Y (2019) A novel high-order approximate scheme for two-dimensional time-fractional diffusion equations with variable coefficient. Comput Math Appl 78(5):1288–1301

    MathSciNet  MATH  Google Scholar 

  • Weitzner H, Zaslavsky GM (2003) Some applications of fractional equations. Commun Nonlinear Sci Numer Simul 8(3):273–281

    MathSciNet  MATH  Google Scholar 

  • Yan Y, Sun Z, Zhang J (2017) Fast evaluation of the Caputo fractional derivative and its applications to fractional diffusion equations: a second order scheme. Commun Comput Phys 22(4):1028–1048

    MathSciNet  MATH  Google Scholar 

  • Zhang M, Zhang G (2021) Fast iterative solvers for the two-dimensional spatial fractional Ginzburg–Landau equations. Appl Math Lett 121:107350

    MathSciNet  MATH  Google Scholar 

  • Zhang Y, Sun Z, Liao H (2014) Finite difference methods for the time fractional diffusion equation on non-uniform meshes. J Comput Phys 265:195–210

    MathSciNet  MATH  Google Scholar 

  • Zhang Q, Li Y, Su M (2019a) The local and global existence of solutions for a time fractional complex Ginzburg–Landau equation. J Math Anal Appl 469(1):16–43

    MathSciNet  MATH  Google Scholar 

  • Zhang Z, Li M, Wang Z (2019b) A linearized Crank–Nicolson Galerkin FEMs for the nonlinear fractional Ginzburg–Landau equation. Appl Anal 98(15):2648–2667

    MathSciNet  MATH  Google Scholar 

  • Zhang L, Zhang Q, Sun H (2020) Exponential Runge–Kutta method for two-dimensional nonlinear fractional complex Ginzburg–Landau equations. J Sci Comput 83:59

    MathSciNet  MATH  Google Scholar 

  • Zhang Q, Zhang L, Sun H (2021) A three-level finite difference method with preconditioning technique for two-dimensional nonlinear fractional complex Ginzburg–Landau equations. J Comput Appl Math 389:113355

    MathSciNet  MATH  Google Scholar 

  • Zhao X, Sun Z, Hao Z (2014) A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schrödinger equation. SIAM J Sci Comput 36(6):A2865–A2886

    MATH  Google Scholar 

  • Zhuang P, Liu F, Anh V, Turner I (2009) Stability and convergence of an implicit numerical method for the non-linear fractional reaction–subdiffusion process. IMA J Appl Math 74(5):645–667

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The work is supported by the China Postdoctoral Science Foundation (2023T160589), National Natural Science Foundation of China (nos. 11801527, 11971416), Natural Science Foundation of Henan Province (222300420256), Training Plan of Young Backbone Teachers in Colleges of Henan Province (no. 2020GGJS230), Henan University Science and Technology Innovation Talent support program (19HASTIT025).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Zhengzhou University, Zhengzhou, 450001, China

    Fang Chen & Meng Li

  2. Henan Joint International Research Laboratory of High Performance Computation for Complex Systems, School of Science, Xuchang University, Xuchang, 461000, China

    Fang Chen & Yanmin Zhao

  3. LSEC, ICMSEC, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, China

    Yifa Tang

  4. School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing, 100049, China

    Yifa Tang

Authors
  1. Fang Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Meng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yanmin Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yifa Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Meng Li or Yanmin Zhao.

Ethics declarations

Conflict of interest

The authors declare that we have no conflict of interest.

Additional information

Communicated by Agnieszka Malinowska.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, F., Li, M., Zhao, Y. et al. Convergence and superconvergence analysis of finite element methods for nonlinear Ginzburg–Landau equation with Caputo derivative. Comp. Appl. Math. 42, 271 (2023). https://doi.org/10.1007/s40314-023-02409-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-023-02409-4

Keywords

Mathematics Subject Classification

Search

Navigation