Limiting behaviour of non-autonomous Caputo-type time-delay systems and initial-time on the real number line

Abstract

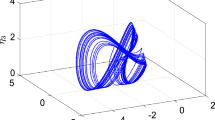
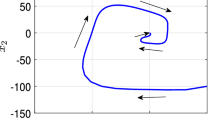
In many emerging scientific applications, the input of random initial time is often required for predicting and controlling the dynamics of real-order systems that include or does not include time-delays. In this work, we provide a new design for a class of random initial-time non-autonomous linear Caputo-type real-order time-delay systems that involves constant discrete delays. We first introduce a new comparison principle and a linear comparison lemma for Caputo derivative. By using the idea of comparison methodology and generalized Laplace transform, we develop some new elementary asymptotic theories and establish order-dependent and delay-independent conditions that give convergence of nontrivial solutions to such a class of system. One of the major challenges encountered in the investigation is discovering some simpler classes of autonomous linear real-order systems in bounding the coefficient matrices of a designed class of systems above by constant matrices in our assumptions. These assumptions including newly introduced matrices $\Lambda$, $\Theta _{k}$ and G provide some fundamental key tools for an effective asymptotic analysis of newly designed class of systems. A typical theorem that we develop says that if all the diagonal entries of $\Lambda$ become negative and every root of the characteristic equation associated with the matrix $\Lambda +\sum \nolimits _{k=1}^{m}\Theta _{k}G$ lies in the open left-half complex plane, then it is possible to predict the limiting behavior of the designed class of systems. For a practical application of interest, we show how to synchronize the possible chaotic dynamics of the coupled nonlinear Duffing oscillators if the system starts at a negative initial time through some proposed results.