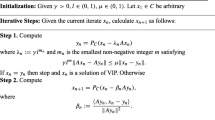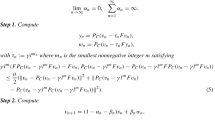Skip to main content
SpringerLink
Log in

Linearized Douglas–Rachford method for variational inequalities with Lipschitz mappings

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

In this article, we introduce linearized Douglas–Rachford method for solving Lipschitz continuous variational inequalities in Hilbert space. First, we show the linear convergence of linearized Douglas–Rachford method with the fixed stepsize for the strongly monotone mapping. The usual drawback of algorithms with the fixed stepsize is the requirement to know the Lipschitz constant of the mapping. To avoid this, we present linearized Douglas–Rachford method with the diminishing stepsize whose convergence is established for the strongly pseudomonotone mapping. Finally, preliminary results from numerical experiments are promising.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Fig. 1
Fig. 2

Similar content being viewed by others

Data availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  • Antipin AS (1976) On a method for convex programs using a symmetrical modification of the Lagrange function. Ekon Mat Metody 12:1164–1173

    Google Scholar 

  • Bauschke HH, Combettes PL (2017) Convex analysis and monotone operator theory in Hilbert spaces, 2nd edn. Springer, Berlin

    Book  MATH  Google Scholar 

  • Bello Cruz JY, Iusem AN (2010) Convergence of direct methods for paramonotone variational inequalities. Comput Optim Appl 46:247–263

    Article  MathSciNet  MATH  Google Scholar 

  • Berinde V (2006) Iterative approximation of fixed points. Springer, Berlin

    MATH  Google Scholar 

  • Bertsekas DP (1999) Nonlinear programming. Athena Scientific, Cambridge

    MATH  Google Scholar 

  • Byrne C (2004) A unified treatment of some iterative algorithms in signal processing and image reconstruction. Inverse Probl 20:103–120

    Article  MathSciNet  MATH  Google Scholar 

  • Censor Y, Gibali A, Reich S (2011) The subgradient extragradient method for solving variational inequalities in Hilbert space. J Optim Theory Appl 148:318–335

    Article  MathSciNet  MATH  Google Scholar 

  • Dong QL, Cho YJ, Zhong LL, Rassias ThM (2018) Inertial projection and contraction algorithms for variational inequalities. J Glob Optim 70:687–704

    Article  MathSciNet  MATH  Google Scholar 

  • Dong QL, Gibali A, Jiang D, Ke SH (2018) Convergence of projection and contraction algorithms with outer perturbations and their applications to sparse signals recovery. J Fixed Point Theory Appl 20:16

    Article  MathSciNet  MATH  Google Scholar 

  • Dong QL, He S, Rassias MT (2021) General splitting methods with linearization for the split feasibility problem. J Glob Optim 79:813–836

    Article  MathSciNet  MATH  Google Scholar 

  • Dong QL, He S, Liu L (2021) A general inertial projected gradient method for variational inequality problems. Comput Appl Math 40:168

    Article  MathSciNet  MATH  Google Scholar 

  • Facchinei F, Pang JS (2003) Finite-dimensional variational inequalities and complementarity problems. Springer series in operations research, vol I and II. Springer, New York

    MATH  Google Scholar 

  • Hai TN (2020) On gradient projection methods for strongly pseudomonotone variational inequalities without Lipschitz continuity. Optim Lett 14:1177–1191

    Article  MathSciNet  MATH  Google Scholar 

  • Harker PT, Pang JS (1990) A damped-Newton method for the linear complementarity problem. In: Allgower G, Georg K (eds) Computational solution of nonlinear systems of equations, lectures in appl. Math., vol. 26. AMS, Providence, pp 265–284

  • He B (1997) A class of projection and contraction methods for monotone variational inequalities. Appl Math Optim 35:69–76

    Article  MathSciNet  MATH  Google Scholar 

  • Hieu DV, Thong DV (2018) New extragradient-like algorithms for strongly pseudo-monotone variational inequalities. J Glob Optim 70:385–399

    Article  MATH  Google Scholar 

  • Khanh PD, Vuong PT (2014) Modified projection method for strongly pseudomonotone variational inequalities. J Glob Optim 58:341–350

    Article  MathSciNet  MATH  Google Scholar 

  • Korpelevich GM (1976) The extragradient method for finding saddle points and other problems. Ekon Mat Metody 12:747–756

    MathSciNet  MATH  Google Scholar 

  • Mainge PE, Gobinddass ML (2016) Convergence of one-step projected gradient methods for variational inequalities. J Optim Theory Appl 171:146–168

    Article  MathSciNet  MATH  Google Scholar 

  • Malitsky Y (2015) Projected reflected gradient methods for variational inequalities. SIAM J Optim 25(1):502–520

    Article  MathSciNet  MATH  Google Scholar 

  • Malitsky YV, Semenov VV (2014) An extragradient algorithm for monotone variational inequalities. Cybern Syst Anal 50:271–277

    Article  MathSciNet  MATH  Google Scholar 

  • Shehu Y, Iyiola OS (2020) Projection methods with alternating inertial steps for variational inequalities: weak and linear convergence. Appl Numer Math 157:315–337

    Article  MathSciNet  MATH  Google Scholar 

  • Solodov MV, Svaiter BF (1999) A new projection method for variational inequality problems. SIAM J Control Optim 37:765–776

    Article  MathSciNet  MATH  Google Scholar 

  • Thong DV, Hieu DV (2018) Inertial extragradient algorithms for strongly pseudomonotone variational inequalities. J Comput Appl Math 341:80–98

    Article  MathSciNet  MATH  Google Scholar 

  • Tseng P (2000) A modified forward-backward splitting method for maximal monotone mappings. SIAM J Control Optim 38:431–446

    Article  MathSciNet  MATH  Google Scholar 

  • Yang Q (2005) On variable-step relaxed projection algorithm for variational inequalities. J Math Anal Appl 302:166–79

    Article  MathSciNet  MATH  Google Scholar 

  • Yang J, Liu H (2018) A modified projected gradient method for monotone variational inequalities. J Optim Theory Appl 179:197–211

    Article  MathSciNet  MATH  Google Scholar 

  • Yao Y, Marino G, Muglia L (2014) A modified Korpelevich’s method convergent to the minimum-norm solution of a variational inequality. Optimization 63:559–569

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like to express their deep gratitude to the anonymous referee for the valuable comments and suggestions, which led to a large improvement of the manuscript. The authors are grateful to Professor Songnian He for helpful discussion in Lemma 5, Example 1 and Remark 3. This work was Scientific Research Project of Aeronautical Science Foundation of China (20200008067001).

Author information

Authors and Affiliations

  1. College of Science, Civil Aviation University of China, Tianjin, 300300, China

    Qiao-Li Dong

Authors
  1. Qiao-Li Dong
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Qiao-Li Dong.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Communicated by Andreas Fischer.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dong, QL. Linearized Douglas–Rachford method for variational inequalities with Lipschitz mappings. Comp. Appl. Math. 42, 319 (2023). https://doi.org/10.1007/s40314-023-02466-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-023-02466-9

Keywords

Mathematics Subject Classification

Search

Navigation