Skip to main content
SpringerLink
Log in

An approach for solving fully generalized intuitionistic fuzzy transportation problems

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

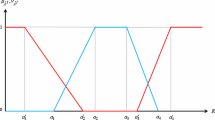
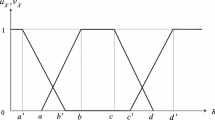
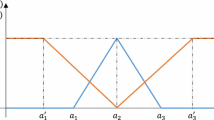
Abstract

In this paper, we study the transportation problem defined as generalized triangular intuitionistic fuzzy transportation problem (GTIFTP). To handle the above-defined transportation problem, we propose a new criteria for ordering generalized triangular intuitionistic fuzzy numbers (GTIFNs). We define this ordering on index of optimism-based expected value of GTIFN, which can also be used to deal with various other optimization problems. We discuss limitations of some of the existing ranking approaches for intuitionistic fuzzy numbers. Further, we discuss the reasonable properties of this ordering method. We also suggest a new algorithm to solve GTIFTPs, which is numerically efficient and involves less complex calculations than the existing methods. To illustrate our proposed approach and to make it more understandable, we solve three numerical examples with parameters in different combinations of GTIFNs, triangular intuitionistic fuzzy numbers and crisp numbers. Comparative analysis of this method is also done with some existing methods and we finally draw some conclusions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Data availability

The datasets generated and/or analyzed during the current study are included in this article. And if more information is needed, it is available from the corresponding author on reasonable request.

References

  • Aggarwal S, Gupta C (2014) A novel algorithm for solving intuitionistic fuzzy transportation problem via new ranking method. Ann Fuzzy Math Inform 8(5):753–768

    MathSciNet  MATH  Google Scholar 

  • Antony RJP, Savarimuthu SJ, Pathinathan T (2014) Method for solving the transportation problem using triangular intuitionistic fuzzy number. Int J Comput Algorithm 3(1):590–605

    Google Scholar 

  • Arun Prakash K, Suresh M, Vengataasalam S (2016) A new approach for ranking of intuitionistic fuzzy numbers using a centroid concept. Math Sci 10(4):177–184

    MathSciNet  MATH  Google Scholar 

  • Atanassov KT, Atanassov KT (1999) Intuitionistic fuzzy sets. Physica-Verlag, Heidelberg, pp 1–137

    MATH  Google Scholar 

  • Beg I, Rashid T (2014) Multi-criteria trapezoidal valued intuitionistic fuzzy decision making with Choquet integral based TOPSIS. Opsearch 51(1):98–129

    MathSciNet  MATH  Google Scholar 

  • Beg I, Rashid T (2016) An intuitionistic 2-tuple linguistic information model and aggregation operators. Int J Intell Syst 31(6):569–592

    Google Scholar 

  • Bharati SK (2021) Transportation problem with interval-valued intuitionistic fuzzy sets: impact of a new ranking. Prog Artif Intell 10(2):129–145

    MathSciNet  Google Scholar 

  • Bhaumik A, Roy SK, Li DF (2021) \((\alpha,\beta,\gamma ) \)-cut set based ranking approach to solving bi-matrix games in neutrosophic environment. Soft Comput 25(4):2729–2739

    Google Scholar 

  • Bisht M, Dangwal R (2022) Solving interval-valued transportation problem using a new ranking function for octagonal fuzzy numbers. Int J Model Simul Sci Comput 13(5):2250039

    Google Scholar 

  • Bisht M, Dangwal R (2023) Fuzzy ranking approach to bi-matrix games with interval payoffs in marketing-management problem. Int Game Theory Rev 25(01):2250016

    MathSciNet  MATH  Google Scholar 

  • Chakraborty D, Jana DK, Roy TK (2015) Arithmetic operations on generalized intuitionistic fuzzy number and its applications to transportation problem. Opsearch 52:431–471

    MathSciNet  MATH  Google Scholar 

  • Chhibber D, Bisht DC, Srivastava PK (2021) Pareto-optimal solution for fixed-charge solid transportation problem under intuitionistic fuzzy environment. Appl Soft Comput 107:107368

    Google Scholar 

  • Chutia R, Smarandache F (2022) Ranking of single-valued neutrosophic numbers through the index of optimism and its reasonable properties. Artif Intell Rev 55(2):1489–1518

    Google Scholar 

  • De PK, Das D (2014) A study on ranking of trapezoidal intuitionistic fuzzy numbers. Int J Comput Inf Syst Ind Manag Appl 6:437–444

    Google Scholar 

  • De SK, Sana SS (2018) The (p, q, r, l) model for stochastic demand under intuitionistic fuzzy aggregation with Bonferroni mean. J Intell Manuf 29(8):1753–1771

    Google Scholar 

  • Dhankhar C, Kumar K (2023) Multi-attribute decision-making based on the advanced possibility degree measure of intuitionistic fuzzy numbers. Granul Comput 8(3):467–478

    Google Scholar 

  • Di Caprio D, Ebrahimnejad A, Alrezaamiri H, Santos-Arteaga FJ (2022) A novel ant colony algorithm for solving shortest path problems with fuzzy arc weights. Alex Eng J 61(5):3403–3415

    Google Scholar 

  • Dubey D, Mehra A (2011) Linear programming with triangular intuitionistic fuzzy number. In: Proceedings of the 7th conference of the European Society for Fuzzy Logic and Technology. Atlantis Press, pp 563–569

  • Ebrahimnejad A (2016) Fuzzy linear programming approach for solving transportation problems with interval-valued trapezoidal fuzzy numbers. Sādhanā 41(3):299–316

    MathSciNet  MATH  Google Scholar 

  • Ebrahimnejad A, Verdegay JL (2016) An efficient computational approach for solving type-2 intuitionistic fuzzy numbers based transportation problems. Int J Comput Intell Syst 9(6):1154–1173

    Google Scholar 

  • Ebrahimnejad A, Verdegay JL (2018) A new approach for solving fully intuitionistic fuzzy transportation problems. Fuzzy Optim Decis Mak 17(4):447–474

    MathSciNet  MATH  Google Scholar 

  • Ebrahimnejad A, Tavana M, Charles V (2022) Analytics under uncertainty: a novel method for solving linear programming problems with trapezoidal fuzzy variables. Soft Comput 26:327–347

    Google Scholar 

  • Gani AN, Abbas S (2012) Solving intuitionistic fuzzy transportation problem using zero suffix algorithm. Int J Math Sci Eng Appl 6:73–82

    MathSciNet  Google Scholar 

  • Gani AN, Abbas S (2013) A new method for solving intuitionistic fuzzy transportation problem. Appl Math Sci 7(28):1357–1365

    Google Scholar 

  • Garg H, Rani D (2022) Novel distance measures for intuitionistic fuzzy sets based on various triangle centers of isosceles triangular fuzzy numbers and their applications. Expert Syst Appl 191:116228

    Google Scholar 

  • Garg H, Sugapriya C, Kuppulakshmi V, Nagarajan D (2023) Optimization of fuzzy inventory lot-size with scrap and defective items under inspection policy. Soft Comput 27(5):2231–2250

    Google Scholar 

  • Gazi KH, Mondal SP, Chatterjee B, Ghorui N, Ghosh A, De D (2023) A new synergistic strategy for ranking restaurant locations: a decision-making approach based on the hexagonal fuzzy numbers. RAIRO-Oper Res 57(2):571–608

    MATH  Google Scholar 

  • Ghosh S, Roy SK, Ebrahimnejad A, Verdegay JL (2021) Multi-objective fully intuitionistic fuzzy fixed-charge solid transportation problem. Complex Intell Syst 7:1009–1023

    Google Scholar 

  • Hitchcock FL (1941) The distribution of a product from several sources to numerous localities. J Math Phys 20(1–4):224–230

    MathSciNet  MATH  Google Scholar 

  • Hussain RJ, Kumar PS (2012) Algorithmic approach for solving intuitionistic fuzzy transportation problem. Appl Math Sci 6(80):3981–3989

    MathSciNet  MATH  Google Scholar 

  • Jansi Rani J, Dhanasekar S, Manivannan A, Micheal DR (2023) On solving fully intuitionistic fuzzy transportation problem via branch and bound technique. J Intell Fuzzy Syst 44(4):6219–6229

    Google Scholar 

  • Jeevaraj S, Rajesh R, Lakshmana Gomathi Nayagam V (2023) A complete ranking of trapezoidal-valued intuitionistic fuzzy number: an application in evaluating social sustainability. Neural Comput Appl 35(8):5939–5962

    Google Scholar 

  • Kamini Sharma MK (2020) Zero-point maximum allocation method for solving intuitionistic fuzzy transportation problem. Int J Appl Comput Math 6(4):1–11

    MathSciNet  MATH  Google Scholar 

  • Kaufman A, Gupta MM (1991) Introduction to fuzzy arithmetic. Van Nostrand Reinhold Company, New York

    Google Scholar 

  • Kumar A, Kaur M (2013) A ranking approach for intuitionistic fuzzy numbers and its application. J Appl Res Technol 11(3):381–396

    Google Scholar 

  • Kumar PS, Hussain RJ (2016) Computationally simple approach for solving fully intuitionistic fuzzy real life transportation problems. Int J Syst Assur Eng Manag 7:90–101

    Google Scholar 

  • Li DF (2010) A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems. Comput Math Appl 60(6):1557–1570

    MathSciNet  MATH  Google Scholar 

  • Mahmoodirad A, Allahviranloo T, Niroomand S (2019) A new effective solution method for fully intuitionistic fuzzy transportation problem. Soft Comput 23(12):4521–4530

    MATH  Google Scholar 

  • Midya S, Roy SK, Yu VF (2021) Intuitionistic fuzzy multi-stage multi-objective fixed-charge solid transportation problem in a green supply chain. Int J Mach Learn Cybern 12(3):699–717

    Google Scholar 

  • Mitchell HB (2004) Ranking-intuitionistic fuzzy numbers. Int J Uncertain Fuzziness Knowl Based Syst 12(03):377–386

    MathSciNet  MATH  Google Scholar 

  • Mondal A, Roy SK, Midya S (2023) Intuitionistic fuzzy sustainable multi-objective multi-item multi-choice step fixed-charge solid transportation problem. J Ambient Intell Humaniz Comput 14(6):6975–6999

    Google Scholar 

  • Nasir VK, Beenu VP (2022) Transportation problem with heptagonal intuitionistic fuzzy number solved using value index and ambiguity index. Math Stat Eng Appl 71(4):3345–3353

    Google Scholar 

  • Nayagam VLG, Venkateshwari G, Sivaraman G (2008) Ranking of intuitionistic fuzzy numbers. In: 2008 IEEE international conference on fuzzy systems (IEEE World Congress on Computational Intelligence). IEEE, pp 1971–1974

  • Nehi HM (2010) A new ranking method for intuitionistic fuzzy numbers. Int J Fuzzy Syst 12:1

    MathSciNet  Google Scholar 

  • Pramila K, Uthra G (2014) Optimal solution of an intuitionistic fuzzy transportation problem. Ann Pure Appl Math 8(2):67–73

    Google Scholar 

  • Ramesh J (1976) Decision making in the presence of fuzzy variables

  • Rani D, Ebrahimnejad A, Gupta G (2022) Generalized techniques for solving intuitionistic fuzzy multi-objective non-linear optimization problems. Expert Syst Appl 202:117264

    Google Scholar 

  • Sanjana R, Ramesh G (2022) A novel approach to interval-valued variables using new interval arithmetic to solve an intuitionistic fuzzy transportation problem. J Intell Fuzzy Syst 43(5):6783–6792

    Google Scholar 

  • Seikh MR, Nayak PK, Pal M (2012) Generalized triangular fuzzy numbers in intuitionistic fuzzy environment. Int J Eng Res Dev 5:08–13

    Google Scholar 

  • Shivani Rani D, Ebrahimnejad A (2022) An approach to solve an unbalanced fully rough multi-objective fixed-charge transportation problem. Comput Appl Math 41(4):129

    MathSciNet  MATH  Google Scholar 

  • Singh SK, Yadav SP (2015) Efficient approach for solving type-1 intuitionistic fuzzy transportation problem. Int J Syst Assur Eng Manag 6(3):259–267

    Google Scholar 

  • Singh SK, Yadav SP (2016a) A new approach for solving intuitionistic fuzzy transportation problem of type-2. Ann Oper Res 243(1):349–363

  • Singh SK, Yadav SP (2016b) A novel approach for solving fully intuitionistic fuzzy transportation problem. Int J Oper Res 26(4):460–472

  • Wang X, Kerre EE (2001a) Reasonable properties for the ordering of fuzzy quantities (I). Fuzzy Sets Syst 118(3):375–385

  • Wang X, Kerre EE (2001b) Reasonable properties for the ordering of fuzzy quantities (II). Fuzzy Sets Syst 118(3):387–405

  • Wang JQ, Nie R, Zhang HY, Chen XH (2013) New operators on triangular intuitionistic fuzzy numbers and their applications in system fault analysis. Inf Sci 251:79–95

    MathSciNet  MATH  Google Scholar 

  • Yogashanthi T, Sathish S, Ganesan K (2023) Generalized intuitionistic fuzzy flow shop scheduling problem with setup time and single transport facility. Int J Fuzzy Logic Intell Syst 23(1):34–43

    Google Scholar 

Download references

Acknowledgements

Monika Bisht and Shivam Rawat would like to thank the CSIR-HRDG Fund, under grant EMR-09/386(0065)/2020-EMR-1 and EMR-09/386(0064)/2019-EMR-1, respectively, for financial support.

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistical Sciences, Lahore School of Economics, Lahore, 53200, Pakistan

    Ismat Beg

  2. Department of Mathematics, H.N.B. Garhwal University, BGR Campus, Pauri Garhwal, Uttarakhand, 246001, India

    Monika Bisht

  3. Department of Mathematics, Graphic Era Hill University, Dehradun Campus, Dehradun, Uttarakhand, 248001, India

    Monika Bisht

  4. Department of Mathematics, Graphic Era Deemed to be University, Dehradun, Uttarakhand, 248002, India

    Shivam Rawat

Authors
  1. Ismat Beg
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Monika Bisht
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shivam Rawat
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Monika Bisht.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Beg, I., Bisht, M. & Rawat, S. An approach for solving fully generalized intuitionistic fuzzy transportation problems. Comp. Appl. Math. 42, 329 (2023). https://doi.org/10.1007/s40314-023-02467-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-023-02467-8

Keywords

Mathematics Subject Classification

Search

Navigation