Abstract
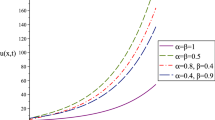
In this paper, we present how to apply the invariant subspace method for finding the linear invariant product spaces and exact solutions of the coupled system of time-fractional nonlinear partial differential equations (NPDEs). We study how the invariant subspace method helps to reduce the coupled system of time-fractional NPDEs into the system of time-fractional ODEs. More specifically, we demonstrate the applicability and efficiency of this method by constructing different finite-dimensional linear invariant product spaces for the nonlinear coupled system of time-fractional convection–reaction–diffusion equations. Additionally, we explain how to find the exact solutions of the quadratic and cubic nonlinear coupled system of time-fractional convection–reaction–diffusion equations along with appropriate initial and boundary conditions. Also, we present 2D and 3D plots for some obtained analytical solutions with different values of fractional orders \(\alpha _i,i=1,2.\) In addition, we observe that the obtained analytic solutions can be expressed in terms of Mittag–Leffler, polynomial, exponential, and trigonometric functions.




Similar content being viewed by others
Data availability
Not applicable.
References
Axler S (2014) Linear algebra done right. Springer, Heidelberg
Bagley RL, Torvik PJ (1984) On the appearance of the fractional derivative in the behavior of real materials. ASME J Appl Mech 51:294–298
Bakkyaraj T, Sahadevan R (2015) Group formalism of Lie transformations to time-fractional partial differential equations. Pramana-J Phys 85:849–860
Cherniha R, Davydovych V (2017) Nonlinear reaction-diffusion systems: conditional symmetry. Exact solutions and their applications in biology. Springer, Bern
Choudhary S, Daftardar-Gejji V (2017) Invariant subspace method: a tool for solving fractional partial differential equations. Fract Calc Appl Anal 20:477–493
Choudhary S, Daftardar-Gejji V (2019) Solving systems of multi-term fractional PDEs: invariant subspace approach. Int J Model Simul Sci Comput 10(1):1941010
Choudhary S, Prakash P, Daftardar-Gejji V (2019) Invariant subspaces and exact solutions for a system of fractional PDEs in higher dimensions. Comput Appl Math 38:126
Chu YM, Inc M, Hashemi MS, Eshaghi S (2022) Analytical treatment of regularized Prabhakar fractional differential equations by invariant subspaces. Comput Appl Math 41:271
Daftardar-Gejji V, Jafari H (2005) Adomian decomposition: a tool for solving a system of fractional differential equations. J Math Anal Appl 301:508–518
Datsko B, Gafiychuk V (2018) Complex spatio-temporal solutions in fractional reaction-diffusion systems near a bifurcation point. Fract Calc Appl Anal 21:237–253
Datsko B, Luchko Y, Gafiychuk V (2012) Pattern formation in fractional reaction-diffusion systems with multiple homogeneous states. Int J Bifurc Chaos 22:1250087
Diethelm K (2010) The analysis of fractional differential equations. Springer, Berlin
Galaktionov VA, Svirshchevskii SR (2007) Exact solutions and invariant subspaces of nonlinear partial differential equations in mechanics and physics. Chapman and Hall/CRC, London
Garra R, Tomovski Z (2021) Exact results on some nonlinear Laguree-type diffusion equations. Math Model Anal 26:72–81
Gazizov RK, Kasatkin AA (2013) Construction of exact solutions for fractional order differential equations by invariant subspace method. Comput Math Appl 66:576–584
Harris PA, Garra R (2013) Analytic solution of nonlinear fractional Burgers-type equation by invariant subspace method. Nonlinear Stud 20:471–481
Harris PA, Garra R (2017) Nonlinear heat conduction equations with memory: physical meaning and analytical results. J. Math. Phys. 58:063501
Ionescu C, Lopes A, Copot D, Machado JAT, Bates JHT (2017) The role of fractional calculus in modeling biological phenomena: a review. Commun Nonlinear Sci Numer Simul 51:141–159
Jafari H, Momani S (2007) Solving fractional diffusion and wave equations by modified homotopy perturbation method. Phys Lett A 370:388–396
Jafari H, Seifi S (2009) Homotopy analysis method for solving linear and nonlinear fractional diffusion-wave equation. Commun Nonlinear Sci Numer Simul 14:2006–2012
Kilbas AA, Trujillo JJ, Srivastava HM (2006) Theory and applications of fractional differential equations. Elsevier, Amsterdam
Langlands TAM, Henry BI, Wearne SL (2008) Anomalous subdiffusion with multispecies linear reaction dynamics. Phys Rev E 77:021111
Lenzi EK, Ribeiro HV, Tateishi AA, Zola RS, Evangelista LR (2016) Anomalous diffusion and transport in heterogeneous systems separated by a membrane. Proc R Soc A 472:20160502
Lukashchuk SY (2015) Conservation laws for time-fractional subdiffusion and diffusion-wave equations. Nonlinear Dyn 80:791–802
Ma WX (2012) A refined invariant subspace method and applications to evolution equations. Sci China Math 55:1769–1778
Ma WX, Liu Y (2012) Invariant subspaces and exact solutions of a class of dispersive evolution equations. Commun Nonlinear Sci Numer Simul 17:3795–3801
Ma WX, Zhang Y, Tang Y, Tu J (2012) Hirota bilinear equations with linear subspaces of solutions. Appl Math Comput 218:7174–7183
Mainardi F (1997) Fractional calculus: some basic problems in continuum and statistical mechanics. In: Carpinteri A, Mainardi F (eds) Fractals and fractional calculus in continuum mechanics. Springer, New York, pp 291–348
Metzler R, Klafter J (2000) The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys Rep 339:1–77
Murray JD (2002) Mathematical biology. Springer, New York
Nass AM (2019) Lie symmetry analysis and exact solutions of fractional ordinary differential equations with neutral delay. Appl Math Comput 347:370–380
Odibat Z, Momani S (2008) A generalized differential transform method for linear partial differential equations of fractional order. Appl Math Lett 21:194–199
Perumpanani AJ, Sherratt JA, Maini PK (1995) Phase differences in reaction-diffusion-advection systems and applications to morphogenesis. IMA J Appl Math 55:19–33
Podlubny I (1999) Fractional differential equations. Academic Press, New York
Povstenko YZ (2013) Fractional heat conduction in infinite one-dimensional composite medium. J Thermal Stresses 36:351–363
Povstenko Y (2015a) Fractional thermoelasticity. Springer, Bern
Povstenko Y (2015b) Linear fractional diffusion-wave equation for scientists and engineers. Birkhäuser, New York
Prakash P (2019) New exact solutions of generalized convection-reaction-diffusion equation. Eur Phys J Plus 134:261
Prakash P (2020) Invariant subspaces and exact solutions for some types of scalar and coupled time-space fractional diffusion equations. Pramana-J Phys 94:103
Prakash P (2021) On group analysis, conservation laws and exact solutions of time-fractional Kudryashov–Sinelshchikov equation. Comput Appl Math 40:162
Prakash P, Sahadevan R (2017) Lie symmetry analysis and exact solution of certain fractional ordinary differential equations. Nonlinear Dyn 89:305–319
Prakash P, Choudhary S, Daftardar-Gejji V (2020) Exact solutions of generalized time-fractional nonlinear reaction-diffusion equations with time delay. Eur. Phys. J. Plus 135:490
Prakash P, Priyendhu KS, Anjitha KM (2022a) Initial value problem for the (2 + 1)-dimensional time-fractional generalized convection-reaction-diffusion wave equation: invariant subspaces and exact solutions. Comput Appl Math 41:30
Prakash P, Priyendhu KS, Lakshmanan M (2022b) Invariant subspace method for \((m+1)\)-dimensional nonlinear time-fractional partial differential equations. Commun Nonlinear Sci Numer Simul 111:106436
Prakash P, Thomas R, Bakkyaraj T (2023) Invariant subspaces and exact solutions: (1+1) and (2+1)-dimensional generalized time-fractional thin-film equations. Comput Appl Math 42:97
Priyendhu KS, Prakash P, Lakshmanan M (2023) Invariant subspace method to the initial and boundary value problem of the higher dimensional nonlinear time-fractional PDEs. Commun Nonlinear Sci Numer Simul 122:107245
Qu C, Zhu C (2009) Classification of coupled systems with two-component nonlinear diffusion equations by the invariant subspace method. J Phys A Math Theor 42:475201
Rui W (2018) Idea of invariant subspace combined with elementary integral method for investigating exact solutions of time-fractional NPDEs. Appl Math Comput 339:158–171
Rui W (2022) Separation method of semi-fixed variables together with dynamical system method for solving nonlinear time-fractional PDEs with higher-order terms. Nonlinear Dyn 109:943–961
Rui W, Zhang H (2020) Separation variable method combined with integral bifurcation method for solving time-fractional reaction-diffusion models. Comput Appl Math 39:299
Rui W, Yang X, Chen F (2022) Method of variable separation for investigating exact solutions and dynamical properties of the time-fractional Fokker–Planck equation. Phys A 595:127068
Sahadevan R, Bakkyaraj T (2012) Invariant analysis of time-fractional generalized Burgers and Korteweg–de Vries equations. J Math Anal Appl 393:341–347
Sahadevan R, Bakkyaraj T (2015) Invariant subspace method and exact solutions of certain time-fractional nonlinear partial differential equations. Fract Calc Appl Anal 18:146–162
Sahadevan R, Prakash P (2016) Exact solution of certain time-fractional nonlinear partial differential equations. Nonlinear Dyn 85:659–673
Sahadevan R, Prakash P (2017a) On Lie symmetry analysis and invariant subspace methods of coupled time-fractional partial differential equations. Chaos Solitons Fractals 104:107–120
Sahadevan R, Prakash P (2017b) Exact solutions and maximal dimension of invariant subspaces of time fractional coupled nonlinear partial differential equations. Commun Nonlinear Sci Numer Simul 42:158–177
Sahadevan R, Prakash P (2019) Lie symmetry analysis and conservation laws of certain time fractional partial differential equations. Int J Dyn Syst Differ Equ 9:44–64
Sethukumarasamy K, Vijayaraju P, Prakash P (2021) On Lie symmetry analysis of certain coupled fractional ordinary differential equations. J Nonlinear Math Phys 28:219–241
Song J, Shen S, Jin Y, Zhang J (2013) New maximal dimension of invariant subspaces to coupled systems with two-component equations. Commun Nonlinear Sci Numer Simul 18:2984–2992
Sun HG, Zhang Y, Baleanu D, Chen W, Chen YQ (2018) A new collection of real world applications of fractional calculus in science and engineering. Commun Nonlinear Sci Numer Simul 64:213–231
Tarasov VE (2011) Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles. Fields and Media, Nonlinear Physical Science. Springer, Heidelberg
Tarasov VE (2013) Review of some promising fractional physical models. Int J Mod Phys B 27:1330005
Tarasov VE, Trujillo JJ (2013) Fractional power-law spatial dispersion in electrodynamics. Ann Phys 334:1–23
Turing AM (1952) The chemical basis of morphogenesis. Philos Trans R Soc Lond B 237:37–72
Xu J, Rui W, Tang W (2023) Method of separating variables combined with approach of dynamic system for investigating exact solutions of nonlinear time-fractional models. Math Methods Appl Sci 46:5770–5793
Ye Y, Ma WX, Shen S, Zhang D (2014) A class of third-order nonlinear evolution equations admitting invariant subspaces and associated reductions. J Nonlinear Math Phys 21:132–148
Zhu C, Qu C (2011) Maximal dimension of invariant subspaces admitted by nonlinear vector differential operators. J Math Phys 52:043507
Zhu C, Qu C (2016) Invariant subspaces of the two-dimensional nonlinear evolution equations. Symmetry 8:128
Acknowledgements
The authors wish to thank the anonymous referees for their constructive suggestions. The second author (K.S.P.) would like to thank the International Mathematical Union (IMU), Germany, for providing financial support in the form of IMU Breakout Graduate fellowship-2023 (IMU-BGF-2023-06).
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Kai Diethelm.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Prakash, P., Priyendhu, K.S. & Meenakshi, M. Invariant subspace method and exact solutions of the coupled system of time-fractional convection–reaction–diffusion equations. Comp. Appl. Math. 43, 30 (2024). https://doi.org/10.1007/s40314-023-02540-2
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-023-02540-2
Keywords
- Fractional PDEs
- Initial value problems
- Invariant subspace method
- Coupled system of fractional convection–reaction–diffusion equations
- Exact solutions