Skip to main content
Springer Nature Link
Log in

Convergence analysis for solving the split equality equilibrium problem in Hilbert spaces

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

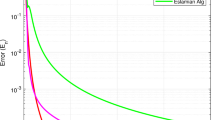
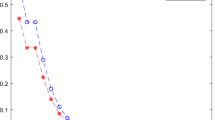
In this paper, we propose four alternated inertial algorithms with self-adaptive stepsize to address the split equality equilibrium problem (SEEP) in real Hilbert spaces, without the need for any prior knowledge of the operator norm. Moreover, these algorithms adopt the convex subset form by a sequence of closed balls rather than half-spaces, and it is simple to calculate the projections onto these sets. Under some proper assumptions, we demonstrate weak and strong convergence theorems of our algorithms, particularly strong convergence towards the minimum-norm solution of the SEEP. As application, we will utilize our results to study the split equality variational inequality problem. Finally, we provide a numerical example to illustrate the effectiveness of the proposed algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Algorithm 1
Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Data availability

The Matlab codes employed to run the numerical experiments are available upon request.

References

  • Anh PN (2013) A hybrid extragradient method extended to fixed point problems and equilibrium problems. Optimization 62(2):271–283

    MathSciNet  Google Scholar 

  • Ansari QH, Rehan A (2014) Split feasibility and fixed point problems. Nonlinear analysis, approximation theory, optimization and applications. Springer, Berlin, pp 281–322

  • Bauschke HH, Combettes PL (2001) A weak-to-strong convergence principle for Fejér-monotone methods in Hilbert spaces. Math Oper Res 26(2):248–264

    MathSciNet  Google Scholar 

  • Bauschke HH, Combettes PL (2011) Convex analysis and monotone operator theory in Hilbert spaces. Springer, Berlin

    Google Scholar 

  • Blum E, Oettli W (1994) From optimization and variational inequalities to equilibrium problems. Math Stud 63:123–145

    MathSciNet  Google Scholar 

  • Bnouhachem A, Suliman AH, Ansari QH (2014) An iterative method for common solution of equilibrium problems and hierarchical fixed point problems. Fixed Point Theory Appl 1:1–21

    MathSciNet  Google Scholar 

  • Byrne CL (2002) Iterative oblique projection onto convex sets and the split feasibility problem. Inverse Probl 18(2):441–453

    MathSciNet  Google Scholar 

  • Byrne C (2004) A unified treatment for some iterative algorithms in signal processing and image reconstruction. Inverse Probl 20(1):103–120

    MathSciNet  Google Scholar 

  • Censor Y, Elfving T (1994) A multiprojection algorithm using Bregman projections in a product space. Numer Algorithms 8:221–239

    MathSciNet  Google Scholar 

  • Censor Y, Bortfeld T, Martin B, Trofimov A (2006) A unified approach for inversion problems in intensity modulated radiation therapy. Phys Med Biol 51(10):2353–2365

    Google Scholar 

  • Chang SS, Lee HWJ, Chan CK (2009) A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Anal 70(9):3307–3319

    MathSciNet  Google Scholar 

  • Combettes PL, Hirstoaga SA (2005) Equilibrium programming in Hilbert spaces. J Nonlinear Convex Anal 6(1):117–136

    MathSciNet  Google Scholar 

  • Dang Y, Sun J, Xu H (2017) Inertial accelerated algorithms for solving a split feasibility problem. J Ind Manag Optim 13(3):1383–1394

    MathSciNet  Google Scholar 

  • Dang Y, Sun J, Zhang S (2019) Double projection algorithms for solving the split feasibility problems. J Ind Manag Optim 15(4):2023–2034

    MathSciNet  Google Scholar 

  • Dong QL, Jiang D (2017) Solve the split equality problem by a projection algorithm with inertial effects. J Nonlinear Sci Appl 10(3):1244–1251

    MathSciNet  Google Scholar 

  • Dong QL, He S, Zhao J (2015) Solving the split equality problem without prior knowledge of operator norms. Optimization 64(9):1887–1906

    MathSciNet  Google Scholar 

  • Dong QL, He S, Rassias MT (2021) General splitting methods with linearization for the split feasibility problem. J Global Optim 79(4):813–836

    MathSciNet  Google Scholar 

  • Eslamian M (2013) Hybrid method for equilibrium problems and fixed point problems of finite families of nonexpansive semigroups. RACSAM 107(2):299–307

    MathSciNet  Google Scholar 

  • Eslamian M, Abkar A (2014) Viscosity iterative scheme for generalized mixed equilibrium problems and nonexpansive semigroups. TOP 22:554–570

    MathSciNet  Google Scholar 

  • Flam DS, Antipin AS (1997) Equilibrium programming using proximal-like algorithms. Math Program 78(1):29–41

    MathSciNet  Google Scholar 

  • Gibali A, Mai DT, Vinh NT (2019) A new relaxed CQ algorithm for solving split feasibility problems in Hilbert spaces and its applications. J Ind Manag Optim 15(2):963–984

    MathSciNet  Google Scholar 

  • He S, Yang C (2013) Solving the variational inequality problem defined on intersection of finite level sets. Abstr Appl Anal 2013:942315

    MathSciNet  Google Scholar 

  • Iiduka H, Yamada I (2009) A use of conjugate gradient direction for the convex optimization problem over the fixed point set of a nonexpansive mapping. SIAM J Optim 19(4):1881–1893

    MathSciNet  Google Scholar 

  • Jouymandi Z, Moradlou F (2019) Extragradient and linesearch methods for solving split feasibility problems in Hilbert spaces. Math Methods Appl Sci 42(12):4343–4359

    MathSciNet  Google Scholar 

  • Kazmi KR, Rizvi SH (2014) An iterative method for split variational inclusion problem and fixed point problem for a nonexpansive mapping. Optim Lett 8(3):1113–1124

    MathSciNet  Google Scholar 

  • Kesornprom S, Pholasa N, Cholamjiak P (2020) On the convergence analysis of the gradient-CQ algorithms for the split feasibility problem. Numer Algorithms 84(3):997–1017

    MathSciNet  Google Scholar 

  • Li HY, Wu YL, Wang FH (2022) Convergence analysis for solving equilibrium problems and split feasibility problems in Hilbert spaces. Optimization 72(7):1863–1898

    MathSciNet  Google Scholar 

  • López G, Martín-Márquez V, Wang F, Xu HK (2012) Solving the split feasibility problem without prior knowledge of matrix norms. Inverse Probl 28(8):085004

    MathSciNet  Google Scholar 

  • Ma ZL, Wang L, Chang S, Duan W (2015) Convergence theorems for split equality mixed equilibrium problems with applications. Fixed Point Theory Appl 1:1–18

    MathSciNet  Google Scholar 

  • Maingé PE (2008) A hybrid extragradient-viscosity method for monotone operators and fixed point problems. SIAM J Control Optim 47(3):1499–1515

    MathSciNet  Google Scholar 

  • Moudafi A (2003) Second-order differential proximal methods for equilibrium problems. J Inequal Pure Appl Math 4(1):1–7

    MathSciNet  Google Scholar 

  • Moudafi A (2013a) Alternating CQ-algorithm for convex feasibility and split fixed-point problems. J Nonlinear Convex Anal 15(4):809–818

  • Moudafi A (2013b) A relaxed alternating CQ-algorithm for convex feasibility problems. Nonlinear Anal Theory Methods Appl 79:117–121

  • Moudafi A, Gibali A (2018) \(l_1-l_2\) regularization of split feasibility problems. Numer Algorithms 78(3):739–757

    MathSciNet  Google Scholar 

  • Mu Z, Peng Y (2015) A note on the inertial proximal point method. Stat Optim Inf Comput 3(3):241–248

    MathSciNet  Google Scholar 

  • Opial Z (1967) Weak convergence of the sequence of successive approximations for nonexpensive mappings. Bull Am Math Soc 73(4):591–597

    Google Scholar 

  • Polyak BT (1964) Some methods of speeding up the convergence of iteration methods. USSR Comput Math Math Phys 4(5):1–17

    Google Scholar 

  • Qin X, Shang M, Su Y (2008) A general iterative method for equilibrium problems and fixed point problems in Hilbert spaces. Nonlinear Anal 69(11):3897–3909

    MathSciNet  Google Scholar 

  • Shehu Y, Gibali A (2021) New inertial relaxed method for solving split feasibilities. Optim Lett 15(6):2109–2126

    MathSciNet  Google Scholar 

  • Shehu Y, Dong QL, Liu L (2021) Global and linear convergence of alternated inertial methods for split feasibility problems. RACSAM 115:1–26

    MathSciNet  Google Scholar 

  • Xu HK (2002) Iterative algorithms for nonlinear operators. J Lond Math Soc 66(1):240–256

    MathSciNet  Google Scholar 

  • Xu HK (2010) Iterative methods for the split feasibility problem in infinite dimensional Hilbert spaces. Inverse Probl 26(10):105018

    MathSciNet  Google Scholar 

  • Yang Q (2004) The relaxed CQ algorithm solving the split feasibility problem. Inverse Probl 20(4):1261–1266

    MathSciNet  Google Scholar 

  • Yao Y, Cho YJ, Liou YC (2010) Iterative algorithm for hierarchical fixed points problems and variational inequalities. Math Comput Model 52(9–10):1697–1705

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Tiangong University, Tianjin, 300387, China

    Yishuo Peng, Yu Cao & Yasong Chen

  2. School of Software, Tiangong University, Tianjin, 300387, China

    Luoyi Shi

Authors
  1. Yishuo Peng
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yu Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Luoyi Shi
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yasong Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yasong Chen.

Ethics declarations

Conflict of interest

The authors declare no conflicts of interest.

Additional information

Communicated by Baisheng Yan.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Peng, Y., Cao, Y., Shi, L. et al. Convergence analysis for solving the split equality equilibrium problem in Hilbert spaces. Comp. Appl. Math. 43, 111 (2024). https://doi.org/10.1007/s40314-024-02618-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-024-02618-5

Keywords

Mathematics Subject Classification