Skip to main content
Springer Nature Link
Log in

An efficient data assimilation based unconditionally stable scheme for Cahn–Hilliard equation

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

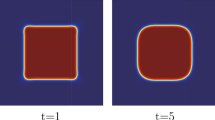
Abstract

This paper aims to present an efficient numerical method for solving the Cahn–Hilliard equation incorporating a data assimilation term. The data assimilation term employs a feedback control strategy to guide the computational solution towards the observed data. The Crank–Nicolson formula is employed for discretizing the equation system, while a scalar auxiliary variable approach is adopted to ensure energy dissipation preservation. The proposed scheme attains second-order accuracy in both temporal and spatial dimensions. The unconditional energy stability of the scheme is proven theoretically. Numerous numerical experiments are conducted to illustrate the efficacy of the proposed scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Availability of data and materials

The data used in this paper are available at https://github.com/xjtu-songxin/dataset-for-CH-equation-with-data-assimilation-method.git.

References

  • Agosti A, Antonietti PF, Ciarletta P, Grasselli M, Verani M (2017) A Cahn–Hilliard-type equation with application to tumor growth dynamics. Math Methods App Sci 40(18):7598–7626

    MathSciNet  Google Scholar 

  • Albanez DA, Benvenutti MJ (2018) Continuous data assimilation algorithm for simplified Bardina model. Evol Equ Control Theory 7(1):33

    MathSciNet  Google Scholar 

  • Albanez DA, Nussenzveig Lopes HJ, Titi ES (2016) Continuous data assimilation for the three-dimensional Navier–Stokes-\(\alpha \) model. Asymptot Anal 97(1–2):139–164

    MathSciNet  Google Scholar 

  • Anthes RA (1974) Data assimilation and initialization of hurricane prediction models. J Atmos Sci 31(3):702–719

    Google Scholar 

  • Azouani A, Titi ES (2013) Feedback control of nonlinear dissipative systems by finite determining parameters-a reaction-diffusion paradigm. arXiv preprint arXiv:1301.6992

  • Azouani A, Olson E, Titi ES (2014) Continuous data assimilation using general interpolant observables. J Nonlinear Sci 24(2):277–304

    MathSciNet  Google Scholar 

  • Badalassi VE, Ceniceros HD, Banerjee S (2003) Computation of multiphase systems with phase field models. J Comput Phys 190(2):371–397

    MathSciNet  Google Scholar 

  • Cahn JW (1961) On spinodal decomposition. Acta Metall 9(9):795–801

    Google Scholar 

  • Cahn JW, Hilliard JE (1958) Free energy of a nonuniform system. I. Interfacial free energy. J Chem Phys 28(2):258–267

    Google Scholar 

  • Carlson E, Hudson J, Larios A (2020) Parameter recovery for the 2 dimensional Navier–Stokes equations via continuous data assimilation. SIAM J Sci Comput 42(1):250–270

    MathSciNet  Google Scholar 

  • Chen W, Feng W, Liu Y, Wang C, Wise SM (2016) A second order energy stable scheme for the Cahn–Hilliard–Hele–Shaw equations. arXiv preprint arXiv:1611.02967

  • Cheng K, Wang C, Wise SM (2020) A weakly nonlinear, energy stable scheme for the strongly anisotropic Cahn–Hilliard equation and its convergence analysis. J Comput Phys 405:109109

    MathSciNet  Google Scholar 

  • Elliott CM, Stuart AM (1993) The global dynamics of discrete semilinear parabolic equations. SIAM J Numer Anal 30(6):1622–1663. https://doi.org/10.1137/0730084

    Article  MathSciNet  Google Scholar 

  • Foias C, Temam R (1984) Determination of the solutions of the Navier–Stokes equations by a set of nodal values. Math Comput 43(167):117–133

    MathSciNet  Google Scholar 

  • Foias C, Mondaini CF, Titi ES (2016) A discrete data assimilation scheme for the solutions of the two-dimensional Navier–Stokes equations and their statistics. SIAM Jo Appl Dyn Syst 15(4):2109–2142

    MathSciNet  Google Scholar 

  • Gao Y, Li R, He X, Lin Y (2024) A fully decoupled numerical method for Cahn–Hilliard–Navier–Stokes–Darcy equations based on auxiliary variable approaches. J Comput Appl Math 436:115363

    MathSciNet  Google Scholar 

  • Guillén-González F, Tierra G (2013) On linear schemes for a Cahn–Hilliard diffuse interface model. J Comput Phys 234:140–171. https://doi.org/10.1016/j.jcp.2012.09.020

    Article  MathSciNet  Google Scholar 

  • He Y, Chen H (2022) Efficient algorithm and convergence analysis of conservative sav compact difference scheme for Boussinesq paradigm equation. Comput Math Appl 125:34–50

    MathSciNet  Google Scholar 

  • He Y, Chen H (2022) Efficient and conservative compact difference scheme for the coupled Schrödinger–Boussinesq equations. Appl Numer Math 182:285–307

    MathSciNet  Google Scholar 

  • Jolly MS, Martinez VR, Titi ES (2017) A data assimilation algorithm for the subcritical surface quasi-geostrophic equation. Adv Nonlinear Stud 17(1):167–192

    MathSciNet  Google Scholar 

  • Ju L, Li X, Qiao Z (2022) Generalized sav-exponential integrator schemes for Allen–Cahn type gradient flows. SIAM J Numer Anal 60(4):1905–1931

    MathSciNet  Google Scholar 

  • Kalman RE (1960) A new approach to linear filtering and prediction problems. J Basic Eng 82(1):35–45. https://doi.org/10.1115/1.3662552 (https://asmedigitalcollection.asme.org/fluidsengineering/article-pdf/82/1/35/5518977/35_1.pdf)

    Article  MathSciNet  Google Scholar 

  • Kelly DT, Law KJ, Stuart AM (2014) Well-posedness and accuracy of the ensemble Kalman filter in discrete and continuous time. Nonlinearity 27(10):2579

    MathSciNet  Google Scholar 

  • Kotschote M, Zacher R (2015) Strong solutions in the dynamical theory of compressible fluid mixtures. Math Models Methods Appl Sci 25(07):1217–1256

    MathSciNet  Google Scholar 

  • Lee C, Jeong D, Shin J, Li Y, Kim J (2014) A fourth-order spatial accurate and practically stable compact scheme for the Cahn–Hilliard equation. Physica A 409:17–28

    MathSciNet  Google Scholar 

  • Li Y, Kim J (2012) A comparison study of phase-field models for an immiscible binary mixture with surfactant. Eur Phys J B 85:1–9

    Google Scholar 

  • Li X, Shen J (2020) Error analysis of the sav-mac scheme for the Navier–Stokes equations. SIAM J Numer Anal 58(5):2465–2491

    MathSciNet  Google Scholar 

  • Li X, Shen J, Rui H (2019) Energy stability and convergence of sav block-centered finite difference method for gradient flows. Math Comput 88(319):2047–2068

    MathSciNet  Google Scholar 

  • Li Y, Liu R, Xia Q, He C, Li Z (2022) First-and second-order unconditionally stable direct discretization methods for multi-component Cahn–Hilliard system on surfaces. J Comput Appl Math 401:113778

    MathSciNet  Google Scholar 

  • Maraldi M, Molari L, Grandi D (2012) A unified thermodynamic framework for the modelling of diffusive and displacive phase transitions. Int J Eng Sci 50(1):31–45

    MathSciNet  Google Scholar 

  • Markowich PA, Titi ES, Trabelsi S (2016) Continuous data assimilation for the three-dimensional Brinkman–Forchheimer-extended Darcy model. Nonlinearity 29(4):1292

    MathSciNet  Google Scholar 

  • Meng X, Bao X, Zhang Z (2023) Second order stabilized semi-implicit scheme for the Cahn–Hilliard model with dynamic boundary conditions. J Comput Appl Math 428:115145

    MathSciNet  Google Scholar 

  • Pawar S, Ahmed SE, San O, Rasheed A, Navon IM (2020) Long short-term memory embedded nudging schemes for nonlinear data assimilation of geophysical flows. Phys Fluids 32(7):076606

    Google Scholar 

  • Robert C, Durbiano S, Blayo E, Verron J, Blum J, Le Dimet F-X (2005) A reduced-order strategy for 4d-var data assimilation. J Mar Syst 57(1–2):70–82

    Google Scholar 

  • Sasaki K, Yamanaka A, Ito S-I, Nagao H (2018) Data assimilation for phase-field models based on the ensemble Kalman filter. Comput Mater Sci 141:141–152

    Google Scholar 

  • Shen J, Xu J, Yang J (2018) The scalar auxiliary variable (sav) approach for gradient flows. J Comput Phys 353:407–416. https://doi.org/10.1016/j.jcp.2017.10.021

    Article  MathSciNet  Google Scholar 

  • Sugiura N, Awaji T, Masuda S, Mochizuki T, Toyoda T, Miyama T, Igarashi H, Ishikawa Y (2008) Development of a four-dimensional variational coupled data assimilation system for enhanced analysis and prediction of seasonal to interannual climate variations. J Geophys Res 113:C10017

    Google Scholar 

  • Wang H, Sun J, Zhang X, Huang X-Y, Auligné T (2013) Radar data assimilation with wrf 4d-var. Part I: system development and preliminary testing. Mon Weather Rev 141(7):2224–2244

    Google Scholar 

  • Weaver AT, Vialard J, Anderson DLT (2003) Three- and four-dimensional variational assimilation with a general circulation model of the tropical pacific ocean. Part I: formulation, internal diagnostics, and consistency checks. Mon Weather Rev 131:1360–1378

    Google Scholar 

  • Wise SM, Lowengrub JS, Frieboes HB, Cristini V (2008) Three-dimensional multispecies nonlinear tumor growth—I: model and numerical method. J Theor Biol 253(3):524–543

    MathSciNet  Google Scholar 

  • Xia Q, Kim J, Li Y (2022) Modeling and simulation of multi-component immiscible flows based on a modified Cahn–Hilliard equation. Eur J Mech B Fluids 95:194–204

    MathSciNet  Google Scholar 

  • Xia B, Yu R, Song X, Zhang X, Kim J (2023) An efficient data assimilation algorithm using the Allen–Cahn equation. Eng Anal Bound Elem 155:511–517

    MathSciNet  Google Scholar 

  • Xia Q, Liu Y, Kim J, Li Y (2023) Binary thermal fluids computation over arbitrary surfaces with second-order accuracy and unconditional energy stability based on phase-field model. J Comput Appl Math 433:115319

    MathSciNet  Google Scholar 

  • Yamamura A, Sakane S, Ohno M, Yasuda H, Takaki T (2022) Data assimilation with phase-field lattice Boltzmann method for dendrite growth with liquid flow and solid motion. Comput Mater Sci 215:111776

    Google Scholar 

  • Yang X (2016) Linear, first and second-order, unconditionally energy stable numerical schemes for the phase field model of homopolymer blends. J Comput Phys 327:294–316. https://doi.org/10.1016/j.jcp.2016.09.029

    Article  MathSciNet  Google Scholar 

  • Zhang C, Ouyang J, Wang C, Wise SM (2020) Numerical comparison of modified-energy stable sav-type schemes and classical bdf methods on benchmark problems for the functionalized cahn-hilliard equation. J Comput Phys 423:109772

    MathSciNet  Google Scholar 

  • Zhu G, Chen H, Yao J, Sun S (2019) Efficient energy-stable schemes for the hydrodynamics coupled phase-field model. Appl Math Model 70:82–108

    MathSciNet  Google Scholar 

  • Zhu G, Kou J, Yao J, Li A, Sun S (2020) A phase-field moving contact line model with soluble surfactants. J Comput Phys 405:109170

    MathSciNet  Google Scholar 

Download references

Acknowledgements

This work is supported by National Natural Science Foundation of China (No. 12271430) and Scientific Research Fund for High-level Talents of Xijing University (No. XJ23B08). The authors would like to thank the reviewers for their constructive and helpful comments regarding the revision of this article.

Funding

This work is supported by Natural Science Basic Research Program of Shaanxi (No. 2024JC-YBMS-016) and by Scientific Research Fund for High-level Talents of Xijing University (No. XJ23B08).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xi’an Jiaotong University, No. 28 Xianning West Road, Xi’an, 710049, Shannxi, China

    Xin Song & Yibao Li

  2. School of Computer Science, Xijing University, Xi’an, 710049, Shannxi, China

    Binhu Xia

Authors
  1. Xin Song
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Binhu Xia
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Yibao Li
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Not applicable.

Corresponding author

Correspondence to Yibao Li.

Ethics declarations

Conflict of interest

Conflict of interest The authors declare that they have no Conflict of interest.

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Code availability

Not applicable.

Additional information

Communicated by Carlos Conca.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, X., Xia, B. & Li, Y. An efficient data assimilation based unconditionally stable scheme for Cahn–Hilliard equation. Comp. Appl. Math. 43, 121 (2024). https://doi.org/10.1007/s40314-024-02632-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-024-02632-7

Keywords

Mathematics Subject Classification