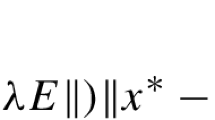Skip to main content
Springer Nature Link
Log in

New iterative methods for solving generalized absolute value equations

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

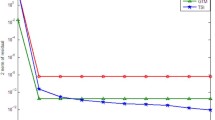
In this paper, two new iterative methods for solving generalized absolute value equations (GAVEs) are proposed and investigated using the single-step iteration (SSI) approach. The proposed iterative methods are Picard-SSI and nonlinear SSI-like methods. In the implementation of the Picard-SSI method, we have used the SSI method as an inner solver. The convergence of the proposed method for solving GAVE is analyzed under reasonable constraints. Several numerical examples are given to illustrate the efficiency and implementation of the proposed methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Data Availability

No new data was created in this work.

References

  • Bai Z-Z (1997) A class of two-stage iterative methods for systems of weakly nonlinear equations. Numer Algorithms 14:295–319

    Article  MathSciNet  Google Scholar 

  • Bai Z-Z (2010) Modulus-based matrix splitting iteration methods for linear complementarity problems. Numer Linear Algebra Appl 17(6):917–933

    Article  MathSciNet  Google Scholar 

  • Bai Z-Z, Yang X (2009) On HSS-based iteration methods for weakly nonlinear systems. Appl Numer Math 59(12):2923–2936

    Article  MathSciNet  Google Scholar 

  • Bai Z-Z, Golub GH, Ng MK (2003) Hermitian and skew-Hermitian splitting methods for non-Hermitian positive definite linear systems. SIAM J Matrix Anal Appl 24(3):603–626

    Article  MathSciNet  Google Scholar 

  • Benzi M (2009) A generalization of the Hermitian and skew-Hermitian splitting iteration. SIAM J Matrix Anal Appl 31(2):360–374

    Article  MathSciNet  Google Scholar 

  • Cottle RW, Pang J-S, Stone RE (1992) The linear complementarity problem. Academic Press, San Diego

    Google Scholar 

  • Dehghan M, Shirilord A (2020) Matrix multisplitting Picard-iterative method for solving generalized absolute value matrix equation. Appl Numer Math 158:425–438

    Article  MathSciNet  Google Scholar 

  • Dong X, Shao X-H, Shen H-L (2020) A new SOR-like method for solving absolute value equations. Appl Numer Math 156:410–421

    Article  MathSciNet  Google Scholar 

  • Ebadi G, Alipour N, Vuik C (2016) Deflated and augmented global Krylov subspace methods for the matrix equations. Appl Numer Math 99:137–150

    Article  MathSciNet  Google Scholar 

  • Golub GH, Van Loan CF (2013) Matrix computations. Johns Hopkins University Press, Baltimore

    Book  Google Scholar 

  • Idema R, Vuik C (2023) A comparison of Krylov methods for shifted skew-symmetric systems. https://doi.org/10.48550/arXiv.2304.04092

  • Li C-X, Wu S-L (2012) A modified GHSS method for non-Hermitian positive definite linear systems. Jpn J Ind Appl Math 29(2):253–268

    Article  MathSciNet  Google Scholar 

  • Li C-X, Wu S-L (2015) A single-step HSS method for non-Hermitian positive definite linear systems. Appl Math Lett 44:26–29

    Article  MathSciNet  Google Scholar 

  • Li X, Li Y-X, Dou Y (2023) Shift-splitting fixed point iteration method for solving generalized absolute value equations. Numer Algorithms 93:695–710

    Article  MathSciNet  Google Scholar 

  • Mangasarian OL (2009) A generalized Newton method for absolute value equations. Optim Lett 3:101–108

    Article  MathSciNet  Google Scholar 

  • Mangasarian OL, Meyer RR (2006) Absolute value equations. Linear Algebra Appl 419:359–367

    Article  MathSciNet  Google Scholar 

  • Miao S-X, Zhang J (2020) On Uzawa-SSI method for non-Hermitian saddle point problems. AIMS Math 5(6):7301–7315

    Article  MathSciNet  Google Scholar 

  • Miao S-X, Xiong X-T, Wen J (2021) On Picard-SHSS iteration method for absolute value equation. AIMS Math 6(2):1743–1753

    Article  MathSciNet  Google Scholar 

  • Murty KG, Yu FT (1998) Linear complementarity, linear and nonlinear programming, vol 3. Heldermann, Berlin

    Google Scholar 

  • Noor MA, Noor KI, Batool S (2018) On generalized absolute value equations. UPB Sci Bull Ser A Appl Math Phys 80(4):63–70

    MathSciNet  Google Scholar 

  • Ortega JM, Rheinbolt WC (1970) Iterative solution of nonlinear equations in several variables. Academic Press, New York

    Google Scholar 

  • Prokopyev O (2009) On equivalent reformulations for absolute value equations. Comput Optim Appl 44:363–372

    Article  MathSciNet  Google Scholar 

  • Rohn J (2004) A theorem of the alternatives for the equation \(Ax + B| x | = b\). Linear Multilinear Algebra 52(6):421–426

    Article  MathSciNet  Google Scholar 

  • Rohn J (2009) On unique solvability of the absolute value equation. Optim Lett 3:603–606

    Article  MathSciNet  Google Scholar 

  • Salkuyeh DK (2014) The Picard-HSS iteration method for absolute value equations. Optim Lett 8:2191–2202

    Article  MathSciNet  Google Scholar 

  • Seifollahzadeh S, Ebadi G (2024) On diagonal and off-diagonal splitting-based iteration method to solve absolute value equations. Filomat 38(6):2001–2013

    MathSciNet  Google Scholar 

  • Trefethen LN, Bau D (1997) Numerical linear algebra. SIAM, Philadelphia

    Book  Google Scholar 

  • Wang A, Cao Y, Chen J-X (2019) Modified Newton-type iteration methods for generalized absolute value equations. J Optim Theory Appl 181:216–230

    Article  MathSciNet  Google Scholar 

  • Wang X, Xiao X-Y, Zheng Q-Q (2019) A single-step iteration method for non-Hermitian positive definite linear systems. J Comput Appl Math 346:471–482

    Article  MathSciNet  Google Scholar 

  • Wu S-L, Li C-X (2020) A note on unique solvability of the absolute value equation. Optim Lett 14(7):1957–1960

    Article  MathSciNet  Google Scholar 

  • Wu Y-J, Li X, Yuan J-Y (2017) A non-alternating preconditioned HSS iteration method for non-Hermitian positive definite linear systems. Comput Appl Math 36(1):367–381

    Article  MathSciNet  Google Scholar 

  • Wu Y-J, Zhang W-H, Yang A-L (2022) Modulus-based inexact non-alternating preconditioned splitting method for linear complementarity problems. Linear Multilinear Algebra 70(22):7414–7432

    Article  MathSciNet  Google Scholar 

  • Yong L (2015) Iteration method for absolute value equation and applications in two-point boundary value problem of linear differential equation. J Interdiscip Math 18:355–374

    Article  Google Scholar 

  • Zhang J-J (2015) The relaxed nonlinear PHSS-like iteration method for absolute value equations. Appl Math Comput 265:266–274

    MathSciNet  Google Scholar 

  • Zhou H-Y, Wu S-L, Li C-X (2021) Newton-based matrix splitting method for generalized absolute value equation. J Comput Appl Math 394:113578

    Article  MathSciNet  Google Scholar 

  • Zhu M-Z, Qi Y-E (2018) The nonlinear HSS-like iteration method for absolute value equations. IAENG Int J Appl Math 48(3):75–79

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of mathematics, Statistics and Computer Science, University of Tabriz, Tabriz, Iran

    Ghodrat Ebadi & Somayeh Seifollahzadeh

  2. Institute of Applied Mathematics, Delft University of Technology, Delft, The Netherlands

    Cornelis Vuik

Authors
  1. Ghodrat Ebadi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Somayeh Seifollahzadeh
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Cornelis Vuik
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Ghodrat Ebadi.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ebadi, G., Seifollahzadeh, S. & Vuik, C. New iterative methods for solving generalized absolute value equations. Comp. Appl. Math. 43, 313 (2024). https://doi.org/10.1007/s40314-024-02811-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-024-02811-6

Keywords

Mathematics Subject Classification