Skip to main content
Springer Nature Link
Log in

Computational study based on the Laplace transform and local discontinuous Galerkin methods for solving fourth-order time-fractional partial integro-differential equations with weakly singular kernels

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

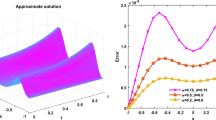
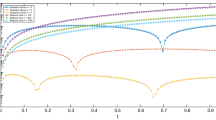
The aim of this paper is to implement the high-order local discontinuous Galerkin method (LDGM) for solving partial integro-differential equations (PIDEs) in two dimensions. Time marching method and the transform-based method known as the non-time marching method can be used to discretize temporal terms. The combination of a small time step size in time marching methods and a high-order scheme in space with many degrees of freedom requires a considerable amount of computational time. In order to address this limitation, we propose an algorithm based on a combination of the Laplace transform and LDGM for solving fourth-order time-fractional (TF) PIDEs with weakly singular kernels. Unlike time-marching approaches, the transform-based method has a much lower computational complexity and can take advantage of parallel computing. A numerical experiment validates the accuracy and applicability of the proposed temporal discretization approach and also shows that k-degree LDG solutions have a \(k + 1\) convergence rate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Data Availability

No new data were created or analyzed during this study. Data sharing is not applicable to this article.

References

  • Abbaszadeh M, Dehghan M (2021) A finite-difference procedure to solve weakly singular integro partial differential equation with space-time fractional derivatives. Eng. Comput. 37(3):2173–2182

    Google Scholar 

  • Abbaszadeh M, Dehghan M, Zhou Y (2020) Crank-Nicolson/Galerkin spectral method for solving two-dimensional time-space distributed-order weakly singular integro-partial differential equation. J. Comput. Appl. Math. 374:112739

    MathSciNet  Google Scholar 

  • Ahmadinia M, Safari Z, Fouladi S (2018) Analysis of local discontinuous Galerkin method for time-space fractional convection-diffusion equations. BIT Numer. Math. 58(3):533–554

    MathSciNet  Google Scholar 

  • Alipanah A, Esmaeili S (2011) Numerical solution of the two-dimensional Fredholm integral equations using Gaussian radial basis function. J. Comput. Appl. Math. 235(18):5342–5347

    MathSciNet  Google Scholar 

  • Assari P (2019) On the numerical solution of two-dimensional integral equations using a meshless local discrete Galerkin scheme with error analysis. Eng. Comput. 35(3):893–916

    MathSciNet  Google Scholar 

  • Assari P, Asadi-Mehregan F (2019) Local radial basis function scheme for solving a class of fractional integro-differential equations based on the use of mixed integral equations. ZAMM- J. Appl. Math. Mech. 99(8):e201800236

    MathSciNet  Google Scholar 

  • Assari P, Cuomo S (2019) The numerical solution of fractional differential equations using the Volterra integral equation method based on thin plate splines. Eng. Comput. 35(4):1391–1408

    Google Scholar 

  • Assari P, Dehghan M (2019) Application of dual-Chebyshev wavelets for the numerical solution of boundary integral equations with logarithmic singular kernels. Eng. Comput. 35(1):175–190

    Google Scholar 

  • Baccouch M (2020) A superconvergent local discontinuous Galerkin method for nonlinear fourth-order boundary-value problems. Int. J. Comput. Methods. 17(07):1950035

    MathSciNet  Google Scholar 

  • Baccouch M, Temimi H, Ben-Romdhane M (2019) Optimal error estimates and superconvergence of an ultra weak discontinuous Galerkin method for fourth-order boundary-value problems. Appl. Numer. Math. 137:91–115

    MathSciNet  Google Scholar 

  • Ciarlet PG, Raviart PA (1974) A mixed finite element method for the biharmonic equation. In: de Boor C (ed) Mathematical Aspects of Finite Elements in Partial Differential Equations. Academic Press, New York, pp 125–145

    Google Scholar 

  • Cockburn B, Dong B (2007) An analysis of the minimal dissipation local discontinuous Galerkin method for convection-diffusion problems. J. Sci. Comput. 32(2):233–262

    MathSciNet  Google Scholar 

  • Cockburn B, Shu C-W (1998) The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 35(6):2440–2463

    MathSciNet  Google Scholar 

  • Dehghan M (2006) Solution of a partial integro-differential equation arising from viscoelasticity. Int. J. Comput. Math. 83(1):123–129

    MathSciNet  Google Scholar 

  • Dehghan M, Abbaszadeh M (2019) Error estimate of finite element/finite difference technique for solution of two-dimensional weakly singular integro-partial differential equation with space and time fractional derivatives. J. Comput. Appl. Math. 356:314–328

    MathSciNet  Google Scholar 

  • Dehghan M, Manafian J, Saadatmandi A (2010) Solving nonlinear fractional partial differential equations using the homotopy analysis method. Numer. Methods Partial Differ. Equ. 26(2):448–479

    MathSciNet  Google Scholar 

  • Deng W, Hesthaven JS (2013) Local Discontinuous Galerkin methods for fractional diffusion equations, ESAIM: Math. Model. Numer. Anal. 47(6):1845–1864

    MathSciNet  Google Scholar 

  • Deng W, Hesthaven JS (2015) Local discontinuous Galerkin methods for fractional ordinary differential equations. BIT Numer. Math. 55(4):967–985

    MathSciNet  Google Scholar 

  • Dong B, Shu C-W (2009) Analysis of a local discontinuous Galerkin method for linear time-dependent fourth-order problems. SIAM J. Numer. Anal. 47(5):3240–3268

    MathSciNet  Google Scholar 

  • Engel G, Garikipati K, Hughes TJR, Larson MG, Mazzei L, Taylor RL (2002) Continuous/discontinuous finite element approximations of fourth-order elliptic problems in structural and continuum mechanics with applications to thin beams and plates, and strain gradient elasticity. Comput. Methods Appl. Mech. Eng. 191:3669–3750

    MathSciNet  Google Scholar 

  • Engström C, Giani S, Grubišić L (2023) Numerical solution of distributed-order time-fractional diffusion-wave equations using Laplace transforms. J. Comput. Appl. Math. 425:115035

    MathSciNet  Google Scholar 

  • Esmaeili S, Shamsi M, Luchko Y (2011) Numerical solution of fractional differential equations with a collocation method based on Müntz polynomials. Comput. Math. Appl. 62(3):918–929

    MathSciNet  Google Scholar 

  • Fakhar-Izadi F (2022) Fully spectral-Galerkin method for the one-and two-dimensional fourth-order time-fractional partial integro-differential equations with a weakly singular kernel. Numer. Methods Partial Differ. Equ. 38(2):160–176

    MathSciNet  Google Scholar 

  • Fakhar-Izadi F, Dehghan M (2016) Space-time spectral method for a weakly singular parabolic partial integro-differential equation on irregular domains. Comput. Math. Appl. 67(10):1884–1904

    MathSciNet  Google Scholar 

  • Fakhar-Izadi F, Dehghan M (2018) Fully spectral collocation method for nonlinear parabolic partial integro-differential equations. Appl. Numer. Math. 123:99–120

    MathSciNet  Google Scholar 

  • Fouladi S, Dahaghin MS (2022) Numerical investigation of the variable-order fractional Sobolev equation with non-singular Mittag-Leffler kernel by finite difference and local discontinuous Galerkin methods. Chaos, Solitons & Fractals. 157:111915

    MathSciNet  Google Scholar 

  • Fouladi S, Mohammadi-Firouzjaei H (2023) Local discontinuous Galerkin method for the Riesz space distributed-order Sobolev equation. Eng. Anal. Bound. Elem. 155:38–47

    MathSciNet  Google Scholar 

  • Fouladi S, Kohandel M, Eastman B (2022) A comparison and calibration of integer and fractional-order models of COVID-19 with stratified public response. Math. Biosci. Eng. 19(12):12792–12813

    MathSciNet  Google Scholar 

  • Giani S, Engström C, Grubišić L (2023) khp-adaptive spectral projection based discontinuous Galerkin method for the numerical solution of wave equations with memory. J. Comput. Appl. Math. 429:2023

    MathSciNet  Google Scholar 

  • Hannsgen KB, Wheeler RL (1984) Uniform \( L^{1} \) behavior in classes of integro-differential equations with completely monotonic kernels. SIAM J. Numer. Anal. 15(3):579–594

    Google Scholar 

  • Javidi M, Ahmad B (2015) Numerical solution of fourth-order time-fractional partial differential equations with variable coefficients. J. Appl. Anal. Comput. 5(1):52–63

    MathSciNet  Google Scholar 

  • Jin B, Lazarov R, Sheen D, Zhou Z (2016) Error estimates for approximations of distributed order time fractional diffusion with nonsmooth data. Fract. Calc. Appl. Anal. 19(1):69–93

    MathSciNet  Google Scholar 

  • Kamran G, Ali JF (2020) Gómez-Aguilar, Approximation of partial integro-differential equations with a weakly singular kernel using local meshless method. Alex. Eng. J. 59(4):2091–2100

    Google Scholar 

  • Le Gia QT, McLean W (2014) Solving the heat equation on the unit sphere via Laplace transforms and radial basis functions. Adv. Comput. Math. 40(2):353–375

    MathSciNet  Google Scholar 

  • López-Fernández M, Palencia C (2004) On the numerical inversion of the Laplace transform of certain holomorphic mappings. Appl. Numer. Math. 51(2–3):289–303

    MathSciNet  Google Scholar 

  • McLean W, Sloan IH, Thomée V (2006) Time discretization via Laplace transformation of an integro-differential equation of parabolic type. Numer. Math. 102(3):497–522

    MathSciNet  Google Scholar 

  • McLean W, Thomée V (2004) Time discretization of an evolution equation via Laplace transforms. IMA J. Numer. Anal. 24(3):439–463

    MathSciNet  Google Scholar 

  • McLean W, Thomée V (2010) Maximum-norm error analysis of a numerical solution via Laplace transformation and quadrature of a fractional-order evolution equation. IMA J. Numer. Anal. 30(1):208–230

    MathSciNet  Google Scholar 

  • McLean W, Thomée V (2010) Numerical solution via Laplace transforms of a fractional order evolution equation. J. Integral Equ. Appl. 22(1):57–94

    MathSciNet  Google Scholar 

  • Miller KS, Ross B (1993) An introduction to the fractional calculus and fractional differential equations, Wiley

  • Mohammadi-Firouzjaei H, Adibi M, Adibi H (2022) Local discontinuous Galerkin method for the numerical solution of fractional compartmental model with application in pharmacokinetics. J. Math. Model. 10(2):247–261

    MathSciNet  Google Scholar 

  • Mohammadi-Firouzjaei H, Adibi H, Dehghan M (2021) Local discontinuous Galerkin method for distributed-order time-fractional diffusion-wave equation: Application of Laplace transform. Math. Methods Appl. Sci. 44(6):4923–4937

    MathSciNet  Google Scholar 

  • Mohammadi-Firouzjaei H, Adibi H, Dehghan M (2022) A comparative study on interior penalty discontinuous Galerkin and enriched Galerkin methods for time-fractional Sobolev equation. Eng. Comput. 38:5379–5394

    Google Scholar 

  • Mohammadi-Firouzjaei H, Adibi H, Dehghan M (2023) Study of the backward difference and local discontinuous Galerkin (LDG) methods for solving fourth-order partial integro-differential equations (PIDEs) with memory terms: Stability analysis. Appl. Numer. Math. 184:567–580

    MathSciNet  Google Scholar 

  • Monk P (1987) A mixed finite element method for the biharmonic equation. SIAM J. Numer. Anal. 24(4):737–749

    MathSciNet  Google Scholar 

  • Podlubny I (1998) Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications, Elsevier, Vol. 198

  • Qiu L, Deng W, Hesthaven JS (2015) Nodal discontinuous Galerkin methods for fractional diffusion equations on 2D domain with triangular meshes. J. Comput. Phys. 298:678–694

    MathSciNet  Google Scholar 

  • Qiu W, Xu D, Guo J (2021) The Crank-Nicolson-type Sinc-Galerkin method for the fourth-order partial integro-differential equation with a weakly singular kernel. Appl. Numer. Math. 159:239–258

    MathSciNet  Google Scholar 

  • Renardy M (1989) Mathematical analysis of viscoelastic flows. Ann. Rev. Fluid Mech. 21:21–36

    MathSciNet  Google Scholar 

  • Renardy M, Hrusa WJ, Nohel JA (1987) Mathematical Problem in Viscoelasticity. Longman, London

    Google Scholar 

  • Saadatmandi A, Dehghan M (2010) A new operational matrix for solving fractional-order differential equations. Comput. Math. Appl. 59(3):1326–1336

    MathSciNet  Google Scholar 

  • Saadatmandi A, Dehghan M (2011) A Legendre collocation method for fractional integro-differential equations. J. Vib. Control. 17(13):2050–2058

    MathSciNet  Google Scholar 

  • Sheng H, Li Y, Chen Y (2011) Application of numerical inverse Laplace transform algorithms in fractional calculus. J. Franklin Inst. 348(2):315–330

    MathSciNet  Google Scholar 

  • Talbot A (1979) The accurate numerical inversion of Laplace transforms. IMA. J. Appl. Math. 23(1):97–120

    MathSciNet  Google Scholar 

  • Uddin M, Kamran AA, (2018) A localized transform-based meshless method for solving time fractional wave-diffusion equation. Eng. Anal. Bound. Elem. 92:108–113

  • Uddin M, Kamran K, Usman M, Ali A (2018) On the Laplace-transformed-based local meshless method for fractional-order diffusion equation. Int. J. Comput. Methods Eng. Sci. Mech. 19(3):221–225

    MathSciNet  Google Scholar 

  • Wei L, He Y (2014) Analysis of a fully discrete local discontinuous Galerkin method for time-fractional fourth-order problems. Appl. Math. Model. 38(4):1511–1522

    MathSciNet  Google Scholar 

  • Weideman J, Trefethen L (2007) Parabolic and hyperbolic contours for computing the Bromwich integral. Math. Comput. 76(259):1341–1356

    MathSciNet  Google Scholar 

  • Xu D, Qiu W, Guo J (2020) A compact finite difference scheme for the fourth-order time-fractional integro-differential equation with a weakly singular kernel. Numer. Methods Partial Differ. Equ. 36(2):439–458

    MathSciNet  Google Scholar 

  • Xu X, Xu D (2018) A semi-discrete scheme for solving fourth-order partial integro-differential equation with a weakly singular kernel using Legendre wavelets method. Comput. Appl. Math. 37(4):4145–4168

    MathSciNet  Google Scholar 

  • Yang X, Xu D, Zhang H (2011) Quasi-wavelet based numerical method for fourth-order partial integro-differential equations with a weakly singular kernel. Int. J. Comput. 88(15):3236–3254

    MathSciNet  Google Scholar 

  • Yang X, Xu D, Zhang H (2013) Crank-Nicolson/quasi-wavelets method for solving fourth-order partial integro-differential equation with a weakly singular kernel. J. Comput. Phys. 234:317–329

    MathSciNet  Google Scholar 

  • Zhang H, Han X, Yang X (2013) Quintic B-spline collocation method for fourth-order partial integro-differential equations with a weakly singular kernel. Appl. Math. Comput. 219(12):6565–6575

    MathSciNet  Google Scholar 

Download references

Acknowledgements

We want to express our gratitude to the reviewers for their valuable suggestions and comments that helped to enhance the paper

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Faculty of Mathematics and Computer Sciences, Amirkabir University of Technology (Tehran Polytechnique), No. 424, Hafez Ave., Tehran, 15914, Iran

    Hadi Mohammadi-Firouzjaei, Hojatollah Adibi & Mehdi Dehghan

Authors
  1. Hadi Mohammadi-Firouzjaei
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hojatollah Adibi
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Mehdi Dehghan
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors made equal contribution.

Corresponding author

Correspondence to Mehdi Dehghan.

Ethics declarations

Conflict of interest

There is no potential conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mohammadi-Firouzjaei, H., Adibi, H. & Dehghan, M. Computational study based on the Laplace transform and local discontinuous Galerkin methods for solving fourth-order time-fractional partial integro-differential equations with weakly singular kernels. Comp. Appl. Math. 43, 324 (2024). https://doi.org/10.1007/s40314-024-02813-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-024-02813-4

Keywords

Mathematics Subject Classification