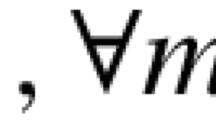Abstract
Note that \(\Theta \)–\(\Xi \) functions and aggregation functions are two interrelated concepts rather than mutually inclusive ones. On the other hand, 0-overlap functions and 1-grouping functions are common subsets of these two broader categories. Although the homogeneity and quasi-homogeneity properties of 0-overlap functions and 1-grouping functions have been thoroughly described through existing research on aggregation functions, it is noteworthy that our approach offers a direct proof of their homogeneity, rather than treating them as a mere special case of quasi-homogeneity. Then the pseudo-homogeneity of these functions is extended to aggregation functions with continuous diagonals, and the necessary and sufficient conditions for such aggregation functions are obtained by utilizing the pseudo-inverses of unary functions. Finally, by exploring the structures of the \(\Theta \)–\(\Xi \) functions, which serve as a unified representation of 0-overlap functions and 1-grouping functions, the homogeneity, quasi-homogeneity, and pseudo-homogeneity of \(\Theta \)–\(\Xi \) functions are comprehensively characterized. Our findings are further illustrated through examples, providing a clear understanding of these functions and their properties.




Similar content being viewed by others
Data availability
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
References
Alsina C, Schweizer B, Frank MJ (2006) Associative functions: triangular norms and copulas. World Scientific Press, Singapore
Bedregal B, Dimuro GP, Bustince H, Barrenechea E (2013) New results on overlap and grouping functions. Inf Sci 249:148–170
Beliakov G, Pradera A, Calvo T (2007) Aggregation functions: a guide for practitioners. Studies in fuzziness and soft computing, 221, Springer Berlin, Heidelberg
Bustince H, Fernandez J, Mesiar R (2009) Overlap index, overlap functions and migrativity. In: Proceedings of the joint 2009 international fuzzy systems association world congress and 2009 European society of fuzzy logic and technology conference, Lisbon, Portugal, 20–24 July
Bustince H, Pagola M, Mesiar R et al (2012) Grouping, overlaps, and generalized bientropic functions for fuzzy modeling of pairwise comparisons. IEEE Trans Fuzzy Syst 20:405–415
Cabrera G, Matthias E, Andrew M et al (2014) Multi-objective optimisation of positively homogeneous functions and an application in radiation therapy. Oper Res Lett 42:268–272
Cheng HD, Chen CH, Chi HH (1997) Image segmentation using fuzzy homogeneity criterion. Inf Sci 98:237–262
Dimuro GP, Bedregal B et al (2016) On additive generators of overlap functions. Fuzzy Sets Syst 287:76–96
Dimuro GP, Asmus TD, Pinheiro J et al (2022) On construction methods of (interval-valued) general grouping functions. In: International conference on information processing and management of uncertainty, pp 359–371
Ebanks BR (1998) Quasi-homogeneous associative functions. Int J Math Math Sci 21:351–357
Elkano M, Galar M, Sanz JA et al (2018) Consensus via penalty functions for decision making in ensembles in fuzzy rule-based classification systems. Appl Soft Comput 67:728–740
Fuss M, McFadden D, Mundlak Y (1978) A survey of functional forms in the economic analysis of production. Histoy of economic thought Chapters 1
Garcia-Jimenez S, Bustince H, Hullermeier E et al (2015) Overlap indices: construction of and application to interpolative fuzzy systems. IEEE Trans Fuzzy Syst 23:1259–1273
Gómez D, Rodríguez JT, Montero J et al (2015) Fuzzy community detection based on grouping and overlapping functions. In: Conference of international fuzzy systems association and European society for fuzzy logic and technology, pp 1514–1519
Gómez D, Rodríguez JT, Montero J et al (2016) n-Dimensional overlap functions. Fuzzy Sets Syst 287:57–75
Jurio A, Bustince H, Pagola M et al (2013) Some properties of overlap and grouping functions and their application to image thresholding. Fuzzy Sets Syst 229:69–90
Kannappan P (2009) Functional equations and inequalities with applications. Springer, New York
Klement EP, Mesiar R, Pap E (2000) Triangular norms. Kluwer, Dordrecht
Lima L, Bedregal B, Rocha M et al (2020) On some classes of nullnorms and h-pseudo homogeneity. Fuzzy Sets Syst 427:23–36
Mayor G, Mesiar R, Torrens J (2008) On quasi-homogeneous copulas. Kybernetika 44:745–756
Mesiarová-Zemánková A (2017) Characterization of uninorms with continuous underlying t-norm and t-conorm by means of the ordinal sum construction. IEEE Trans Fuzzy Syst 83:176–192
Mesiar R, Borkotokey S et al (2018) Aggregation under uncertainty. IEEE Trans Fuzzy Syst 26:2475–2478
Miguel LD, Gómez D, Rodríguez JT et al (2019) General overlap functions. Fuzzy Sets Syst 372:81–96
Nolasco DHS, Costa FB, Palmeira ES et al (2019) Wavelet-fuzzy power quality diagnosis system with inference method based on overlap functions: case study in an AC microgrid. Eng Appl Artif Intell 85:284–294
Pérez-Fernández R, De Baets B (2021) Aggregation theory revisited. IEEE Trans Fuzzy Syst 29:797–804
Qiao JS (2023) A unified framework of 0-overlap functions and 1-grouping functions. Fuzzy Sets Syst 469:108638
Qiao JS, Hu BQ (2017) On interval additive generators of interval overlap functions and interval grouping functions. Fuzzy Sets Syst 323:19–55
Qiao JS, Hu BQ (2019) On homogeneous, quasi-homogeneous and pseudo-homogeneous overlap and grouping functions. Fuzzy Sets Syst 357:58–90
Qiao JS, Zhao B (2022) On \(\alpha \)-cross-migrativity of overlap (0-overlap) functions. IEEE Trans Fuzzy Syst 30:448–461
Rückschlossová T, Rückschloss R (2006) Homogeneous aggregation operators. Kybernetika 42:279–286
Saha PK, Udupa JK (2001) Optimum image thresholding via class uncertainty and region homogeneity. IEEE Trans Pattern Anal Mach Intell 23:689–706
Santiago RH, Bedregal BR, Dimuro GP et al (2022) Abstract homogeneous functions and consistently influenced/disturbed multi-expert decision making. IEEE Trans Fuzzy Syst 30:3447–3459
Santos HS, Dimuro GP, Asmus TD et al (2020) General grouping functions. Inf Process Manag Uncertainty Knowl-Based Syst 1238:481–495
Su Y, Zong W, Mesiar R (2022) Characterization of homogeneous and quasi-homogeneous binary aggregation functions. Fuzzy Sets Syst 433:96–107
Wang XP, Zhu FQ (2023) Note on the pseudo-homogeneous overlap and grouping functions. Fuzzy Sets Syst 473:108715
Xie AF, Su Y, Liu H (2016) On pseudo-homogeneous triangular norms, triangular conorms and proper uninorms. Fuzzy Sets Syst 287:203–212
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos. 12371459, 12331016), the Jiangxi Provincial Natural Science Foundation (Nos. 20232ACB201002, 20224BCD41001), and the Guangdong Philosophy and Social Science Planning Project (No. GD23XSH03).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Liu, C., Qin, F., Qiao, J. et al. (Quasi, pseudo)-homogeneity of \(\Theta \)–\(\Xi \) functions. Comp. Appl. Math. 44, 11 (2025). https://doi.org/10.1007/s40314-024-02971-5
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40314-024-02971-5