Skip to main content
Springer Nature Link
Log in

Random periodic paths of stochastic periodic semi-flows through random attractors, synchronizations and Lyapunov exponents

  • Published:
Computational and Applied Mathematics Aims and scope Submit manuscript

Abstract

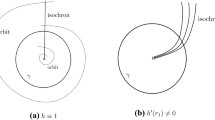
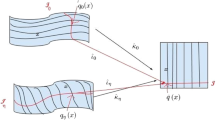
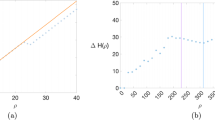
This paper discusses the existence and uniqueness of random periodic paths of stochastic periodic semi-flows. Random periodic attractors are introduced and synchronization for stochastic periodic semi-flows is proved under some conditions to find the unique random periodic path. The multiplicative ergodic theorem of stochastic periodic semi-flows is proved to characterize Lyapunov exponents. The Benzi–Parisi–Sutera–Vulpiani climate model is an example to verify the results by estimating the negative Lyapunov exponent constructed by the density function from the Fokker–Planck equation. Numerical approximations are performed with great agreement. A case of gradient systems is considered to be another example of a negative Lyapunov exponent.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data availability

Not applicable.

References

  • Arnold L (2003) Random dynamical systems. Springer, Berlin

    Google Scholar 

  • Arnold VI, Kozlov VV, Neishtadt AI (2006) Mathematical aspects of classical and celestial mechanics, 3rd edn. Springer, New York

    Book  Google Scholar 

  • Bates PW, Lu K, Wang B (2014) Attractors of non-autonomous stochastic lattice systems in weighted spaces. Physica D 289:32–50

    Article  MathSciNet  Google Scholar 

  • Benzi R, Parisi G, Sutera A, Vulpiani A (1982) Stochastic resonance in climatic change. Tellus 34:10–16

    Article  Google Scholar 

  • Cherubini AM, Lamb J, Rasmussen M, Sato Y (2017) A random dynamical systems perspective on stochastic resonance. Nonlinearity 30:2835–2853

    Article  MathSciNet  Google Scholar 

  • Crauel H, Flandoli F (1994) Attractor for random dynamical systems. Probab Theory Relat Fields 100:365–393

    Article  MathSciNet  Google Scholar 

  • Crauel H, Debussche A, Flandoli F (1997) Random attractor. J Dyn Differ Equ 9:307–341

    Article  MathSciNet  Google Scholar 

  • Da Prato G, Sinestrari E (1987) Differential operators with non dense domain. Annali della Scuola Normale Superiore di Pisa - Classe di Scienze, Serie 4(14):285–344

    Google Scholar 

  • Feng C, Zhao H (2012) Random periodic solutions of SPDEs via integral equations and Wiener–Sobolev compact embedding. J Funct Anal 262:4377–4422

    Article  MathSciNet  Google Scholar 

  • Feng C, Zhao H (2020) Random periodic processes, periodic measures and ergodicity. J Differ Equ 269:7382–7428

    Article  MathSciNet  Google Scholar 

  • Feng C, Zhao H, Zhou B (2011) Pathwise random periodic solutions of stochastic differential equations. J Differ Equ 251:119–149

    Article  MathSciNet  Google Scholar 

  • Feng C, Liu Y, Zhao H (2017) Numerical approximation of random periodic solutions of stochastic differential equations. Z Angew Math Phys 68:119

    Article  MathSciNet  Google Scholar 

  • Feng C, Liu Y, Zhao H (2023a) Periodic measures and Wasserstein distance for analyzing periodicity of time series datasets. Commun Nonlinear Sci Numer Simul 120:107166

    Article  Google Scholar 

  • Feng C, Zhao H, Zhong J (2023b) Existence of geometric ergodic periodic measures of stochastic differential equations. J Differ Equ 359:67–106

    Article  MathSciNet  Google Scholar 

  • Flandoli F, Gess B, Scheutzow M (2017) Synchronization by noise. Probab Theory Relat Fields 168:511–556

    Article  MathSciNet  Google Scholar 

  • Le Jan Y (1987) équilibre statistique pour les produits de difféomorphismes aléatoires indépendants. Annales de l’I.H.P. Probabilités et statistiques 23:111–120

    Google Scholar 

  • Newman J (2018) Necessary and sufficient conditions for stable synchronization in random dynamical systems. Ergod Theory Dyn Syst 38:1857–1875

    Article  MathSciNet  Google Scholar 

  • Oseledets VI (1968) A multiplicative ergodic theorem, Lyapunov characteristic numbers for dynamical systems. Trans Mosc Math Soc 19:197–231

    Google Scholar 

  • Poincare H (1881) Mémoire sur les courbes définies par une Équation différentielle. J Math Pures Appl 3:375–442. Additional parts published in 3: 251–296 (1882); 4:167–244 (1885); 4:151–217 (1886)

  • Schmalfuß B (1992) Backward cocycle and attractors of stochastic differential equations. In: International seminar on applied mathematics-nonlinear dynamics: attractor approximation and global behavior

  • Wang B (2012) Sufficient and necessary criteria for existence of pullback attractors for non-compact random dynamical systems. J Differ Equ 253:1544–1583

    Article  MathSciNet  Google Scholar 

  • Zhao H, Zheng ZH (2009) Random periodic solutions of random dynamical systems. J Differ Equ 246:2020–2038

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Yan Luo thanks the National Natural Science Foundation of China (NSFC) for the support of this research (Grant: 12471142).

Author information

Authors and Affiliations

  1. Department of Mathematical Sciences, Durham University, Durham, DH1 3LE, UK

    Chunrong Feng

  2. Research Centre for Mathematics and Interdisciplinary Sciences, Shandong University, Qingdao, 266237, China

    Chunrong Feng & Yan Luo

Authors
  1. Chunrong Feng
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yan Luo
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yan Luo.

Ethics declarations

Conflict of interest

The authors declare that there are no Conflict of interest, we do not have any possible Conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Feng, C., Luo, Y. Random periodic paths of stochastic periodic semi-flows through random attractors, synchronizations and Lyapunov exponents. Comp. Appl. Math. 44, 179 (2025). https://doi.org/10.1007/s40314-025-03135-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s40314-025-03135-9

Keywords

Mathematics Subject Classification