Skip to main content

Advertisement

Springer Nature Link
Log in

Adaptive Fuzzy Terminal Sliding-Mode Observer with Experimental Applications

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

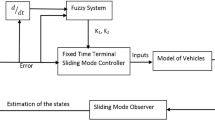
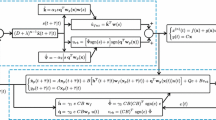
Abstract

In this paper, conventional gradient-descent-based adaptive fuzzy observer is improved by using the terminal sliding-mode theory for a class of nonlinear systems. The improvement is made in two ways: first, the switching term of the sliding-mode approach is added to the state of the observer. Second, the measurement error of the system is designed as the input of the observer instead of measured state. The stability of the observer and boundedness of the parameters are proved using Lyapunov approach. Contributions of the paper are summarized as follows: (i) the robustness and convergence properties of newly proposed observer are improved, (ii) the proposed adaptive fuzzy terminal sliding-mode observer, conventional adaptive fuzzy observer, adaptive neural-network observer, and Euler filtering approaches are compared in terms of their ability to estimate velocities of three real-time experimental systems reliably. The performance of the designed observers is discussed with root mean squared-error criterion where the proposed adaptive fuzzy terminal sliding-mode observer provided much accurate state estimation results than classical observers.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Luenberger, D.: Observers for multivariable systems. IEEE Trans. Autom. Control 11(2), 190–197 (1966)

    Article  Google Scholar 

  2. Thau, E.E.: Observing the state of nonlinear systems. Int. J. Control 17, 471–479 (1973)

    Article  MATH  Google Scholar 

  3. Birk, J., Zeitz, M.: Extended-Luenberger observer for non-linear multivariable systems. Int. J. Control 47(6), 1823–1836 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  4. Cox, H.: On the estimation of state variables and parameters for noisy dynamic systems. IEEE Trans. Autom. Control 9(1), 5–12 (1964)

    Article  MathSciNet  Google Scholar 

  5. Simon, D.: Optimal State Estimation: Kalman, H-Infinity, and Nonlinear Approaches. Wiley-Interscience, Hoboken (2006)

    Book  Google Scholar 

  6. Drakunov, S.V.: An adaptive quasioptimal filter with discontinuous parameters. Autom. Remote Control 44(9), 1167–1175 (1983)

    MathSciNet  MATH  Google Scholar 

  7. Slotine, J.J.E., Hedrick, J.K., Misawa, E.A.: On sliding observers for nonlinear systems. ASME J. Dyn. Syst. Control 109, 245–252 (1987)

    Article  MATH  Google Scholar 

  8. Gauthier, J.P., Hammouri, H., Othman, S.: A simple observer for nonlinear systems applications to bioreactors. IEEE Trans. Autom. Control 37(6), 875–880 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  9. Tanaka, K., Wang, H.O.: Fuzzy regulators and fuzzy observers: alinear matrix inequality approach. In: Proceedings of the 36thIEEE Conference on Decision and Control, vol. 2, pp. 1315–1320, San Diego, California, 1997

  10. Beyhan, S.: Runge–Kutta model-based nonlinear observer for synchronization and control of chaotic systems. ISA Trans. 52(4), 501–509 (2013)

    Article  Google Scholar 

  11. Iplikci, S.: Runge–Kutta model-based adaptive predictive control mechanism for non-linear processes. Trans. Inst. Meas. Control 35(2), 166–180 (2013)

    Article  Google Scholar 

  12. Al-Hosani, K., Utkin, V.I.: Parameters estimation using sliding mode observer with shift operator. J. Frankl. Inst. 349(4), 1509–1525 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  13. Spurgeon, S.K.: Sliding mode observers: a survey. Int. J. Syst. Sci. 39(8), 751–764 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  14. Ahmed, M.S., Riyaz, S.H.: Dynamic observers—a neural net approach. J. Intell. Fuzzy Syst. 9(1,2), 113–127 (2000)

    Google Scholar 

  15. Kim, Y.H., Lewis, F.L., Abdallah, C.T.: A dynamic recurrent neural-network-based adaptive observer for a class of nonlinear systems. Automatica 33(8), 1539–1543 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  16. Park, JH., Yoon, PS., Park, GT.: Robust adaptive observer using fuzzy systems for uncertain nonlinear systems. In: The 10th IEEE International Conference on Fuzzy Systems, vol. 3, pp. 749–752, The University of Melbourne, Australia, 2001

  17. Boulkroune, A., Tadjine, M., M’Saad, M., Farza, M.: How to design a fuzzy adaptive controller based on observers for uncertain affine nonlinear systems. Fuzzy Sets Syst. 159(8), 926–948 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  18. Leu, Y.-G., Lee, T.-T., Wang, W.-Y.: Observer-based adaptive fuzzy-neural control for unknown nonlinear dynamical systems. IEEE Trans. Syst. Man Cybern. Part B 29(5), 583–591 (1999)

    Article  Google Scholar 

  19. Lian, K.-Y., Hong, C.-W.: Current-sensorless flyback converters using integral T–S fuzzy approach. Int. J. Fuzzy Syst. 15(1), 66–74 (2013)

    MathSciNet  Google Scholar 

  20. Wang, L.-K., Liu, X.-D.: Robust H\(_\infty\) fuzzy output feedback control for uncertain discrete-time nonlinear systems. Int. J. Fuzzy Syst. 12(3), 218–226 (2010)

    MathSciNet  Google Scholar 

  21. Zhang, L., Tong, S., Li, Y.: Adaptive fuzzy output-feedback control with prescribed performance for uncertain nonlinear systems. Int. J. Fuzzy Syst. 16(2), 212–221 (2014)

    Article  MathSciNet  Google Scholar 

  22. Lin, F.-C., Yang, S.-M.: Adaptive fuzzy logic-based velocity observer for servo motor drives. Mechatronics 13(3), 229–241 (2003)

    Article  Google Scholar 

  23. Merry, R.J.E., van de Molengraft, M.J.G., Steinbuch, M.: Velocity and acceleration estimation for optical incremental encoders. Mechatronics 20(1), 20–26 (2010)

    Article  Google Scholar 

  24. Feng, Y., Zheng, J., Xinghuo, Y., Truong, N.-V.: Hybrid terminal sliding-mode observer design method for a permanent-magnet synchronous motor control system. Industrial Electronics, IEEE Transactions on 56(9), 3424–3431 (2009)

    Article  Google Scholar 

  25. Tan, C.P., Yu, X., Man, Z.: Terminal sliding mode observers for a class of nonlinear systems. Automatica 46(8), 1401–1404 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  26. Yuqiang, W., Xinghuo, Y., Man, Z.: Terminal sliding mode control design for uncertain dynamic systems. Syst. Control Lett. 34(5), 281–287 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  27. Wang, L.X.: A Course in Fuzzy Systems and Control. Prentice-Hall Inc., London (1997)

    MATH  Google Scholar 

  28. Beyhan, S.: Adaptive dynamic neural-network observer design of velocity feedbacks. In: Innovations in Intelligent Systems and Applications (INISTA), 2012 International Symposium on, pages 1–5, Trabzon, Turkey, July 2012

  29. Akçay, H., Ninness, B.: Orthonormal basis functions for modelling continuous-time systems. Signal Process. 77(3), 261–274 (1999)

    Article  MATH  Google Scholar 

  30. Xinghuo, Y., Zhihong, M.: Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I 49(2), 261–264 (2002)

    Article  MathSciNet  Google Scholar 

  31. Ionnou, P.A., Sun, J.: Robust Adaptive Control. Prentice-Hall, Englewood Cliffs (1996)

    Google Scholar 

  32. Tan, C.P., Edwards, C.: Sliding mode observers for robust detection and reconstruction of actuator and sensor faults. Int. J. Robust Nonlinear Control 13(5), 443–463 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  33. Kim, Y.-T., Zenn Bien, Z.: Robust adaptive fuzzy control in the presence of external disturbance and approximation error. Fuzzy Sets Syst. 148(3), 377–393 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  34. Quanser Inc. Quanser Inc., Canada, Rotary Flexible Joint User Manual, 2012

  35. Feedback Inc. Digital Pendulum Control Experiments, 33-936s, Feedback Intruments ltd., 2006

  36. Levant, A.: Robust exact differentiation via sliding mode technique. Automatica 34(3), 379–384 (1998)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

The author thanks Delft Center for Systems and Control institute staff to collect experimental data from flexible-link transmission system. This paper is supported by a project of Pamukkale University Scientific Project Council (BAP) under grant number 2013BSP008.

Author information

Authors and Affiliations

  1. Department of Electrical and Electronics Engineering, Pamukkale University, Kinikli Campus, 20070, Denizli, Turkey

    Selami Beyhan

Authors
  1. Selami Beyhan
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Selami Beyhan.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Beyhan, S. Adaptive Fuzzy Terminal Sliding-Mode Observer with Experimental Applications. Int. J. Fuzzy Syst. 18, 585–594 (2016). https://doi.org/10.1007/s40815-015-0102-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-015-0102-8

Keywords