Skip to main content

Advertisement

Springer Nature Link
Log in

A Fuzzy Control Approach to Stabilization of Markovian Jump Systems with General Unknown Transition Probabilities

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

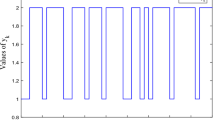
This paper is devoted to the investigation of the stability and stabilization problems for a class of Markovian jump nonlinear systems with general unknown transition rates (GUTRs) via fuzzy control. The Takagi-Sugeno (T-S) fuzzy model is utilized to characterize the Markovian jump nonlinear systems with general unknown transition probabilities. Some sufficient criteria on stochastic stability are derived in terms of linear matrix inequalities, and a mode-dependent fuzzy controller is designed. The derived results extend the conclusions recently presented by Sheng and Gao (Stabilization for Markovian jump nonlinear systems with partly unknown transition probabilities via fuzzy control, Fuzzy Set Syst 161(21): 2780–2792, 2010). In fact, the system discussed in Sheng and Gao (Fuzzy Set Syst 161(21) 2780–2792, 2010) is a special case of ours, because their transition rates are completely known or completely unknown, while in our GUTR T-S fuzzy model, each transition rate can be completely unknown or only its estimate value is known. Finally, a numerical example is present to illustrate the effectiveness and applicability of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Krasovskii, N.N., Lidskii, E.A.: Analysis and design of controllers in systems with random attributes. Autom. Remote Control 22(1), 1021–1025 (1961)

    MathSciNet  Google Scholar 

  2. Mao, X., Yuan, C.: Stochastic Differential Equations with Markovian Switching. Imperial College Press, London (2006)

    Book  MATH  Google Scholar 

  3. Kao, Y.G., Wang, C.H., Zha, F.S., Cao, H.X.: Stability in mean of partial variables for stochastic reaction-diffusion systems with Markovian switching. J. Frankl. Inst. 351(1), 500–512 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  4. Xia, Y.Q., Boukas, E.K., Shi, P., Zhang, J.H.: Stability and stabilization of continuous-time singular hybrid systems. Automatica 45(6), 1504–1509 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  5. Zhao, X., Zhang, L., Shi, P.: Stability of a class of switched positive linear time-delay systems. Int. J. Robust Nonlinear Control 23(5), 578–589 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  6. Kao, Y.G., Guo, J.F., Wang, C.H., Sun, X.Q.: Delay-dependent robust exponential stability of Markovian jumping reaction-diffusion Cohen-Grossberg neural networks with mixed delays. J. Frankl. Inst. 349(6), 1972–1988 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  7. Kao, Y.G., Wang, C.H., Karimi, H.R., Bi, R.: Global stability of coupled Markovian switching reaction-diffusion systems on networks. Nonlinear Anal. 13, 61–73 (2014)

    MathSciNet  MATH  Google Scholar 

  8. Kao, Y.G., Li, W., Wang, C.H.: Non-fragile observer based \(H_{\infty }\) sliding mode control for Ito stochastic systems with Markovian switching. Int. J. Robust Nonlinear Control 24(15), 2035–2047 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  9. Kao, Y.G., Xie, J., Wang, C.H., Karimi, H.R.: A sliding mode approach to \(H_{\infty }\) non-fragile observer-based control design for uncertain Markovian neutral-type stochastic systems. Automatica 52, 218–226 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  10. Liu, M., Shi, P., Zhang, L.X., Zhao, X.: Fault-tolerant control for nonlinear Markovian jump systems via proportional and derivative sliding mode observer technique. IEEE Trans. Circuits Syst. I 58(11), 2755–2764 (2011)

    Article  MathSciNet  Google Scholar 

  11. Wu, L., Su, X., Shi, P.: Sliding mode control with bounded \(H_{2}\) gain performance of Markovian jump singular time-delay systems. Automatica 48(8), 1929–1933 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  12. Wu, Z., Su, H., Chu, J.: \(H_{\infty }\) model reduction for discrete singular Markovian jump systems. Proc. Inst. Mech. Eng. 223(7), 1017–1025 (2009)

    Google Scholar 

  13. Wu, Z., Shi, P., Su, H., Chu, J.: Asynchronous \(L_{2}\)-\(L_{\infty }\) filtering for discrete-time stochastic Markov jump systems with randomly occurred sensor nonlinearities. Automatica 50(1), 180–186 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  14. Zhang, L.X., Cui, N., Liu, M., Zhao, Y.: Asynchronous filtering of discrete-time switched linear systems with average dwell time. IEEE Trans. Circuits Syst. I 58(5), 1109–1118 (2011)

    Article  MathSciNet  Google Scholar 

  15. Karan, M., Shi, P., Kaya, C.: Transition probability bounds for the stochastic stability robustness of continuous- and discrete-time Markovian jump linear systems. Automatica 42(12), 2159–2168 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  16. Shi, P., Boukas, E.K.: \(H_{\infty }\) control for Markovian jumping linear systems with parametric uncertainty. J. Optim. Theory Appl. 95(1), 75–99 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  17. Xiong, J., Lam, J.: Robust \(H_{2}\) control of Markovian jump systems with uncertain switching probabilities. Int. J. Syst. Sci. 40(3), 255–265 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  18. Xiong, J., Lam, J., Gao, H., Ho, D.W.C.: On robust stabilization of Markovian jump systems with uncertain switching probabilities. Automatica 41(5), 897–903 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  19. Zhang, L.X., Boukas, E.K., Lam, J.: Analysis and synthesis of Markov jump linear systems with time-varying delays and partially known transition probabilities. IEEE Trans. Autom. Control 53(10), 2458–2462 (2008)

    Article  MathSciNet  Google Scholar 

  20. Zhang, L.X., Boukas, E.K.: Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities. Automatica 45(2), 436–468 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  21. Zhang, L.X., Boukas, E.K.: Mode-dependent \(H_{\infty }\) filtering for discrete-time Markovian jump linear systems with partly unknown transition probabilities. Automatica 45(6), 1462–1467 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  22. Zhang, L.X., Boukas, E.K.: \(H_{\infty }\) control for discrete-time Markovian jump linear systems with partly unknown transition probabilities. Int. J. Robust Nonlinear Control 19(8), 868–883 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  23. Zhang, Y., He, Y., Wu, M., Zhang, J.: Stabilization for Markovian jump systems with partial information on transition probability based on free-connection weighting matrices. Automatica 47(1), 79–84 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  24. Sheng, L., Gao, M.: Stabilization for Markovian jump nonlinear systems with partly unknown transition probabilities via fuzzy control. Fuzzy Sets Syst. 161(21), 2780–2792 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  25. Shen, M., Ye, D.: Improved fuzzy control design for nonlinear Markovian jump systems with incomplete transition descriptions. Fuzzy Sets Syst. 217(3), 80–95 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wei, Y.L., Qiu, J.B., Karimi, H.R., Wang, M.: A new design of \(H_{\infty }\) filtering for continuous-time Markovian jump systems with time-varying delay and partially accessible mode information. Signal Process. 93(9), 2392–2407 (2013)

    Article  Google Scholar 

  27. Wei, Y.L., Wang, M., Qiu, J.B.: New approach to delay-dependent \(H_{\infty }\) filtering for discrete-time Markovian jump systems with time-varying delay and incomplete transition descriptions. IET Control Theory Appl. 7(5), 684–696 (2013)

    Article  MathSciNet  Google Scholar 

  28. Wei, Y.L., Qiu, J.B., Karimi, H.R., Wang, M.: Model reduction for continuous-time Markovian jump systems with incomplete statistics of mode information. Int. J. Syst. Sci. 45(7), 1496–1507 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  29. Guo, Y., Wang, Z.: Stability of Markovian jump systems with generally uncertain transition rates. J. Frankl. Inst. 350(9), 2826–2836 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  30. Kao, Y.G., Shi, L., Xie, J., Karimi, H.R.: Global exponential stability of delayed Markovian jump fuzzy cellular neural networks with generally incomplete transition probability. Neural Netw. 63, 18–30 (2015)

    Article  MATH  Google Scholar 

  31. Kao, Y.G., Xie, J., Wang, C.H.: Stabilisation of singular Markovian jump systems with generally uncertain transition rates. IEEE Trans. Autom. Contr 59(9), 2604–2610 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  32. Kao, Y.G., Xie, J., Zhang, L.X., Karimi, H.R.: A sliding mode approach to robust stabilisation of Markovian jump linear time-delay systems with generally incomplete transition rates. Nonlinear Anal. 17, 70–80 (2015)

    MathSciNet  MATH  Google Scholar 

  33. Qiu, J.B., Feng, G., Gao, H.J.: Fuzzy-model-based piecewise \(H_{\infty }\) static-output-feedback controller design for networked nonlinear systems. IEEE Trans. Fuzzy Syst. 18(5), 919–934 (2010)

    Article  Google Scholar 

  34. Qiu, J., Feng, G., Gao, H.: Observer-based piecewise affine output feedback controller synthesis of continuous-time T-S fuzzy affine dynamic systems using quantized measurements. IEEE Trans. Fuzzy Syst. 20(6), 1046–1062 (2012)

    Article  Google Scholar 

  35. Qiu, J., Feng, G., Gao, H.: Static-output-feedback control of continuous-time TS fuzzy affine systems via piecewise Lyapunov functions. IEEE Trans. Fuzzy Syst. 21(2), 245–261 (2013)

    Article  Google Scholar 

  36. Wu, H., Cai, K.: Mode-independent robust stabilization for uncertain Markovian jump nonlinear systems via fuzzy control. IEEE Trans. Syst. Man Cybern. B 36(3), 509–519 (2006)

    MathSciNet  Google Scholar 

  37. Arrifano, N., Oliveira, V.: Robust \(H_{\infty }\) fuzzy control approach for a class of Markovian jump nonlinear systems. IEEE Trans. Fuzzy Syst. 14(6), 738–754 (2006)

    Article  Google Scholar 

  38. Nguang, S., Assawinchaichote, W., Shi, P.: Robust \(H_{\infty }\) control design for fuzzy singularly perturbed systems with Markovian jumps: an LMI approach. IET Control Theory Appl. 1(1), 893–908 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  39. Wu, H., Cai, K.: Robust fuzzy control for uncertain discrete-time nonlinear Markovian jump systems without mode observations. Inf. Sci. 177(6), 1509–1522 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  40. Dong, J., Yang, G.: Fuzzy controller design for Markovian jump nonlinear systems. Int. J. Control Autom. Syst. 5(6), 712–717 (2007)

    Google Scholar 

  41. Zhang, Y., Xu, S., Zhang, B.Y.: Robust output feedback stabilization for uncertain discrete-time fuzzy Markovian jump systems with time-varying delays. IEEE Trans. Fuzzy Syst. 17(2), 411–420 (2009)

    Article  Google Scholar 

  42. Zhang, Y., Xu, S., Zou, Y., Lu, J.: Delay-dependent robust stabilization for uncertain discrete-time fuzzy Markovian jump systems with mode-dependent time delays. Fuzzy Sets Syst. 164(1), 66–81 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  43. He, S.P., Liu, F.: Filtering-based robust fault detection of fuzzy jumps systems. Fuzzy Sets Syst. 185(1), 95–110 (2011)

    Article  MATH  Google Scholar 

  44. Palm, R., Driankov, D.: Fuzzy switched hybrid systems-modeling and identification. In: Proceedings of the IEEEISIC/CIRA/ISAS Joint Conference, Gaithersburg, MD, pp. 130–135 (1998)

  45. Tanaka, K., Kosaki, T.: Design of a stable fuzzy controller for an articulated vehicle. IEEE Trans. Syst. Man Cybernetics-Part B 27(3), 552–558 (1997)

    Article  Google Scholar 

  46. Zhao, X., Zhang, L., Shi, P., Karimi, H.R.: Novel stability criteria for T-S fuzzy systems. IEEE Trans. Fuzzy Syst. 22(2), 313–323 (2014)

    Article  Google Scholar 

  47. Zhao, X., Yin, Y.: Control of switched nonlinear systems via T-S fuzzy modeling. IEEE Trans. Fuzzy Syst. doi:10.1109/TFUZZ.2015.2450834 (2015)

Download references

Acknowledgments

This research is supported by the National Natural Science Foundations of China (61473097) and National 863 Plan Project (2008 AA04Z401, 2009 AA043404).

Author information

Authors and Affiliations

  1. Software Institute, Dalian Jiaotong University, Dalian, 116028, People’s Republic of China

    Lei Shi

  2. Department of Mathematics, Harbin Institute of Technology (Weihai), Weihai, 264209, People’s Republic of China

    Yonggui Kao

Authors
  1. Lei Shi
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yonggui Kao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yonggui Kao.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shi, L., Kao, Y. A Fuzzy Control Approach to Stabilization of Markovian Jump Systems with General Unknown Transition Probabilities. Int. J. Fuzzy Syst. 18, 1–11 (2016). https://doi.org/10.1007/s40815-015-0114-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-015-0114-4

Keywords