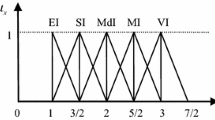
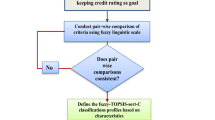
Abstract
In the recent years, various statistical and computational intelligence or machine learning techniques have contributed to the progress of automation or semiautomation for measuring consumer credit scoring in the banking sector. However, most of the Taiwanese commercial banks still rely on seasoned staffs’ judgments on making the final approvals or rejections. To enhance the understanding and transparency of a decision support system (or model) that can assist bank staffs on making their consumer credit loan decisions—while uncertainty exist—is of high business value. One of the promising approaches is multiple rule-based decision-making (MRDM), a subfield of the hybrid multiple criteria decision-making that leverages the advantages of machine learning, soft computing, and decision methods (or techniques). The MRDM approach reveals comprehensible logics (rules or patterns) that can be justified and compared with the existing knowledge of veterans to reinforce the confidence of their judgments. Therefore, in the present study, we propose and compare two MRDM approaches in assisting decision makers on the consumer credit loan evaluations. A set of historical data from a commercial bank in Taiwan is analyzed for illustrating the plausible pros and cons of the two approaches with discussions.



Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.References
Lessmann, S., Baesens, B., Seow, H.V., Thomas, L.C.: Benchmarking state-of-the-art classification algorithms for credit scoring: an update of re-search. Eur. J. Oper. Res. 247(1), 124–136 (2015)
Hand, D.J., Henley, W.E.: Statistical classification methods in consumer credit scoring: a review. J. R. Stat. Soc. Ser A (Stat. Soc.) 160(3), 523–541 (1997)
Sohn, S.Y., Kim, D.H., Yoon, J.H.: Technology credit scoring model with fuzzy logistic regression. Appl. Soft Comput. 43, 150–158 (2016)
Baesens, B., Van Gestel, T., Viaene, S., Stepanova, M., Suykens, J., Vanthienen, J.: Benchmarking state-of-the-art classification algorithms for credit scoring. J. Oper. Res. Soc. 54(6), 627–635 (2003)
Saaty, T.L.: How to make a decision: the analytic hierarchy process. Eur. J. Oper. Res. 48(1), 9–26 (1990)
Saaty, T.L.: Decision making—the analytic hierarchy and network processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 13(1), 1–35 (2004)
Wu, W., Kou, G., Peng, Y.: Group decision-making using improved mul-ti-criteria decision making methods for credit risk analysis. Filomat 30(15), 4135–4150 (2016)
Ignatius, J., Hatami-Marbini, A., Rahman, A., Dhamotharan, L., Khoshnevis, P.: A fuzzy decision support system for credit scoring. Neural Comput. Appl. 29(10), 921–937 (2018)
Zhu, X., Li, J., Wu, D., Wang, H., Liang, C.: Balancing accuracy, complexity and interpretability in consumer credit decision making: a C-TOPSIS classification approach. Knowl.-Based Syst. 52, 258–267 (2013)
Shen, K.Y., Tzeng, G.H.: DRSA-based neuro-fuzzy inference systems for the financial performance prediction of commercial banks. Int. J. Fuzzy Syst. 16(2), 173–183 (2014)
Shen, K.Y., Tzeng, G.H.: A decision rule-based soft computing model for supporting financial performance improvement of the banking industry. Soft. Comput. 19(4), 859–874 (2015)
Marqués, A.I., García, V., Sánchez, J.S.: On the suitability of resampling techniques for the class imbalance problem in credit scoring. J. Oper. Res. Soc. 64(7), 1060–1070 (2013)
Louzada, F., Ara, A., Fernandes, G.B.: Classification methods applied to credit scoring: systematic review and overall comparison. Surv. Oper. Res. Manag. Sci. 21(2), 117–134 (2016)
Thomas, L.C., Edelman, D.B., Crook, J.N.: Credit Scoring and its Applications. Society for Industrial and Applied Mathematics, Philadelphia (2002)
Blöchlinger, A., Leippold, M.: Economic benefit of powerful credit scoring. J. Bank. Finance 30(3), 851–873 (2006)
Tzeng, G.H., Shen, K.Y.: New Concepts and Trends of Hybrid Multiple Criteria Decision Making. CRC Press, Taylor & Francis Group (2017). ISBN 978-1-4987-7708-7
Pawlak, Z.: Rough sets. Int. J. Parallel Prog. 11(5), 341–356 (1982)
Pawlak, Z.: Rough set theory and its applications to data analysis. Cybern. Syst. 29(7), 661–688 (1998)
Zadeh, L.A.: The role of fuzzy logic in the management of uncertainty in expert systems. Fuzzy Sets Syst. 11(1–3), 199–227 (1983)
Tzeng, G.H., Huang, J.J.: Multiple Attribute Decision Making: Methods and Applications. CRC Press, Taylor & Francis Group, New York (2011). ISBN 978-1-4398-6157-8
Zimmermann, H.J.: Fuzzy Sets, Decision Making, and Expert Systems, vol. 10. Springer, Dordrecht (1987)
Sakai, H., Okuma, H., Nakata, M., Ślȩzak, D.: Stable rule extraction and decision making in rough non-deterministic information analysis. Int. J. Hybrid Intell. Syst 8(1), 41–57 (2011)
Durand, D.: Risk Elements in Consumer Instalment Financing. National Bureau of Economic Research, New York (1941)
Greco, S., Matarazzo, B., Słowiński, R.: Rough set approach to multi-attribute choice and ranking problems. In: Making, Multiple Criteria Decision (ed.) Fandel G, Gal T, pp. 318–329. Springer, Berlin (1997)
Greco, S., Matarazzo, B., Słowiński, R.: Rough approximation of a preference relation by dominance relations. Eur. J. Oper. Res. 117(1), 63–83 (1999)
Greco, S., Matarazzo, B., Słowiński, R.: Rough sets theory for multicriteria decision analysis. Eur. J. Oper. Res. 129(1), 1–47 (2001)
Greco, S., Matarazzo, B., Słowiński, R.: Rough sets methodology for sorting problems in presence of multiple attributes and criteria. Eur. J. Oper. Res. 138(2), 247–259 (2002)
Greco, S., Matarazzo, B., Słowiński, R.: Decision rule approach. In: Greco, S., Ehrgott, M., Figueria, J. (eds.) Multiple Criteria Decision Analysis-State of the Art Surveys, pp. 497–552. Springer, New York (2016)
Błaszczyński, J., Słowiński, R., Szeląg, M.: Sequential covering rule induction algorithm for variable consistency rough set approaches. Inf. Sci. 181(5), 987–1002 (2011)
Shen, K.Y., Tzeng, G.H.: A new approach and insightful financial diagnoses for the IT industry based on a hybrid MADM model. Knowl.-Based Syst. 85, 112–130 (2015)
Liou, J.J., Tzeng, G.H.: A dominance-based rough set approach to customer behavior in the airline market. Inf. Sci. 180(11), 2230–2238 (2010)
Greco, S., Ehrgott, M., Figueria, J. (eds.): Multiple Criteria Decision Analysis-State of the Art Surveys, 2nd edn. Springer, New York (2016)
Shen, K.Y., Yan, M.R., Tzeng, G.H.: Combining VIKOR-DANP model for glamor stock selection and stock performance improvement. Knowl.-Based Syst. 58, 86–97 (2014)
Opricovic, S., Tzeng, G.H.: Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 156(2), 445–455 (2004)
Shen, K.Y., Tzeng, G.H.: A novel bipolar MCDM model using rough sets and three-way decisions for decision aids. In: 2016 Joint 8th International Conference on Soft Computing and Intelligent Systems (SCIS) and 17th International Symposium on Advanced Intelligent Systems, pp. 53–58. IEEE (2016a)
Shen, K.Y., Tzeng, G.H.: Contextual improvement planning by fuzzy-rough machine learning: a novel bipolar approach for business analytics. Int. J. Fuzzy Syst. 18(6), 940–955 (2016)
Hwang, C.L., Yoon, K.: Multiple attribute decision making: Methods and application. Lecture Notes in Economics and Mathematical Systems, vol. 186. Springer, New York (1981)
Chen, S.J., Hwang, C.L.: Fuzzy multiple attribute decision making methods. In: Fuzzy Multiple Attribute Decision Making, pp. 289–486. Springer, Berlin(1992)
Nakata, M., Sakai, H.: Lower and upper approximations in data tables containing possibilistic information. In: Transactions on Rough Sets VII, pp. 170–189. Springer, Berlin (2007)
Sakai, H., Wu, M., Nakata, M.: Apriori-based rule generation in incomplete information databases and non-deterministic information systems. Fundam Inform 130(3), 343–376 (2014)
Sakai, H.: (2016). Software tools for RNIA (Rough Non-Deterministic Information Analysis). http://www.mns.kyutech.ac.jp/~sakai/RNIA/
Official website: https://www.dtreg.com/
Shen, K.Y., Zavadska, E.K., Tzeng, G.H.: Updated discussions on “Hybrid multiple criteria decision making methods: A review of applications for sustainability issues”. Economic Research-Ekonomska Istraživanja, accepted (in press) (2018)
Simon, H.A.: Bounded rationality in social science: today and tomorrow. Mind Soc. 1(1), 25–39 (2000)
Atanassov, K.T.: Intuitionistic fuzzy sets. In: Intuitionistic Fuzzy Sets, pp. 1-137. Physica-Verlag HD (1999)
Liu, P.: Special issue “Intuitionistic fuzzy theory and its application in economy, technology and management”. Technol. Econ. Dev. Econ. 22(3), 327–335 (2016). https://doi.org/10.3846/20294913.2016.1185047
Acknowledgements
A pilot study was conducted and reported at the IJCRS2017 conference in Poland (July/2017). The data and opinions from the senior staffs are appreciated. This study received financial supports from two grants under the two project numbers: (1) 104-2410-H-305-052-MY3 and (2) 105-2410-H-034-019-MY2, both from the Ministry of Science and Technology (MOST) of Taiwan.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix: 1
The required steps to form DANP weights are found in [10, 16], which begins from obtained an initial average influence matrix A (in Table 15), and the required steps are as follows:
Step 1 Normalize A into a direct-influence matrix D
Step 2 Get total influence matrix T by \( \varvec{T} = \varvec{D} \times \left( {\varvec{I} - \varvec{D}} \right)^{ - 1} \)
Step 3 Transform T into the unweighted supermatrix W
Step 4 Normalized dimensional matrix \( \varvec{T}_{D}^{N} \)(Table 16)
Step 5 Adjust W by using \( \varvec{T}_{D}^{N} \) to become the DEMATEL adjusted supermatrix \( \varvec{W}^{*} \) (Table 17)
Step 6 Obtain the final DANP supermatrix by multiplying with itself several times until it converges to \( \varvec{W}^{DANP} \) (the DANP influential weights are shown in Table 4)
Appendix: 2
See Table 18
Appendix: 3
Rights and permissions
About this article
Cite this article
Shen, KY., Sakai, H. & Tzeng, GH. Comparing Two Novel Hybrid MRDM Approaches to Consumer Credit Scoring Under Uncertainty and Fuzzy Judgments. Int. J. Fuzzy Syst. 21, 194–212 (2019). https://doi.org/10.1007/s40815-018-0525-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-018-0525-0