Optimal Design of Adaptive Robust Control for Fuzzy Swarm Robot Systems

Abstract

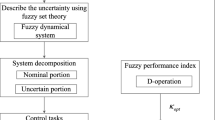
Motion control for an uncertain swarm robot system consisting of N robots is considered. The robots interact with each other through attractions and repulsions, which mimic some biological swarm systems. The uncertainty in the system is possibly fast time varying and bounded with unknown bound, which is assumed to be within a prescribed fuzzy set. On this premise, an adaptive robust control is proposed. Based on the proposed control, an optimal design problem under the fuzzy description of the uncertainty is formulated. This optimal problem is proven to be tractable, and the solution is unique. The solution to this optimal problem is expressed in the closed form. The performance of the resulting control is twofold. First, it assures the swarm robot system deterministic performances (uniform boundedness and uniform ultimate boundedness) regardless of the actual value of the uncertainty. Second, the minimization of a fuzzy-based performance index is assured. Therefore, the optimal design problem of the adaptive robust control for fuzzy swarm robot systems is completely solved.

Appendix

We outline the fuzzy mathematics.

Membership function A function that the values assigned to the elements of the universal set fall within a specified range and indicate the membership grade of these elements in the set in question, is called membership function [22].

Fuzzy set A set $\varOmega$ on the universe of discourse set X is a fuzzy set if the elements of set A are mapped into real numbers in [0, 1] by the membership function $\mu _\varOmega : X\rightarrow [0,1].$

$\alpha$-cut and strong$\alpha$-cut For a given fuzzy set $\varOmega$ defined on X and any number $\alpha \in [0,1]$, the $\alpha$-cut of fuzzy set $\varOmega$ is defined as ${{}^{\alpha }}{\varOmega }=\{x \mid \mu _{\varOmega }(x)\ge \alpha \}$, and the strong $\alpha$-cut of fuzzy set $\varOmega$ is defined as ${{}^{\alpha +}}{\varOmega }=\{x \mid \mu _{\varOmega }(x)> \alpha \}.$

Fuzzy numbers To qualify as a fuzzy number, a fuzzy set $\varOmega$ must possess the following properties: (i) $\varOmega$ is a normal fuzzy set; (ii) $\varOmega$ is convex; (iii) the support of $\varOmega$ must be bounded; (iv) for each $\alpha \in (0, 1]$, ${{}^{\alpha }}{\varOmega }$ is a closed interval in $\mathbf{R}$.

Fuzzy arithmetic Let $\varOmega _1$, $\varOmega _2$ denote two fuzzy numbers, and ${{}^{\alpha }}{\varOmega _{1}}=[a_1, b_1]$, ${{}^{\alpha }}{\varOmega _{2}}=[a_2, b_2]$, $a_1<b_1$, $a_2<b_2$. Then, the fuzzy arithmetic is provided as follows:

$$\begin{aligned}&{{}^{\alpha }}{(\varOmega _1+\varOmega _2)}=[a_1+a_2, b_1+b_2], \end{aligned}$$

(95)

$$\begin{aligned}&{{}^{\alpha }}{(\varOmega _1-\varOmega _2)}=[a_1-b_2, b_1-a_2], \end{aligned}$$

(96)

$$\begin{aligned}&{{}^{\alpha }}{(\varOmega _1\cdot \varOmega _2)}=[\min (a_1a_2, a_1b_2, b_1a_2, b_1b_2), \nonumber \\&\qquad \max (a_1a_2, a_1b_2, b_1a_2, b_1b_2) ],\end{aligned}$$

(97)

$$\begin{aligned}&{{}^{\alpha }}{(\varOmega _1/\varOmega _2)}=[\min (a_1/a_2, a_1/b_2, b_1/a_2, b_1/b_2), \nonumber \\&\qquad \max (a_1/a_2, a_1/b_2, b_1/a_2, b_1/b_2)]. \end{aligned}$$

(98)

Decomposition theorem The fuzzy set $\varTheta$ can be decomposed as

$$\begin{aligned} \varTheta =\bigcup _{\alpha \in [0,1]} {\tilde{\varTheta }}_{\alpha }, \end{aligned}$$

(99)

where $\cup$ is the union of the fuzzy sets (i.e., sup over $\alpha \in [0,1]$), ${\tilde{\varTheta }}_{\alpha }$ is a special fuzzy set on the universe set X defined by the membership function $\mu _{{\tilde{\varTheta }}_{\alpha }} = \alpha I(x)$, the function I(x) is defined as

$$I(x)=\left\{ \begin{array}{ll} 1, &{}\quad {\hbox {if}}\,x\in {{}^{\alpha }}{\varTheta }{}\\ 0,&{}\quad {\hbox {if}}\,x\in {X-{{}^{\alpha }}{\varTheta }{}}. \end{array} \right.$$

(100)