Skip to main content

Advertisement

Springer Nature Link
Log in

Obtaining Efficient Solutions of Interval Multi-objective Linear Programming Problems

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

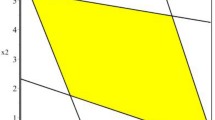
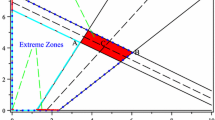
In this paper, we consider interval multi-objective linear programming (IMOLP) models which are used to deal with uncertainties of real-world problems. So far, a variety of approaches for obtaining efficient solutions (ESs) of these problems have been developed. In this paper, we propose a new and two generalized methods. In the new method, converting IMOLP into an interval linear programming (ILP) and then obtaining its optimal solutions (OSs), ESs of the IMOLP are determined. This method has several advantages: (i) This method is the only method which obtains a solution box for IMOLP models. (ii) The solving process is not time consuming. (iii) The number of ESs is higher than for other methods. (V) The method is applicable for large-scale problems. Also, we generalize the \(\varepsilon\)-constraint and lexicographic methods which are used for obtaining ESs of the multi-objective linear programming (MOLP) models which do not have any problems such as lengthy and time-consuming and are applicable for large-scale problems. Some examples were solved to show the efficiency of the proposed methods. Finally, by the proposed method, we solve the IMOLP model corresponding to the problem of the facilities and non-return funds in a bank.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Alefeld, G., Herzberger, J.: Introduction to Interval Computations. Academic Press, New York (1983)

    MATH  Google Scholar 

  2. Allahdadi, M., Deng, C.: An improved three-step method for solving the interval linear programming problem. Yugoslav J. Oper. Res. 28(4), 435–451 (2018)

    Article  MathSciNet  Google Scholar 

  3. Allahdadi, M., Nehi, H.M.: The optimal solutions set of the interval linear programming problems. Optim. Lett. 7, 893–1911 (2013)

    Article  MathSciNet  Google Scholar 

  4. Allahdadi, M., Nehi, H.M.: The optimal value bounds of the objective function in the interval linear programming problem. Chiang Mai. J. Sci. 42(2), 501–511 (2015)

    MATH  Google Scholar 

  5. Allahdadi, M., Nehi, H.M., Ashayerinasab, H.A., Javanmard, M.: Improving the modified interval linear programming method by new techniques. Inf. Sci. 339, 224–236 (2016)

    Article  Google Scholar 

  6. Ashayerinasab, H.A., Nehi, H.M., Allahdadi, M.: Solving the interval linear programming problem: a new algorithm for a general case. Expert Syst. Appl. 93, 39–49 (2018)

    Article  Google Scholar 

  7. Bottea, M., Schöbel, A.: Dominance for multi-objective robust optimization concepts. Eur. J. Oper. Res. 273(2), 430–440 (2019)

    Article  MathSciNet  Google Scholar 

  8. Chinneck, J.W., Ramadan, K.: Linear programming with interval coefficients. J. Oper. Res. Soc. 51, 209–220 (2000)

    Article  Google Scholar 

  9. Dechao Li, L., Leung, Y., Weizhi, W.: Multiobjective interval linear programming in admissible-order vector space. Inf. Sci. 486, 1–19 (2019)

    Article  Google Scholar 

  10. Dourado, A.D.P., Lobato, F.S., Ap Cavalini, A., Steffen, V.: Fuzzy reliability-based optimization for engineering system design. Int. J. Fuzzy Syst. 21(5), 1418–1429 (2019)

    Article  Google Scholar 

  11. Ehrgott, M.: Multicriteria Optimization. Springer, Berlin (2005)

    MATH  Google Scholar 

  12. Garajová, E., Hladík, M., Rada, M.: The effects of transformations on the optimal set in interval linear programming, In: Proceedings of the 14th international symposium on operational research, SOR’17, Bled, Slovenian Society Informatika, Ljubljana, Slovenia, pp. 487–492 (2017)

  13. Hladík, M.: Complexity of necessary efficiency in interval linear programming and multiobjective linear programming. Optim. Lett. 6(5), 893–899 (2012)

    Article  MathSciNet  Google Scholar 

  14. Hladík, M.: How to determine basis stability in interval linear programming. Optim. Lett. 8, 375–389 (2014)

    Article  MathSciNet  Google Scholar 

  15. Hladík, M.: Interval linear programming: a survey. In: Mann, Z.A. (ed.) Linear Programming, New Frontiers in Theory and Applications, Chapter 2, pp. 85–120. Nova Science Publishers, New York (2012)

    Google Scholar 

  16. Hladík, M.: One necessarily efficient solutions in interval multi objective linear programming, Proceedings of the 25th Mini-EURO Conference Uncertainty and Robustness in Planning and Decision Making URPDM 2010, pp. 1–10. Coimbra, Portugal (2010)

  17. Hladík, M.: Weak and strong solvability of interval linear systems of equations and inequalities. Linear Algebra Appl. 438(11), 4156–4165 (2013)

    Article  MathSciNet  Google Scholar 

  18. Huang, G.H., Baetz, B.W., Patry, G.G.: Grey integer programming: an application to waste management planning under uncertainty. Eur. J. Oper. Res. 83, 594–620 (1995)

    Article  Google Scholar 

  19. Huang, G.H., Moore, R.D.: Grey linear programming, its solving approach, and its application. Int. J. Syst. Sci. 24, 159–172 (1993)

    Article  MathSciNet  Google Scholar 

  20. Inuiguchi, M.: Necessary efficiency is partitioned into possible an necessary optimalities, IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), pp. 209–214. Edmonton, AB, Canada (2013)

  21. Inuiguchi, M., Kume, Y.: Goal programming approach for solving IMOLP problems. Eur. J. Oper. Res. 52, 345–360 (1991)

    Article  Google Scholar 

  22. Inuiguchi, M., Sakawa, M.: An achievement rate approach to linear programming problems with an interval objective function. J. Oper. Res. Soc. 48, 25–33 (1997)

    Article  Google Scholar 

  23. Inuiguchi, M., Sakawa, M.: Minimax regret solution to multi objective linear programming problems with interval objective function coefficients. Eur. J. Oper. Res. 86, 526–536 (1995)

    Article  Google Scholar 

  24. Inuiguchi, M., Sakawa, M.: Possible and necessary efficiency in possibilistic multiobjective linear programming problems and possible efficiency test. Fuzzy Sets Syst. 78, 321–341 (1996)

    Article  MathSciNet  Google Scholar 

  25. Koníčková, J.: Sufficient condition of basis stability of an interval linear programming problem. ZAMM. Z. Angew. Math. Mech. 81(3), 677–678 (2001)

    Article  Google Scholar 

  26. Mishmast Nehi, H., Ashayerinasab, H.A., Allahdadi, M.: Solving methods for interval linear programming problem: a review and an improved method. Oper. Res. (2018). https://doi.org/10.1007/s12351-018-0383-4

    Article  Google Scholar 

  27. Oliveira, C., Antunes, C.H.: Multiple objective linear programming models with interval coefficient-an illustrated overview. Eur. J. Oper. Res. 181, 1434–1463 (2007)

    Article  Google Scholar 

  28. Razavi Hajiagha, S.H.: Programming with interval multi-objective linear coefficients: a fuzzy set based approach. Kybernetes 42(3), 482–496 (2013)

    Article  MathSciNet  Google Scholar 

  29. Rex, J., Rohn, J.: Sufficient conditions for regularity and singularity of interval matrices. SIAM J. Matrix Anal. Appl. 20(2), 437–445 (1998)

    Article  MathSciNet  Google Scholar 

  30. Rivaz, S., Yaghoobi, M.A.: Minimax regret solution to linear programming problems with an interval objective function. Eur. J. Oper. Res. 21(3), 625–649 (2013)

    Article  MathSciNet  Google Scholar 

  31. Rivaz, S., Yaghoobi, M.A.: Weighted sum of maximum regrets in an interval MOLP problem. Int. Trans. Oper. Res. 25(5), 1659–1676 (2015)

    Article  MathSciNet  Google Scholar 

  32. Rivaz, S., Yaghoobi, M.A., Hladík, M.: Using modified maximum regret for finding a necessarily efficient solution in an interval MOLP problem. Fuzzy Optim. Decis. Mak. 15(3), 237–253 (2016)

    Article  MathSciNet  Google Scholar 

  33. Rohn, J.: Cheap and tight bound: the recent result by E. Hansen can be made more efficient. Interval Comput. 4, 13–21 (1993)

    MathSciNet  MATH  Google Scholar 

  34. Rohn, J.: Forty necessary and sufficient conditions for regularity of interval matrices: a survey. Electron J. Linear Algebra 18, 500–512 (2009)

    MathSciNet  MATH  Google Scholar 

  35. Steuer, R.E.: Multiple criteria optimization: theory, computation and application. Wiley, New York (1989)

    MATH  Google Scholar 

  36. Tong, S.C.: Interval number, fuzzy number linear programming. Fuzzy Sets Syst. 66, 301–306 (1994)

    Article  MathSciNet  Google Scholar 

  37. Wang, X., Huang, G.: Violation analysis on two-step method for interval linear programming. Inf. Sci. 281, 85–96 (2014)

    Article  MathSciNet  Google Scholar 

  38. Xu, J., Fang, H., Zeng, F., Chen, Y.H., Guo, H.: Robust observer design and fuzzy optimization for uncertain dynamic systems. Int. J. Fuzzy Syst. 21(5), 1511–1523 (2019).

    Article  MathSciNet  Google Scholar 

  39. Yang, Y., Zhao, J., Xia, J., Zhuang, G., Zhang, W.: Multiobjective optimization control for uncertain nonlinear stochastic system with state-delay. Int. J. Fuzzy Syst. 21(1), 72–83 (2019).

    Article  MathSciNet  Google Scholar 

  40. Zhou, F., Huang, G.H., Chen, G., Guo, H.: Enhanced-interval linear programming. Eur. J. Oper. Res. 199, 323–333 (2009)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

M. Hladík was supported by the Czech Science Foundation Grant P403-19-02773S.

Author information

Authors and Affiliations

  1. Mathematics Faculty, University of Sistan and Baluchestan, Zahedan, Iran

    Aida Batamiz & Mehdi Allahdadi

  2. Department of Applied Mathematics, Charles University, Prague, Czech Republic

    Milan Hladík

  3. Department of Econometrics, University of Economics, nam. W. Churchilla 4, 13067, Prague, Czech Republic

    Milan Hladík

Authors
  1. Aida Batamiz
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mehdi Allahdadi
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Milan Hladík
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mehdi Allahdadi.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Batamiz, A., Allahdadi, M. & Hladík, M. Obtaining Efficient Solutions of Interval Multi-objective Linear Programming Problems. Int. J. Fuzzy Syst. 22, 873–890 (2020). https://doi.org/10.1007/s40815-020-00800-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-020-00800-5

Keywords