Skip to main content

Advertisement

Springer Nature Link
Log in

A New Fuzzy PID Control System Based on Fuzzy PID Controller and Fuzzy Control Process

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

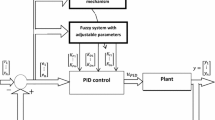
In this paper, we present a fuzzy PID control system as a combination of a fuzzy PID controller and a fuzzy control process, which is represented by a fuzzy control differential equation in linear form. We use the concepts of the generalized Hukuhara differentiability and the fuzzy integral of fuzzy-valued functions to study some qualitative properties for this system in the space of fuzzy numbers. We also study the existence and uniqueness result for solutions of fuzzy PID control differential equations under some suitable conditions. A number of examples are also provided to illustrate the results of the theory.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Availability of data and materials

All data generated or analyzed during this study are included in this article.

References

  1. Bede, B.: Mathematics of Fuzzy Sets and Fuzzy Logic. Springer-Verlag, Berlin (2013)

    Book  Google Scholar 

  2. Bede, B., Gal, S.G.: Generalizations of the differentiability of fuzzy-number-valued functions with applications to fuzzy differential equations. Fuzzy. Sets. Syst. 151, 581–599 (2005)

    Article  MathSciNet  Google Scholar 

  3. Bede, B.: A note on two-point boundary value problems associated with non-linear differential equations. Fuzzy. Sets. Syst. 157, 986–989 (2006)

    Article  MathSciNet  Google Scholar 

  4. Bede, B., Gal, S.G.: Solutions of fuzzy differential equations based on generalized differentiability. Commun. Math. Anal. 9, 22–41 (2010)

    MathSciNet  MATH  Google Scholar 

  5. Bede, B., Stefanini, L.: Generalized differentiability of fuzzy-valued functions. Fuzzy. Sets. Syst. 230, 119–141 (2013)

    Article  MathSciNet  Google Scholar 

  6. Chalco-Cano, Y., Roman-Flores, H.: On new solutions of fuzzy differential equations. Chaos. Solitons. Fractals. 38, 112–119 (2008)

    Article  MathSciNet  Google Scholar 

  7. Chang, S.L., Zadeh, L.: On fuzzy mapping and control. IEEE. Transact. Syst. Man. Cybern. 2, 30–34 (1972)

    Article  MathSciNet  Google Scholar 

  8. Dubois, D., Prade, H.: Towards fuzzy differential calculus-part III: differentiation. Fuzzy. Sets. Syst. 8, 225–233 (1982)

    Article  Google Scholar 

  9. Goetschel, R., Voxman, W.: Elementary fuzzy calculus. Fuzzy. Sets. Syst. 18, 31–43 (1986)

    Article  MathSciNet  Google Scholar 

  10. Stefanini, L., Sorini, L., Guerra, M.L.: Parametric representation of fuzzy numbers and application to fuzzy calculus. Fuzzy. Sets. Syst. 157, 2423–2455 (2006)

    Article  MathSciNet  Google Scholar 

  11. Sari, N.N., Jahanshahi, H., Fakoor, M.: Adaptive fuzzy PID control strategy for spacecraft attitude control. Int. J. Fuzzy. Syst. 21, 769–781 (2019)

    Article  MathSciNet  Google Scholar 

  12. Tsai, C., Tai, F., Chang, Y.: Chia-Ta Tsai, adaptive predictive PID control using fuzzy wavelet neural networks for nonlinear discrete-time time-delay systems. Int. J. Fuzzy. Syst. 19, 1718–1730 (2017)

    Article  MathSciNet  Google Scholar 

  13. Tsai, C., Yu, C., Tsai, C.: Adaptive ORFWNN-based predictive PID control. Int. J. Fuzzy. Syst. 21, 1544–1559 (2019)

    Article  MathSciNet  Google Scholar 

  14. Hukuhara, M.: Integration des applications mesurables dont la valeur est uncompact convexe. Funkcialaj Ekvacioj 10, 205–223 (1967)

    MathSciNet  MATH  Google Scholar 

  15. Kandel, A., Byatt, W.J.: Fuzzy differential equations, In Proceeding of the International Conference on Cybernetics and Society, pp. 1213–1216. Japan, Tokyo (1978)

  16. Lakshmikantham, V., Mohapatra, R.N.: Theory of fuzzy differential equations and inclusions. Taylor & Francis, London (2003)

    Book  Google Scholar 

  17. Lv, X., Fei, J., Sun, Y.: Fuzzy PID controller design for uncertain networked control systems based on T-S fuzzy model with random delays. Int. J. Fuzzy. Syst. 21, 571–582 (2019)

    Article  MathSciNet  Google Scholar 

  18. Mizumoto, M.: Realization of PID controls by fuzzy control methods. Fuzzy Sets and Systems 70, 171–182 (1995)

    Article  MathSciNet  Google Scholar 

  19. Moore, R.E., Kearfott, R.B., Cloud, M.J.: Introduction to Interval Analysis. Society For Industrial And Applied Mathematics Philadelphia, SIAM (2009)

  20. Negoita, C., Ralescu, D.: Applications of Fuzzy Sets to System Analysis. Wiley, New York (1975)

    Book  Google Scholar 

  21. Phu, N.D.: On nonlocal initial problems for fuzzy differential equations and environmental pollution problems. Acad. J. Appl. Math. Sci. 2, 77–92 (2016)

    Google Scholar 

  22. Phu, N.D., Dzung, L.Q.: On the stability and controllability of fuzzy control set differential equations. Int. J. Reliab. Saf. 5, 320–335 (2011)

    Article  Google Scholar 

  23. Phu, N.D., Hung, N.N.: Minimum stability control problem and time-optimal control problem for fuzzy linear control systems. Fuzzy. Sets. Syst. 371, 1–24 (2019)

    Article  MathSciNet  Google Scholar 

  24. Phu, N.D., Tri, P.V., Ahmadian, A., Salahshour, S., Baleanu, D.: Some kinds of the controllable problems for fuzzy control dynamic systems. J. Dyn. Syst. Meas. Control. (2018). https://doi.org/10.1115/1.4039484

    Article  Google Scholar 

  25. Puri, M.L., Ralescu, D.: Differential for fuzzy function. J. Math. Anal. Appl. 91, 552–558 (1983)

    Article  MathSciNet  Google Scholar 

  26. Zadeh, L.A.: Fuzzy sets. Inform. Control. 8, 338–353 (1965)

    Article  Google Scholar 

  27. Zhao, ZY., Tomizuka, M., lsaka, S.: Fuzzy gain scheduling of PID controllers. J. IEEE. Transact. Syst. Man. Cybern. 23, 1302–1308 (1993)

    Article  Google Scholar 

  28. Zhao, T., Chen, Y., Dian, S., Guo, R., Li, S.: General type-2 fuzzy gain scheduling PID controller with application to power-line inspection robots. Int. J. Fuzzy. Syst. 22, 181–200 (2020)

    Article  Google Scholar 

Download references

Acknowledgements

The authors are very grateful to the anonymous reviewers, associate editor, and editor for their insightful and constructive suggestions that have led to an improved version of this manuscript.

Author information

Authors and Affiliations

  1. Faculty of Engineering Technology, Quang Trung University, Quy Nhon City, Vietnam

    Nguyen Dinh Phu & Nguyen Nhut Hung

  2. Institute of IR 4.0, The National University of Malaysia, 43600 UKM, Bangi, Selangor, Malaysia

    Ali Ahmadian

  3. Institute for Mathematical Research (INSPEM), University Putra Malaysia, 43400 UPM, Serdang, Selangor, Malaysia

    Norazak Senu

Authors
  1. Nguyen Dinh Phu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Nguyen Nhut Hung
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Ali Ahmadian
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Norazak Senu
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

The authors declare that the paper was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.

Corresponding author

Correspondence to Ali Ahmadian.

Ethics declarations

Competing interests

The authors declare that they have no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Phu, N.D., Hung, N.N., Ahmadian, A. et al. A New Fuzzy PID Control System Based on Fuzzy PID Controller and Fuzzy Control Process. Int. J. Fuzzy Syst. 22, 2163–2187 (2020). https://doi.org/10.1007/s40815-020-00904-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-020-00904-y

Keywords