Distance-Based Large-Scale Group Decision-Making Method with Group Influence

Abstract

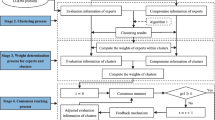
Large-scale group decision making (LSGDM), which involves a large number of decision makers, has become a hot topic in the field of decision making. To address LSGDM problems with hesitant information, in this paper, a distance-based LSGDM method is proposed by considering group influence. In the method, a generalized distance measure between two pieces of hesitant information is designed to overcome the limitations of existing distance measures. To accelerate the convergence of consensus reaching process with the consideration of the interaction among decision makers, decision makers are divided into several subgroups. The group leader is selected in terms of the contributions of decision makers to group consensus. In order to help generate a satisfactory solution by adequately considering the decision makers’ diverse opinions, the group discussion is introduced to clarify their opinions and minimize bias under the organization of the selected group leader. Based on the changes in the preference information before and after group discussion, the influence of each subgroup is generated and further applied to determine the weights of subgroups. Simulation and comparison experiments are conducted to demonstrate the applicability and effectiveness of the proposed method.

Appendix: Proof of Theorem 1

Theorem 1

Suppose that $h_{ 1} = \{ \gamma_{ 1 1} , \ldots ,\gamma_{{1l(h_{1} )}} \}$ and $h_{2} = \{ \gamma_{ 2 1} , \ldots ,\gamma_{{ 2l(h_{2} )}} \}$ are two HFEs. The proposed distance measure between h₁ and h₂ in Eq. (11), i.e., d_g(h₁, h₂), satisfies the following properties:

• (1) Boundedness: 0 ≤ d_g(h₁, h₂) ≤ 1.

• (2) Commutativity: d_g(h₁, h₂) = d_g(h₂, h₁).

• (3) Reflexivity: d_g(h₁, h₂) = 0 iff h₁ = h₂.

Proof

(1) It can be deduced from Definition 8 that

$$d_{g} (h_{1} ,h_{2} ) = \left[ {\frac{1}{{l(h_{1} )l(h_{2} )}}\left( {\sum\limits_{j = 1}^{{l(h_{1} )}} {\sum\limits_{k = 1}^{{l(h_{2} )}} {\left( {\gamma_{1\sigma (j)} - \gamma_{2\sigma (k)} } \right)^{\lambda } } } - \sum\limits_{j = 1}^{{l(h_{ \cap } )}} {\sum\limits_{k = 1}^{{l(h_{ \cap } )}} {\left( {\gamma_{ \cap \sigma (j)} - \gamma_{ \cap \sigma (k)} } \right)^{\lambda } } } } \right)} \right]^{1/\lambda } .$$

From $0 \le \gamma_{1\sigma (j)} ,\gamma_{2\sigma (k)} ,\gamma_{ \cap \sigma (j)} ,\gamma_{ \cap \sigma (k)} \le 1$ and $1\le \lambda \le + \infty$, it can be known that

$$\sum\limits_{j = 1}^{{l(h_{1} )}} {\sum\limits_{k = 1}^{{l(h_{2} )}} {\left( {\gamma_{1\sigma (j)} - \gamma_{2\sigma (k)} } \right)^{\lambda } } } \in [0,1]\;{\text{and}}\;\sum\limits_{j = 1}^{{l(h_{ \cap } )}} {\sum\limits_{k = 1}^{{l(h_{ \cap } )}} {\left( {\gamma_{ \cap \sigma (j)} - \gamma_{ \cap \sigma (k)} } \right)^{\lambda } } } \in [0,1].$$

Meanwhile, h_∩ = h₁∩h₂ indicates that

$$\sum\limits_{j = 1}^{{l(h_{1} )}} {\sum\limits_{k = 1}^{{l(h_{2} )}} {\left( {\gamma_{1\sigma (j)} - \gamma_{2\sigma (k)} } \right)^{\lambda } } } \ge \sum\limits_{j = 1}^{{l(h_{ \cap } )}} {\sum\limits_{k = 1}^{{l(h_{ \cap } )}} {\left( {\gamma_{ \cap \sigma (j)} - \gamma_{ \cap \sigma (k)} } \right)^{\lambda } } } .$$

In particular, when h₁ = h₂, i.e., h_∩ = h₁ = h₂, we have $\sum\nolimits_{j = 1}^{{l(h_{1} )}} {\sum\nolimits_{k = 1}^{{l(h_{2} )}} {\left( {\gamma_{1\sigma (j)} - \gamma_{2\sigma (k)} } \right)^{\lambda } } } = \sum\nolimits_{j = 1}^{{l(h_{ \cap } )}} {\sum\nolimits_{k = 1}^{{l(h_{ \cap } )}} {\left( {\gamma_{ \cap \sigma (j)} - \gamma_{ \cap \sigma (k)} } \right)^{\lambda } } }$ and further d_g(h₁, h₂) = 0. When (h₁, h₂) = ({0}, {1}) or (h₁, h₂) = ({1}, {0}), we have d_g(h₁, h₂) = 1.

Therefore, it can be further deduced that 0 ≤ d_g(h₁, h₂) ≤ 1, which indicates that Boundedness is verified.

(2) According to Eq. (11), we have

$$d_{g} (h_{1} ,h_{2} ) = \left[ {\frac{1}{{l(h_{1} )l(h_{2} )}}\left( {\sum\limits_{j = 1}^{{l(h_{1} )}} {\sum\limits_{k = 1}^{{l(h_{2} )}} {\left( {\gamma_{1\sigma (j)} - \gamma_{2\sigma (k)} } \right)^{\lambda } } } - \sum\limits_{j = 1}^{{l(h_{ \cap } )}} {\sum\limits_{k = 1}^{{l(h_{ \cap } )}} {\left( {\gamma_{ \cap \sigma (j)} - \gamma_{ \cap \sigma (k)} } \right)^{\lambda } } } } \right)} \right]^{1/\lambda } ,$$

and $d_{g} (h_{2} ,h_{1} ) = \left[ {\frac{1}{{l(h_{2} )l(h_{1} )}}\left( {\sum\limits_{j = 1}^{{l(h_{2} )}} {\sum\limits_{k = 1}^{{l(h_{1} )}} {\left( {\gamma_{2\sigma (j)} - \gamma_{1\sigma (k)} } \right)^{\lambda } } } - \sum\limits_{j = 1}^{{l(h_{ \cap } )}} {\sum\limits_{k = 1}^{{l(h_{ \cap } )}} {\left( {\gamma_{ \cap \sigma (j)} - \gamma_{ \cap \sigma (k)} } \right)^{\lambda } } } } \right)} \right]^{1/\lambda } .$

Because h₁ ∩ h₂ = h₂ ∩ h₁, d_g(h₁, h₂) = d_g(h₂, h₁) clearly holds.

As a whole, Commutativity is verified.

(3) First, suppose that h₁ = h₂. Under the conditions, we have h_∩ = h₁ = h₂. According to Eq. (11), it can be obtained that d_g(h₁, h₂) = 0.

Second, suppose that d_g(h₁, h₂) = 0. Under the conditions, it can be deducted from Eq. (11) that $\sum\nolimits_{j = 1}^{{l(h_{1} )}} {\sum\nolimits_{k = 1}^{{l(h_{2} )}} {\left( {\gamma_{1\sigma (j)} - \gamma_{2\sigma (k)} } \right)^{\lambda } } } = \sum\nolimits_{j = 1}^{{l(h_{ \cap } )}} {\sum\nolimits_{k = 1}^{{l(h_{ \cap } )}} {\left( {\gamma_{ \cap \sigma (j)} - \gamma_{ \cap \sigma (k)} } \right)^{\lambda } } }$. Through synthetically considering this equation and h_∩= h₁∩h₂, it can be concluded that h_∩ = h₁ = h₂, i.e., h₁ = h₂.

As a whole, Reflexivity is verified.

The above analyses validate Theorem 1. □