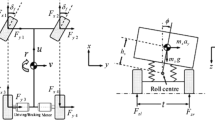
Abstract
Robustness is a major concern when engineers design lateral stability controllers for intelligent vehicles. The system uncertainty derives from the internal parametric perturbation and the external disturbance. The fuzzy set theory is adopted to describe the bound of the uncertainty. Hence the vehicle lateral dynamical system becomes a fuzzy dynamical system. An explicit robust optimal control law is then proposed to ensure the uniform boundedness and uniform ultimate boundedness of the system. The control law is deterministic and is not IF-THEN fuzzy rule based. A two-player cooperative game is established to determine the optimal value of tunable parameters. The cost functions of the players are developed based on the system performance and the control cost. The Pareto optimal is then obtained using the cooperative game theory. The effectiveness of the proposed method is proven by numerical simulations and Hardware-in-the-loop (HIL) experiments. This paper makes a breakthrough by casting the cooperative game theory and the fuzzy set theory into vehicle lateral stability control.









Similar content being viewed by others
References
Moradi-Pari, E., Mahjoub, H., Kazemi, H., et al.: Utilizing model-based communication and control for cooperative automated vehicle applications. IEEE Trans. Intell. Veh. 2(1), 38–51 (2017)
Li, S., Yang, Y., Li, K., et al.: Dynamical modeling and distributed control of connected and automated vehicles: challenges and opportunities. IEEE Trans. Intell. Transp. Syst. 9(3), 46–58 (2017)
Attia, R., Orjuela, R., Basset, M.: Combined longitudinal and lateral control for automated vehicle guidance. Veh. Syst. Dynam. 52(2), 261–279 (2014)
Wei, S., Zou, Y., Zhang, X., et al.: An integrated longitudinal and lateral vehicle following control system with radar and vehicle-to-vehicle communication. IEEE Trans. Veh. Tech. 68(2), 1116–1127 (2019)
Nahidi, A., Kasaiezadeh, A., Khosravani, S., et al.: Modular integrated longitudinal and lateral vehicle stability control for electric vehicles. Mechatronics 44, 60–70 (2017)
Zhang, L., Wang, Y., Wang, Z.: Robust lateral motion control for in-wheel-motor-drive electric vehicles with network induced delays. IEEE Trans. Veh. Tech. 68(11), 10585–10593 (2019)
Song, Y., Chen, H., Li, D.: Virtual-point-based fault-tolerant lateral and longitudinal control of 4W-steering vehicles. IEEE Trans. Intell. Transp. Syst. 12(4), 1343–1351 (2011)
Han, G., Fu, W., Wang, W., et al.: The lateral tracking control for the intelligent vehicle based on adaptive PID neural network. Sensors 17(6), 1244–1258 (2017)
Wang, R., Sun, Y., Lin, M., et al.: Research on bus roll stability control based on LQR. In: 2015 International Conference Intelligent Transportation, Vietnam, pp. 622–625 (2015)
Shi, K., Yuan, X., Huang, G., et al.: DLMPCS-based improved yaw stability control strategy for DDEV. IET Intell. Trans. Syst. 13(9), 1329–1339 (2019)
Wu, H., Li, Y.: Coordination Control of Path Tracking and Stability for 4WS Autonomous Vehicle. In: 2020 International Conference Electromechanical Control Technology Transporation, China, pp. 343–348 (2020)
Chen, C., Jia, Y., Shu, M., et al.: Hierarchical adaptive path tracking control for autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 16(5), 2900–2912 (2015)
Wang, F., Chen, H., Guo, K.H., et al.: A novel integrated approach for path following and directional stability control of road vehicles after a tire blow-out. Mech. Syst. Signal Process. 93, 431–444 (2017)
Ji, Xuewu, He, Xiangkun, Lv, Chen, et al.: A vehicle stability control strategy with adaptive neural network sliding mode theory based on system uncertainty approximation. Veh. Syst. Dyn 56(6), 923–946 (2018)
Zhang, H., Wang, J.: Vehicle lateral dynamics control through AFS/DYC and robust gain-scheduling approach. IEEE Trans. Veh. Technol. 65(1), 489–494 (2016)
Zhao, W., Qin, X., Wang, C.: Yaw and lateral stability control for four-wheel steer-by-wire system. IEEE/ASME Trans. Mechatron. 23(6), 2628–2637 (2018)
Lee, S., Chung, C.: Predictive control with sliding mode for autonomous driving vehicle lateral maneuvering. American Control Conference, pp. 2998–3003 (2017)
Cheng, S., Li, L., Liu, C., et al.: Robust LMI-based H-infinite controller integrating AFS and DYC of autonomous vehicles with parametric uncertainties. IEEE Trans. Syst. Man Cybern. Syst. (2020). http://https://doi.org/10.1109/TSMC.2020.2964282
Zhang, H., Zhao, W.: Stability control strategy of steer-by-wire system based on LQG/LTR. Sci. China Technol. Sci. 60(6), 844–853 (2017)
Lee, K., Jeon, S., Kim, H., et al.: Optimal path tracking control of autonomous vehicle: adaptive full-state linear quadratic gaussian (LQG) control. IEEE Access 7, 109120–109133 (2019)
Kalman, R.E.: Probability in the real world as a system attribute. Quart. Cent. Wiskd. Inform. 9, 181–203 (1996)
Pincus, S., Kalman, R.E.: Not all (possibly) random sequences are created equal. Proc. Natl. Acad. Sci. 94(8), 3513–3518 (1997)
Krishna, S., Narayanan, S., Denis, A.S.: Fuzzy logic based yaw stability control for active front steering of a vehicle. J. Mech. Sci. Technol. 28(12), 5169–5174 (2014)
Jin, X., Yu, Z., Yin, G., et al.: Improving vehicle handling stability based on combined AFS and DYC system via robust Takagi-Sugeno fuzzy control. IEEE Trans. Intell. Transp. Syst. 19(8), 2696–2707 (2018)
Hu, X., Wu, L., Hu, C., et al.: Dynamic output feedback control of a flexible air-breathing hypersonic vehicle via T-S fuzzy approach. Int. J. Syst. Sci. 45(8), 1740–1756 (2014)
Geng, C., Mostefai, L., Denai, M., et al.: Direct yaw-moment control of an in-wheel-motored electric vehicle based on body slip angle fuzzy observer. IEEE Trans. Ind. Electron. 56(5), 1411–1419 (2009)
Zadeh, L.A.: Fuzzy sets. Inf. Control 8(3), 338–353 (1965)
Zimmermann, H.J.: Fuzzy Set Theory and Its Applications. Springer Science & Business Media, Berlin (2011)
Hu, C., Wang, R., Yan, F., et al.: Differential steering based yaw stabilization using ISMC for independently actuated electric vehicles. IEEE Trans. Intell. Transp. Syste. 19(2), 627–638 (2018)
Huang, D., Zhai, J., Ai, W., et al.: Disturbance observer-based robust control for trajectory tracking of wheeled mobile robots. Neurocomputing 198, 74–79 (2016)
Ji, X., He, X., Lv, C., et al.: A vehicle stability control strategy with adaptive neural network sliding mode theory based on system uncertainty approximation. Veh. Syst. Dyn. (2018). https://doi.org/10.1080/00423114.2017.1401100
Ji, X., Liu, Y., Yang, K., et al.: Interactive control paradigm-based robust lateral stability controller design for autonomous automobile path tracking with uncertain disturbance: a dynamic game approach. IEEE Trans. Veh. Technol. 67(8), 6906–6920 (2018)
Xu, J., Du, Y., Chen, Y.H., et al.: Optimal robust control design for constrained uncertain systems: a fuzzy-set theoretic approach. IEEE Trans. Fuzzy Syst. 26(6), 3494–3505 (2018)
Danielsen, L.E., Parker, M.G., Sole, P.: The Rayleigh Quotient of Bent Functions. Springer, Berlin (1985)
Chen, Y.H.: A new approach to the control design of fuzzy dynamical systems. J. Dyn. Syst. Meas. Control 45(5), 1527–1542 (1987)
Mariano, J., Amelia, B.: Pareto-Optimal Solutions in Fuzzy Multi-Objective Linear Programming. Elsevier, North-Holland (2009)
Hale, J.K.: Ordinary Differential Equations. Dover Publications, New York (2009)
Horn, R.A., Johnson, C.R.: Matrix Analysis. Cambridge University Press, England (1985)
Acknowledgements
This research is sponsored in part by the NSFC Program (No. 61872217, No. U1701262, No. U1801263), the research is also sponsored in part by the Guangdong Provincial Key Laboratory of Cyber-Physical Systems, as well as be sponsored in part by the Industrial Internet innovation and development project of ministry of industry and information technology.
Author information
Authors and Affiliations
Corresponding author
Appendix: Derivative Cost Functions Using D Operator
Appendix: Derivative Cost Functions Using D Operator
As mentioned in Sect. 4, the cost function should be deterministic to formulate the cooperative game. Therefore, we introduce the D operator to form the mapping from fuzzy set to real number.
Definition 2
Consider a fuzzy set
For any function \(f:\Xi \rightarrow {\mathbb {R}}\), the D operation \(D[f(\xi )]\) is given by
According to definition 2, the D operator can be viewed as a defuzzification method and has the follow properties
The transient state and steady state system performance can be derived as follows
Based on Eqs. (77)–(80), we now propose the explicit cost functions for the two-player cooperative game
We denote
Then we have
Rights and permissions
About this article
Cite this article
Hu, Z., Huang, J., Yan, Z. et al. Cooperative-Game-Oriented Optimal Design in Vehicle Lateral Stability Control with Fuzzy Uncertainties. Int. J. Fuzzy Syst. 24, 867–882 (2022). https://doi.org/10.1007/s40815-021-01160-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-021-01160-4