Skip to main content
Springer Nature Link
Log in

A Fuzzy Decision-Theoretic Rough Set Approach for Type-2 Fuzzy Conditional Information Systems and Its Application in Decision-Making

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

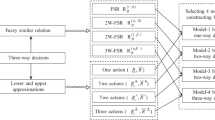
The decision-theoretic rough set model based on Bayesian decision theory proposes a framework for studying rough set approximations using probabilistic theory, it has become an important research direction of rough set theory. In order to extend the theory of decision-theoretic rough set, this article is devoted to studying the fuzzy decision-theoretic rough set model in type-2 fuzzy conditional information systems. The type-2 fuzzy similarity relations are induced though computing the measure of similarity between objects for each attribute. Then, we use intersection operation of type-2 fuzzy sets to aggregate the multiple induced fuzzy similarity relations. Next, a fuzzy decision-theoretic rough set approach for type-2 fuzzy conditional information systems is proposed by means of inclusion degree of type-2 fuzzy sets. Finally, an example is considered to illustrate the effectiveness of the proposed method, which is helpful for applying these theories to deal with practical issues.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Pawlak, Z.: Rough sets. Int. J. Comput. Inf. Sci. 11(5), 341–356 (1982)

    MATH  Google Scholar 

  2. Pawlak, Z.: Rough sets: theoretical aspect of reasoning about data. Kluwer Academic Publishers, New York (1991)

    MATH  Google Scholar 

  3. Dai, J.H., Wei, B.J., Zhang, X.H., Zhang, Q.L.: Uncertainty measurement for incomplete interval-valued information systems based on \(\alpha\)-weak similarity. Knowl. Based Syst. 136, 159–171 (2017)

    Google Scholar 

  4. Du, Y., Hu, Q.H., Zhu, P.F., Ma, P.J.: Rule learning for classification based on neighborhood covering reduction. Inf. Sci. 181(24), 5457–5467 (2011)

    MathSciNet  Google Scholar 

  5. Dai, J.H., Tian, H.W., Wang, W.T., Liu, L.: Decision rule mining using classification consistency rate. Knowl. Based Syst. 43, 95–102 (2013)

    Google Scholar 

  6. Wei, J.M., Wang, S.Q., Yuan, X.J.: Ensemble rough hypercuboid approach for classifying cancers. IEEE Trans. Knowl. Data Eng. 22(3), 381–391 (2010)

    Google Scholar 

  7. Dai, J.H., Hu, Q.H., Zhang, J.H., Hu, H., Zheng, N.G.: Attribute selection for partially labeled categorical data by rough set approach. IEEE Trans. Cybern. 47(9), 2460–2471 (2017)

    Google Scholar 

  8. Dai, J.H., Hu, H., Wu, W.Z., Qian, Y.H., Huang, D.B.: Maximal-discernibility-pair-based approach to attribute reduction in fuzzy rough sets. IEEE Trans. Fuzzy Syst. 26(4), 2174–2187 (2018)

    Google Scholar 

  9. Dai, J.H., Hu, Q.H., Hu, H., Huang, D.B.: Neighbor inconsistent pair selection for attribute reduction by rough set approach. IEEE Trans Fuzzy Syst. 26(2), 937–950 (2018)

    Google Scholar 

  10. Wang, C.Z., Shi, Y.P., Fan, X.D., Shao, M.W.: Attribute reduction based on \(k\)-nearest neighborhood rough sets. Int. J. Approx. Reason. 106, 18–31 (2019)

    MathSciNet  MATH  Google Scholar 

  11. Dai, J.H., Xu, Q.: Attribute selection based on information gain ratio in fuzzy rough set theory with application to tumor classification. Appl. Soft Comput. 13(1), 211–221 (2013)

    Google Scholar 

  12. Dai, J.H., Chen, J.L.: Feature selection via normative fuzzy information weight with application into tumor classification. Appl. Soft Comput. 92, 106299 (2020)

    Google Scholar 

  13. Qian, Y.H., Liang, J.Y., Wu, W.Z., Dang, C.Y.: Information granularity in fuzzy binary GrC model. IEEE Trans. Fuzzy Syst. 19(2), 253–264 (2011)

    Google Scholar 

  14. Chen, H.M., Li, T.R., Luo, C., Horng, S.-J., Wang, G.Y.: A decision-theoretic rough set approach for dynamic data mining. IEEE Trans. Fuzzy Syst. 23(6), 1958–1970 (2015)

    Google Scholar 

  15. Zhang, K., Zhan, J.M., Yao, Y.Y.: TOPSIS method based on a fuzzy covering approximation space: an application to biological nano-materials selection. Inf. Sci. 502, 297–329 (2019)

    Google Scholar 

  16. Zhang, K., Zhan, J.M., Wu, W.Z.: On multi-criteria decision-making method based on a fuzzy rough set model with fuzzy \(\alpha\)-neighborhoods. IEEE Trans. Fuzzy Syst. (2020). https://doi.org/10.1109/TFUZZ.2020.3001670

    Article  Google Scholar 

  17. Dubois, D., Prade, H.: Rough fuzzy sets and fuzzy rough sets. Int. J. Gen. Syst. 17(2), 191–209 (1990)

    MATH  Google Scholar 

  18. Yue, X.D., Chen, Y.F., Miao, D.Q., Qian, J.: Tri-partition neighborhood covering reduction for robust classification. Int. J. Approx. Reason. 83, 371–384 (2017)

    MathSciNet  MATH  Google Scholar 

  19. Wang, C.Z., Huang, Y., Shao, M.W., Fan, X.D.: Fuzzy rough set-based attribute reduction using distance measures. Knowl. Based Syst. 164, 205–212 (2019)

    Google Scholar 

  20. Ziarko, W.: Variable precision rough set model. J. Comput. Syst. Sci. 46(1), 39–59 (1993)

    MathSciNet  MATH  Google Scholar 

  21. Slezak, D., Ziarko, W.: The investigation of the Bayesian rough set model. Int. J. Approx. Reason. 40(1–2), 81–91 (2005)

    MathSciNet  MATH  Google Scholar 

  22. Yao, Y.Y.: Decision-theoretic rough set models. Lecture Notes Artif. Intell. 4481, 1–12 (2007)

    Google Scholar 

  23. Yao, Y.Y.: Probabilistic rough set approximations. Int. J. Approx. Reason. 49(2), 255–271 (2008)

    MATH  Google Scholar 

  24. Greco, S., Matarazzo, B., Slowinski, R.: Parameterized rough set model using rough membership and Bayesian confirmation measures. Int. J. Approx. Reason. 49(2), 285–300 (2008)

    MathSciNet  MATH  Google Scholar 

  25. Qian, Y.H., Liang, J.Y., Yao, Y.Y., Dang, C.Y.: MGRS: a multi-granulation rough set. Inf. Sci. 180(6), 949–970 (2010)

    MathSciNet  MATH  Google Scholar 

  26. Qian, Y.H., Zhang, H., Sang, Y.L., Liang, J.Y.: Multigranulation decision-theoretic rough sets. Int. J. Approx. Reason. 55(1), 225–237 (2014)

    MathSciNet  MATH  Google Scholar 

  27. Yao, Y.Y.: Three-way decision: an interpretation of rules in rough set theory. Lecture Notes Artif. Intell. 5589, 642–649 (2009)

    Google Scholar 

  28. Feng, T., Mi, J.S.: Variable precision multigranulation decision-theoretic fuzzy rough sets. Knowl. Based Syst. 91, 93–101 (2016)

    Google Scholar 

  29. Zhang, Q.H., Xie, Q., Wang, G.Y.: A novel three-way decision model with decision-theoretic rough sets using utility theory. Knowl. Based Syst. 159, 321–335 (2018)

    Google Scholar 

  30. Jiao, L., Yang, H.L., Li, S.G.: Three-way decision based on decision-theoretic rough sets with single-valued neutrosophic information. Int. J. Mach. Learn. Cybern. 11, 657–665 (2020)

    Google Scholar 

  31. Zhao, X.R., Hu, B.Q.: Three-way decisions with decision-theoretic rough sets in multiset-valued information tables. Inf. Sci. 507, 684–699 (2020)

    MathSciNet  MATH  Google Scholar 

  32. Zadeh, L.A.: Fuzzy sets. Inf. Control 8(3), 338–353 (1965)

    MATH  Google Scholar 

  33. Zadeh, L.A.: The concept of a linguistic variable and its application to approximate reasoning-I. Inf. Sci. 8(3), 199–249 (1975)

    MathSciNet  MATH  Google Scholar 

  34. Raj, D., Gupta, A., Garg, B., Tanna, K., Rhee, F.C.: Analysis of data generated from multidimensional type-1 and type-2 fuzzy membership functions. IEEE Trans Fuzzy Syst. 26(2), 681–693 (2018)

    Google Scholar 

  35. Pal, S.S., Kar, S.: A hybridized forecasting method based on weight adjustment of neural network using generalized type-2 fuzzy set. Int. J. Fuzzy Syst. 21(1), 308–320 (2019)

    Google Scholar 

  36. Wang, H.D., Yao, J.L., Yan, J., Dong, M.G.: An extended TOPSIS method based on gaussian interval type-2 fuzzy set. Int. J. Fuzzy Syst. 21(6), 1831–1843 (2019)

    Google Scholar 

  37. Karnik, N.N., Mendel, J.M., Liang, Q.L.: Type-2 fuzzy logic systems. IEEE Trans Fuzzy Syst. 7(6), 643–658 (2000)

    Google Scholar 

  38. Mendel, J.M., John, R.I.B.: Type-2 fuzzy sets made simple. IEEE Trans Fuzzy Syst. 10(2), 117–127 (2002)

    Google Scholar 

  39. Hu, B.Q., Wang, C.Y.: On type-2 fuzzy relations and interval-valued type-2 fuzzy sets. Fuzzy Sets Syst. 236(2), 1–32 (2014)

    MathSciNet  MATH  Google Scholar 

  40. Wang, C.Y.: Type-2 fuzzy rough sets based on extended t-norms. Inf. Sci. 305, 165–183 (2015)

    MathSciNet  MATH  Google Scholar 

  41. Lu, J., Li, D.Y., Zhai, Y.H., Li, H., Bai, H.X.: A model for type-2 fuzzy rough sets. Inf. Sci. 328(20), 359–377 (2016)

    MATH  Google Scholar 

  42. Singh, S., Garg, H.: Distance measures between type-2 intuitionistic fuzzy sets and their application to multicriteria decision-making process. Appl. Intell. 46(4), 88–799 (2017)

    Google Scholar 

  43. Li, J.W., John, R., Coupland, S., Kendall, G.: On Nie-Tan operator and type-reduction of interval type-2 fuzzy sets. IEEE Trans Fuzzy Syst. 26(2), 1036–1039 (2018)

    Google Scholar 

  44. Wu, D.R., Mendel, J.M.: Similarity measures for closed general type-2 fuzzy sets: overview, comparisons, and a geometric approach. Inf. Sci. 27(3), 515–526 (2019)

    Google Scholar 

  45. Feng, T., Mi, J.S., Zhang, S.P.: Belief functions on general intuitionistic fuzzy information systems. Inf. Sci. 271(1), 143–158 (2014)

    MathSciNet  MATH  Google Scholar 

  46. Lin, G.P., Liang, J.Y., Qian, Y.H., Li, J.J.: A fuzzy multigranulation decision-theoretic approach to multi-source fuzzy information systems. Knowl. Based Syst. 91, 102–113 (2016)

    Google Scholar 

  47. Li, Z.W., Liu, X.F., Zhang, G.Q., Xie, N.X., Wang, S.C.: A multi-granulation decision-theoretic rough set method for distributed \(fc\)-decision information systems: an application in medical diagnosis. Appl. Soft Comput. 56, 233–244 (2017)

    Google Scholar 

  48. Zhang, X.X., Chen, D.G., Tsang, E.C.C.: Generalized dominance-based rough set model for the dominance intuitionistic fuzzy information systems. Inf. Sci. 378, 1–25 (2017)

    MATH  Google Scholar 

  49. Zhang, G.Q., Li, Z.W., Wu, W.Z., Liu, X.F., Xie, N.X.: Information structures and uncertainty measures in a fully fuzzy information system. Int. J. Approx. Reason. 101, 119–149 (2018)

    MathSciNet  MATH  Google Scholar 

  50. Liu, X.F., Li, Z.W., Zhang, G.Q., Xie, N.X.: Measures of uncertainty for a distributed fully fuzzy information system. Int. J. Gen. Syst. 48(6), 625–655 (2019)

    MathSciNet  Google Scholar 

  51. Mendel, J.M.: Advances in type-2 fuzzy sets and systems. Inf. Sci. 177(1), 84–110 (2007)

    MathSciNet  MATH  Google Scholar 

  52. De Luca, A., Termini, S.: A definition of non-probabilistic entropy in the setting of fuzzy sets theory. Inf. Control 20, 301–312 (1972)

    MATH  Google Scholar 

  53. Sanchez, E.: Inverses of fuzzy relations: applications to possibility distributions and medical diagnosis. Fuzzy Sets Syst. 2, 75–86 (1979)

    MathSciNet  MATH  Google Scholar 

  54. John, R., Mendel, J., Carter, J.: The extended sup-star composition for type-2 fuzzy sets made simple. In: IEEE International Conference on Fuzzy Systems, pp. 7212–7216 (2006)

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Nos. 61976089, 61473259, 61070074, 60703038), the Natural Science Foundation of Hunan Province (2021JJ30451), and the Hunan Provincial Science & Technology Project Foundation (2018RS3065, 2018TP1018).

Author information

Authors and Affiliations

  1. College of Mathematics and Computer Science, Zhejiang Normal University, Jinhua, 321004, China

    Xiaofeng Liu

  2. Hunan Provincial Key Laboratory of Intelligent Computing and Language Information Processing, Hunan Normal University, Changsha, Hunan, 410081, China

    Xiaofeng Liu & Jianhua Dai

  3. College of Information Science and Engineering, Hunan Normal University, Changsha, Hunan, 410081, China

    Jianhua Dai

Authors
  1. Xiaofeng Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jianhua Dai
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jianhua Dai.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, X., Dai, J. A Fuzzy Decision-Theoretic Rough Set Approach for Type-2 Fuzzy Conditional Information Systems and Its Application in Decision-Making. Int. J. Fuzzy Syst. 24, 622–634 (2022). https://doi.org/10.1007/s40815-021-01167-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-021-01167-x

Keywords