Skip to main content

Advertisement

Springer Nature Link
Log in

Fuzzy Grey Model for Forecasting Non-homogeneous Exponential Sequence

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

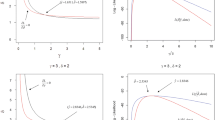
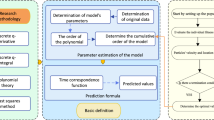
Getting accurate results when GM (1, 1) model is used for fitting and predicting approximate non-homogeneous exponential sequence, is a challenge. We sought to address this issue by combining Grey Theory and Credibility Theory, to develop a fuzzy GM (1, 1) model (FGM), which introduces the double exponential fuzzy numbers and its membership function. The expectation of fuzzy variables for replacing the non-homogeneous exponential sequence was calculated by Credibility Theory, i.e. the homogeneous process. The novel method yields unbiased results when used in fitting and predicting the tight non-homogeneous exponential sequence. Finally, we use an empirical case and a numerical sequence case to illustrate the effectiveness, feasibility, and optimization of the FGM (1, 1) model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Deng, J.L.: Control problems of grey systems. Syst. Control Lett. 1, 288–294 (1982)

    Article  MathSciNet  Google Scholar 

  2. Liu, S.F., Dang, Y.G., Fang, Z.G.: Grey System Theory and Its Application. Science Press, Beijing (2004)

    Google Scholar 

  3. Zeng, B., Meng, W., Tong, M.: A self-adaptive intelligence grey predictive model with alterable structure and its application. Eng. Appl. Artif. Intell. 50, 236–244 (2016)

    Article  Google Scholar 

  4. Mao, Y., Tu, Y., Yang, H.: A new method to eliminate negative frequency interference based on wavelet transformation and grey correlation theory. In: Intelligent Control and Automation. pp. 4356–4361 (2012).

  5. Liu, J.F., Liu, S.F., Fang, Z.G., et al.: New strengthening buffer operators based on adjustable intensity and their applications. J. Grey Syst. 26(3), 117–125 (2014)

    Google Scholar 

  6. Hsu, Y.T., Liu, M.C., Yeh, J., et al.: Forecasting the turning time of stock market based on Markov-fourier grey model. Exper Syst. Appl. 36, 8597–8603 (2009)

    Article  Google Scholar 

  7. Wang, R.Q., Wang, F.X., Ji, W.T.: Particle swarm optimization based gm(11) method on short-term electricity price forecasting with predicted error improvement. Appl. Mech. Mater. 40, 183–188 (2011)

    Article  Google Scholar 

  8. Peng, G., Wang, H., Song, X., et al.: Intelligent management of coal stockpiles using improved grey spontaneous combustion forecasting models. Energy 132, 269–279 (2017)

    Article  Google Scholar 

  9. Liu, E., Wang, Q., Ge, X., et al.: Dynamic discrete GM (1, 1) model and its application in the prediction of urbanization conflict events. Discrete Dyn. Nat. Soc. 1, 1–10 (2016)

    MathSciNet  MATH  Google Scholar 

  10. Dang, Y.C., Liu, S.F., Chen, K.: The GM models that x(n) be taken as initial value. Kvbernetes 33, 247–254 (2004)

    Article  Google Scholar 

  11. Wang, Y.H., Dang, Y.G., Li, Y.Q.: An approach to increase prediction precision of GM(1,1) model based on optimization of the initial condition. Expert Syst. Appl. 37, 5640–5644 (2010)

    Article  Google Scholar 

  12. Wang, Q.B., Jia, L.: Application of GM(1, 1) model based on residual error correction in athletic performance prediction. In: International Conference on Mechatronics, Materials, Chemistry and Computer Engineering. (2015).

  13. Zeng, B., Feng, L.S.: Direct modeling approach of dgm(1,1) with approximate non-homogeneous exponential sequence. Syst. Eng. Theory Pract. 31, 297–301 (2011)

    Google Scholar 

  14. Li, S., Miao, Y., Li, G., et al.: A novel varistructure grey forecasting model with speed adaptation and its application. Math. Comput. Simul. 172, 45–70 (2020)

    Article  MathSciNet  Google Scholar 

  15. Li, S., Ma, X., Yang, C.: A novel structure-adaptive intelligent grey forecasting model with full-order time power terms and its application. Comput. Ind. Eng. 120, 53–67 (2018)

    Article  Google Scholar 

  16. Zadeh, L.A.: Fuzzy sets. Inf. Control. 8, 338–353 (1965)

    Article  Google Scholar 

  17. Kaufmann, A., Bonaert, A.P.: Introduction to the theory of fuzzy subsets-vol. 1: fundamental theoretical elements. IEEE Trans. Syst. Man Cybern. 7, 495–496 (1977)

    Article  Google Scholar 

  18. Zadeh, L.A.: Fuzzy sets as a basis for a theory of possibility. Fuzzy Sets Syst. 1, 3–28 (1978)

    Article  MathSciNet  Google Scholar 

  19. Liu, B., Liu, Y.K.: Expected value of fuzzy variable and fuzzy expected value models. IEEE Trans. Fuzzy Syst. 10, 445–450 (2002)

    Article  Google Scholar 

  20. Liu, B.D.: Uncertainty Theory: An Introduction to its Axiomatic Foundations. Springer, Berlin (2004)

    Book  Google Scholar 

  21. Li X., Liu, B.D.: A sufficient and necessary condition for credibility measures. Int. J. Uncertainty Fuzziness Knowl. Based Syst. 14, 527–535 (2006)

  22. Xue, F., Tang, W., Zhao, R.: The expected value of a function of a fuzzy variable with a continuous membership function. Comput. Math. Appl. 55, 1215–1224 (2008)

    Article  MathSciNet  Google Scholar 

  23. Reddy, G.T., Reddy, M.P.K., Lakshmanna, K., et al.: Hybrid genetic algorithm and a fuzzy logic classifier for heart disease diagnosis. Evol. Intell. 13, 185–196 (2020)

    Article  Google Scholar 

  24. Asghar, M.Z., Subhan, F., Ahmad, H., et al.: Senti-eSystem: a sentiment-based eSystem-using hybridized fuzzy and deep neural network for measuring customer satisfaction. Softw. Pract. Exp. 51(3), 571–594 (2021)

    Article  Google Scholar 

  25. Wang, Z.X., Dang, Y.G., Liu, S.F.: An optimal gm(1,1) based on the discrete function with exponential law. Syst. Eng. Theory Pract. 2, 61–67 (2008)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the Guangdong Province Philosophy and Social Sciences “Thirteenth Five-Year” Planning Discipline Co-construction Fund (no. GD17XGL02).

Author information

Authors and Affiliations

  1. School of Computer Science, University of Electronic Science and Technology of China, Zhongshan Institute, Zhongshan, 528402, China

    Lei Cao

  2. School of Economics and Commerce, University of Electronic Science and Technology of China, Zhongshan Institute, Zhongshan, 528402, China

    Xiyu Cao

  3. School of Business Administration, Dongbei University of Finance and Economics, Dalian, 116025, China

    Qiangqiang Wang

  4. Lingnan College, Sun Yat-Sen University, Guangzhou, 510275, China

    Yiqiu Cao

Authors
  1. Lei Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiyu Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Qiangqiang Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Yiqiu Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Qiangqiang Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cao, L., Cao, X., Wang, Q. et al. Fuzzy Grey Model for Forecasting Non-homogeneous Exponential Sequence. Int. J. Fuzzy Syst. 24, 957–966 (2022). https://doi.org/10.1007/s40815-021-01179-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-021-01179-7

Keywords