Skip to main content

Advertisement

Springer Nature Link
Log in

Transitive Fuzzy Similarity Multigraph-Based Model for Alternative Clustering in Multi-criteria Group Decision-Making Problems

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

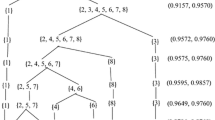
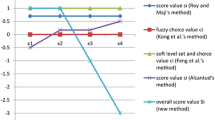
Graph node clustering methods, which aim to partition graph vertices into several disjoint groups of data with similar features, are usually fulfilled based on topological structural similarity of nodes, such as connectivity between vertices or neighborhood similarity of them. However, the attribute-based clustering is recently challenging to data clustering. The present paper contributes to considering a novel data clustering algorithm, called FBC-Cluster, based on fuzzy multigraphs in terms of both structural and attribute similarities. In the proposed algorithm, attribute similarity is achieved through m-polar fuzzy T-equivalences among alternatives (objects) and structural similarity is defined based on a new similarity measurement, called behavioral similarity index, using closed neighborhood in the attributed clusters. The output of the proposed clustering algorithm includes two main categories, namely certain and possible clusters, based on threshold level \(\beta\) given on the behavioral similarity index. A numerical example is discussed to demonstrate the performance of the designed clustering algorithm. The quality of resultant clusters is also evaluated through density and entropy functions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Agrawal, S., Patel, A.: SAG cluster: an unsupervised graph clustering based on collaborative similarity for community detection in complex networks. Physica A 563, 125459 (2021)

    Google Scholar 

  2. Akram, M., Shahzadi, G.: Certain characterization of m-polar fuzzy graphs by level graphs. Punjab Univ. J. Math. 49(1), 1–12 (2017)

    MathSciNet  MATH  Google Scholar 

  3. Baczynski, M., Jayaram, B.: Fuzzy Implications. Springer, Berlin (2008)

    MATH  Google Scholar 

  4. Bentkowska, U.: Aggregation of diverse types of fuzzy orders for decision making problems. Inf. Sci. 424, 317–336 (2018)

    MathSciNet  MATH  Google Scholar 

  5. Bentkowska, U., Król, A.: Preservation of fuzzy relation properties based on fuzzy conjunctions and disjunctions during aggregation process. Fuzzy Sets Syst. 291, 98–113 (2016)

    MathSciNet  MATH  Google Scholar 

  6. Bezdek, J.C.: Pattern Recognition with Fuzzy Objective Function Algorithms. Springer, Berlin (2013)

    MATH  Google Scholar 

  7. Bhattacharya, P.: Some remarks on fuzzy graphs. Pattern Recognit. Lett. 6(5), 297–302 (1987)

    MATH  Google Scholar 

  8. Boobalan, M.P., Lopez, D., Gao, X.Z.: Graph clustering using k-neighbourhood attribute structural similarity. Appl. Soft Comput. 47, 216–223 (2016)

    Google Scholar 

  9. Čaklović, L., Kurdija, A.S.: A universal voting system based on the potential method. Eur. J. Oper. Res. 259(2), 677–688 (2017)

    MathSciNet  MATH  Google Scholar 

  10. Chen, J., Li, S., Ma, S., Wang, X.: Polar fuzzy sets: an extension of bipolar fuzzy sets. Sci. World J. 2014 (2014)

  11. De Baets, B., Mesiar, R.: Metrics and t-equalities. J. Math. Anal. Appl. 267(2), 531–547 (2002)

    MathSciNet  MATH  Google Scholar 

  12. Dong, Y., Zhuang, Y., Chen, K., Tai, X.: A hierarchical clustering algorithm based on fuzzy graph connectedness. Fuzzy Sets Syst. 157(13), 1760–1774 (2006)

    MathSciNet  MATH  Google Scholar 

  13. Dudziak, U.: Preservation of t-norm and t-conorm based properties of fuzzy relations during aggregation process. In: 8th Conference of the European Society for Fuzzy Logic and Technology (EUSFLAT-13), pp. 416–423. Atlantis Press (2013)

  14. Fodor, J.C.: Strict preference relations based on weak t-norms. Fuzzy Sets Syst. 43(3), 327–336 (1991)

    MathSciNet  MATH  Google Scholar 

  15. Fodor, J.C., Roubens, M.: Fuzzy Preference Modelling and Multicriteria Decision Support, vol. 14. Springer, Berlin (1994)

    MATH  Google Scholar 

  16. Fodor, J.C., Ovchinnikov, S.: On aggregation of t-transitive fuzzy binary relations. Fuzzy Sets Syst. 72(2), 135–145 (1995)

    MathSciNet  MATH  Google Scholar 

  17. Fuchs, C., Spolaor, S., Nobile, M.S., Kaymak, U.: A graph theory approach to fuzzy rule base simplification. In: International Conference on Information Processing and Management of Uncertainty in Knowledge-Based Systems, pp. 387–401. Springer (2020)

  18. Gan, G.: Application of data clustering and machine learning in variable annuity valuation. Insur. Math. Econ. 53(3), 795–801 (2013)

    MathSciNet  MATH  Google Scholar 

  19. Ghorai, G., Pal, M.: Some properties of m-polar fuzzy graphs. Pac. Sci. Rev. A 18(1), 38–46 (2016)

    MATH  Google Scholar 

  20. Hammouda, K., Karray, F.: A Comparative Study of Data Clustering Techniques, vol. 1. University of Waterloo, Waterloo (2000)

    Google Scholar 

  21. Hashmi, M.R., Riaz, M., Smarandache, F.: m-Polar neutrosophic topology with applications to multi-criteria decision-making in medical diagnosis and clustering analysis. Int. J. Fuzzy Syst. 22(1), 273–292 (2020)

    Google Scholar 

  22. Huang, X., Lai, W.: Clustering graphs for visualization via node similarities. J. Vis. Lang. Comput. 17(3), 225–253 (2006)

    Google Scholar 

  23. Jain, A.K., Dubes, R.C.: Algorithms for Clustering Data. Prentice-Hall, Inc., Englewood Cliffs (1988)

    MATH  Google Scholar 

  24. Khameneh, A.Z., Kilicman, A.: m-Polar fuzzy soft graphs in group decision making: a combining method by aggregation functions. In: International Online Conference on Intelligent Decision Science, pp. 425–455. Springer (2020)

  25. Khameneh, A.Z., Kilicman, A.: Some construction methods of aggregation operators in decision-making problems: an overview. Symmetry 12(5), 694–714 (2020)

    Google Scholar 

  26. Li, Y., Pelusi, D., Deng, Y.: Generate two-dimensional belief function based on an improved similarity measure of trapezoidal fuzzy numbers. Comput. Appl. Math. 39(4), 1–20 (2020)

    MathSciNet  MATH  Google Scholar 

  27. Likas, A., Vlassis, N., Verbeek, J.J.: The global k-means clustering algorithm. Pattern Recognit. 36(2), 451–461 (2003)

    Google Scholar 

  28. Liu, X., Xu, Y., Herrera, F.: Consensus model for large-scale group decision making based on fuzzy preference relation with self-confidence: detecting and managing overconfidence behaviors. Inf. Fusion 52, 245–256 (2019)

    Google Scholar 

  29. Luqman, A., Akram, M., Koam, A.N.: An m-polar fuzzy hypergraph model of granular computing. Symmetry 11(4), 483 (2019)

    Google Scholar 

  30. Mathew, S., Sunitha, M.: Node connectivity and arc connectivity of a fuzzy graph. Inf. Sci. 180(4), 519–531 (2010)

    MathSciNet  MATH  Google Scholar 

  31. Mota, V.C., Damasceno, F.A., Leite, D.F.: Fuzzy clustering and fuzzy validity measures for knowledge discovery and decision making in agricultural engineering. Comput. Electron. Agric. 150, 118–124 (2018)

    Google Scholar 

  32. Nawaz, W., Khan, K.U., Lee, Y.K., Lee, S.: Intra graph clustering using collaborative similarity measure. Distrib. Parallel Databases 33(4), 583–603 (2015)

    Google Scholar 

  33. Raghavan, V.V., Yu, C.: A comparison of the stability characteristics of some graph theoretic clustering methods. IEEE Trans. Pattern Anal. Mach. Intell. 4, 393–402 (1981)

    MATH  Google Scholar 

  34. Rosenfeld, A.: Fuzzy graphs. In: Fuzzy Sets and Their Applications to Cognitive and Decision Processes, pp. 77–95. Elsevier, New York (1975)

  35. Schaeffer, S.E.: Graph clustering. Comput. Sci. Rev. 1(1), 27–64 (2007)

    MATH  Google Scholar 

  36. Sebastian, A., Mordeson, J.N., Mathew, S.: Generalized fuzzy graph connectivity parameters with application to human trafficking. Mathematics 8(3), 424 (2020)

    Google Scholar 

  37. Setnes, M., Babuska, R., Kaymak, U., van Nauta Lemke, H.R.: Similarity measures in fuzzy rule base simplification. IEEE Trans. Syst. Man Cybern. B 28(3), 376–386 (1998)

    Google Scholar 

  38. Singh, P.K.: m-Polar fuzzy graph representation of concept lattice. Eng. Appl. Artif. Intell. 67, 52–62 (2018)

    Google Scholar 

  39. Symeonidis, P., Tiakas, E., Manolopoulos, Y.: Transitive node similarity for link prediction in social networks with positive and negative links. In: Proceedings of the Fourth ACM Conference on Recommender Systems, pp. 183–190 (2010)

  40. Tanino, T.: Fuzzy preference orderings in group decision making. Fuzzy Sets Syst. 12(2), 117–131 (1984)

    MathSciNet  MATH  Google Scholar 

  41. Tiakas, E., Papadopoulos, A.N., Manolopoulos, Y.: Graph node clustering via transitive node similarity. In: 2010 14th Panhellenic Conference on Informatics, pp. 72–77. IEEE (2010)

  42. Wu, Y., Duan, H., Du, S.: Multiple fuzzy c-means clustering algorithm in medical diagnosis. Technol. Health Care 23(s2), S519–S527 (2015)

    Google Scholar 

  43. Wu, Z., Leahy, R.: An optimal graph theoretic approach to data clustering: theory and its application to image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 15(11), 1101–1113 (1993)

    Google Scholar 

  44. Xu, H., Yao, S., Li, Q., Ye, Z.: An improved k-means clustering algorithm. In: 2020 IEEE 5th International Symposium on Smart and Wireless Systems Within the Conferences on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS-SWS), pp. 1–5. IEEE (2020)

  45. Xue, Y., Deng, Y.: Refined expected value decision rules under orthopair fuzzy environment. Mathematics 8(3), 442 (2020)

    Google Scholar 

  46. Xue, Y., Deng, Y.: Decision making under measure-based granular uncertainty with intuitionistic fuzzy sets. Appl. Intell. (2021). https://doi.org/10.1007/s10489-021

    Article  Google Scholar 

  47. Yedla, M., Pathakota, S.R., Srinivasa, T.: Enhancing k-means clustering algorithm with improved initial center. Int. J. Comput Sci. Inf. Technol. 1(2), 121–125 (2010)

    Google Scholar 

  48. Zadeh, L.A.: Similarity relations and fuzzy orderings. Inf. Sci. 3(2), 177–200 (1971)

    MathSciNet  MATH  Google Scholar 

  49. Zahedi Khameneh, A., Kilicman, A.: m-Polar generalization of fuzzy t-ordering relations: an approach to group decision making. Symmetry 13(1), 51 (2021)

    Google Scholar 

  50. Zhou, Y., Cheng, H., Yu, J.X.: Graph clustering based on structural/attribute similarities. Proc. VLDB Endow. 2(1), 718–729 (2009)

    Google Scholar 

Download references

Acknowledgements

This research was supported by the Fundamental Research Grant Schemes, Ref. No.: FRGS/1/2019/STG06/UPM/02/6, awarded by the Malaysia Ministry of Higher Education (MOHE).

Author information

Authors and Affiliations

  1. Institute for Mathematical Research, Universiti Putra Malaysia, UPM, 43400, Serdang, Selangor, Malaysia

    Azadeh Zahedi Khameneh, Adem Kilicman & Fadzilah Md Ali

  2. Department of Mathematics, Faculty of Science, Universiti Putra Malaysia, UPM, 43400, Serdang, Selangor, Malaysia

    Adem Kilicman & Fadzilah Md Ali

Authors
  1. Azadeh Zahedi Khameneh
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Adem Kilicman
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Fadzilah Md Ali
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Azadeh Zahedi Khameneh.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khameneh, A.Z., Kilicman, A. & Ali, F.M. Transitive Fuzzy Similarity Multigraph-Based Model for Alternative Clustering in Multi-criteria Group Decision-Making Problems. Int. J. Fuzzy Syst. 24, 2569–2590 (2022). https://doi.org/10.1007/s40815-021-01213-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-021-01213-8

Keywords