Skip to main content
Springer Nature Link
Log in

A Hybrid PSO–GWO Fuzzy Logic Controller with a New Fuzzy Tuner

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

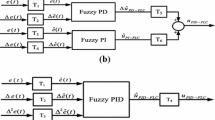
A hybrid PSO–GWO PID-type fuzzy logic controller (FLC) with a new online fuzzy tuner is proposed in this study to control a second-order system with varying parameters. Initially, the output scaling factors and the universe of discourse of membership functions for the PID-type FLC are optimized employing a hybrid particle swarm optimization (PSO) and grey wolf optimization (GWO) technique. The superiority of the hybrid PSO–GWO has been demonstrated by comparing with other methods, namely PSO, GWO, and hybrid CS (cuckoo search)–GWO. Additionally, a new online fuzzy tuner structure is proposed by tuning a single output scaling factor to overcome the major disadvantages of the previous approach using the relative rate observer and fuzzy parameter regulator (RRO–FPR). Simulation results show that all the given optimal PID-type FLCs with the proposed new fuzzy tuner produce a better system performance and exhibit a shorter settling time/rise time than the RRO–FPR approach. The proposed optimal PID-type FLC with a fuzzy tuner, which is optimized by the hybrid PSO–GWO method, proves to be superior to others given in this study by exhibiting the shortest settling time/rise time and the lowest overshoot in a practical application to the speed control of a nonlinear DC motor system. Therefore, utilization of the proposed, improved controller to nonlinear systems in dealing with dead-zone and unexpected disturbance is highly feasible.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Santos, M., Dexter, A.: Control of a cryogenic process using a fuzzy PID scheduler. Control Eng. Pract. 10(10), 1147–1152 (2002)

    Article  Google Scholar 

  2. Siddique, N.: Intelligent Control: A Hybrid Approach Based on Fuzzy Logic, Neural Networks and Genetic Algorithms. Springer, New York (2014)

    Book  Google Scholar 

  3. Huang, X., Shi, L.: Simulation on a fuzzy-PID position controller of the CNC servo system. In: 2006 International Conference on Intelligent Systems Design and Applications. IEEE 1, pp. 305–309 (2006)

  4. Kha, N.B., Ahn, K.K.: Position control of shape memory alloy actuators by using self tuning fuzzy PID controller. In: 2006 Conference on Industrial Electronics and Applications. IEEE, pp. 1–5 (2006)

  5. Lee, C.-D., Chuang, C.-W., Kao, C.-C.: Apply fuzzy PID rule to PDA based control of position control of slider crank mechanisms. In: 2004 Conference on Cybernetics and Intelligent Systems. IEEE 1, pp. 508–513 (2004)

  6. Reznik, L., Ghanayem, O., Bourmistrov, A.: PID plus fuzzy controller structures as a design base for industrial applications. Eng. Appl. Artif. Intell. 13(4), 419–430 (2000)

    Article  Google Scholar 

  7. Tamilarasi, D., Sivakumaran, T.S.: Fuzzy PI control of symmetrical and asymmetrical multilevel current source inverter. Int. J. Fuzzy Syst. 20(2), 426–443 (2018)

    Article  Google Scholar 

  8. He, S.-Z., Tan, S., Xu, F.-L., Wang, P.-Z.: Fuzzy self-tuning of PID controllers. Fuzzy Sets Syst. 56(1), 37–46 (1993)

    Article  MathSciNet  Google Scholar 

  9. Mizumoto, M.: Realization of PID controls by fuzzy control methods. Fuzzy Sets Syst. 70, 171–182 (1995)

    Article  MathSciNet  Google Scholar 

  10. Zhao, Z.-Y., Tomizuka, M., Isaka, S.: Fuzzy gain scheduling of PID controllers. IEEE Trans. Syst. Man Cybern. Syst. 23(5), 1392–1398 (1993)

    Article  Google Scholar 

  11. Zhao, T., Chen, Y., Dian, S., Gou, R., Li, S.: General type-2 fuzzy gain scheduling PID controller with application to power-line inspection robots. Int. J. Fuzzy Syst. 22(1), 587–596 (2020)

    Article  Google Scholar 

  12. Zheng, Z., Wang, N., Sun, Z.: Fuzzy PI compound control of PWM rectifiers with applications to marine vehicle electric propulsion system. Int. J. Fuzzy Syst. 20(2), 587–596 (2018)

    Article  MathSciNet  Google Scholar 

  13. Chang, C.-W., Tao, C.-W., Chuang, C.-C.: Design of a DSP-based PD-like fuzzy controller for buck DC–DC converters. Int. J. Fuzzy Syst. 18(6), 971–979 (2016)

    Article  MathSciNet  Google Scholar 

  14. Hu, B., Mann, G.K., Gosine, R.G.: New methodology for analytical and optimal design of fuzzy PID controllers. IEEE Trans. Fuzzy Syst. 7(5), 521–539 (1999)

    Article  Google Scholar 

  15. Xu, J.-X., Hang, C.-C., Liu, C.: Parallel structure and tuning of a fuzzy PID controller. Automatica 36(5), 673–684 (2000)

    Article  MathSciNet  Google Scholar 

  16. Galichet, S., Foulloy, L.: Fuzzy controllers: synthesis and equivalences. IEEE Trans. Fuzzy Syst. 3(2), 140–148 (1995)

    Article  Google Scholar 

  17. Mudi, R.K., Pal, N.R.: A robust self-tuning scheme for PI-and PD-type fuzzy controllers. IEEE Trans. Fuzzy Syst. 7(1), 2–16 (1999)

    Article  Google Scholar 

  18. Trabia, M.B., McCarthy, W.E.: Design of fuzzy logic controllers for optimal performance. J. Intell. Fuzzy Syst. 6(4), 459–470 (1998)

    Google Scholar 

  19. Simon, D.: Sum normal optimization of fuzzy membership functions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 10(4), 363–384 (2002)

    Article  MathSciNet  Google Scholar 

  20. Bouallegue, S., Haggege, J., Ayadi, M., Benrejeb, M.: PID-type fuzzy logic controller tuning based on particle swarm optimization. Eng. Appl. Artif. Intell. 25(3), 484–493 (2012)

    Article  Google Scholar 

  21. Noshadi, A., Shi, J., Lee, W.S., Shi, P., Kalam, A.: Optimal PID-type fuzzy logic controller for a multi-input multi-output active magnetic bearing system. Neural Comput. Appl. 27(7), 2031–2046 (2016)

    Article  Google Scholar 

  22. Sahu, R.K., Panda, S., Sekhar, G.C.: A novel hybrid PSO-PS optimized fuzzy PI controller for AGC in multi area interconnected power systems. Int. J. Electr. Power Energy Syst. 64, 880–893 (2015)

    Article  Google Scholar 

  23. Premkumar, K., Manikandan, B.: Bat algorithm optimized fuzzy PD based speed controller for brushless direct current motor. Eng. Sci. Technol. Int. J. 19(2), 818–840 (2016)

    Google Scholar 

  24. Normey-Rico, J.E., Camacho, E.F.: Control of Dead-Time Processes. Springer, New York (2007)

    MATH  Google Scholar 

  25. Chung, H.-Y., Chen, B.-C., Lin, J.-J.: A PI-type fuzzy controller with self-tuning scaling factors. Fuzzy Sets Syst. 93(1), 23–28 (1998)

    Article  Google Scholar 

  26. Guzelkaya, M., Eksin, I., Yesil, E.: Self-tuning of PID-type fuzzy logic controller coefficients via relative rate observer. Eng. Appl. Artif. Intell. 16(3), 227–236 (2003)

    Article  Google Scholar 

  27. Karasakal, O., Guzelkaya, M., Eksin, I., Yesil, E., Kumbasar, T.: Online tuning of fuzzy PID controllers via rule weighing based on normalized acceleration. Eng. Appl. Artif. Intell. 26(1), 184–197 (2013)

    Article  Google Scholar 

  28. Woo, Z.-W., Chung, H.-Y., Lin, J.-J.: A PID type fuzzy controller with self-tuning scaling factors. Fuzzy Sets Syst. 115(2), 321–326 (2000)

    Article  Google Scholar 

  29. Golob, M.: Decomposed fuzzy proportional–integral–derivative controllers. Appl. Soft Comput. 1(3), 201–214 (2001)

    Article  Google Scholar 

  30. Guzelkaya, M., Gurleyen, F.: A new methodology for designing a fuzzy logic controller and PI, PD blending mechanism. J. Intell. Fuzzy Syst. 11, 85–98 (2001)

    Google Scholar 

  31. Qiao, W.Z., Mizumoto, M.: PID type fuzzy controller and parameters adaptive method. Fuzzy Sets Syst. 78(1), 23–35 (1996)

    Article  MathSciNet  Google Scholar 

  32. Tsai, M.T., Tung, P.C., Chen, K.Y.: Experimental evaluations of proportional–integral–derivative type fuzzy controllers with parameter adaptive methods for an active magnetic bearing system. Expert Syst. 28(1), 5–18 (2011)

    Article  Google Scholar 

  33. Takagi, T., Sugeno, M.: Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. Syst. 1, 116–132 (1985)

    Article  Google Scholar 

  34. Mamdani, E.H., Assilian, S.: An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 7(1), 1–13 (1975)

    Article  Google Scholar 

  35. Eberhart, R., Kenedy, J.: Particle swarm optimization. In: 1995 Proceedings of the IEEE International Conference on Neural Networks. IEEE 4, pp. 1942–1948 (1995)

  36. Mirjalili, S., Mirjalili, S.M., Lewis, A.: Grey wolf optimizer. Adv. Eng. Softw. 69, 46–61 (2014)

    Article  Google Scholar 

  37. Yang, X.-S., Deb, S.: Cuckoo search: Recent advances and applications. Neural Comput. Appl. 24(1), 169–174 (2014)

    Article  Google Scholar 

  38. Long, W., Cai, S., Jiao, J., Xu, M., Wu, T.: A new hybrid algorithm based on grey wolf optimizer and cuckoo search for parameter extraction of solar photovoltaic models. Energy Conv. Manag. 203, 1–9 (2020)

    Article  Google Scholar 

  39. Singh, N., Singh, S.: Hybrid algorithm of particle swarm optimization and grey wolf optimizer for improving convergence performance. J. Appl. Math. 2017, 1–15 (2017)

    Article  MathSciNet  Google Scholar 

  40. Hekimoglu, B.: Optimal tuning of fractional order PID controller for DC motor speed control via chaotic atom search optimization algorithm. IEEE Access 7, 38100–38114 (2019)

    Article  Google Scholar 

  41. Tung, P.-C., Chen, S.-C.: Experimental and analytical studies of the sinusoidal dither signal in a DC motor system. Dynam. Control 3(1), 53–69 (1993)

    Article  MathSciNet  Google Scholar 

  42. Guechi, E.-H., Lauber, J., Dambrine, M., Klancar, G., Blazic, S.: PDC control design for non-holonomic wheeled mobile robots with delayed outputs. J. Intell. Robot. Syst. 60(3), 395–414 (2010)

    Article  Google Scholar 

  43. Zhuang, G., Su, S.-F., Xia, J., Sun, W.: HMM-based asynchronous H∞ filtering for fuzzy singular Markovian switching systems with retarded time-varying delays. IEEE Trans. Cybern. 51(3), 1189–1203 (2020)

    Article  Google Scholar 

  44. Zhuang, G., Sun, W., Su, S.-F., Xia, J.: Asynchronous feedback control for delayed fuzzy degenerate jump systems under observer-based event-driven characteristic. IEEE Trans. Fuzzy Syst. (2020). https://doi.org/10.1109/TFUZZ.2020.3027336

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the Ministry of Science and Technology (Taiwan) under Contract Nos. MOST 109-2218-E-008-003 and MOST 108-2218-E-008-019.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, National Central University, Jhong-Li District, Tao-Yuan City, 32001, Taiwan

    Dinh-Tu Nguyen, Jeng-Rong Ho, Pi-Cheng Tung & Chih-Kuang Lin

Authors
  1. Dinh-Tu Nguyen
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jeng-Rong Ho
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Pi-Cheng Tung
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Chih-Kuang Lin
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Chih-Kuang Lin.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguyen, DT., Ho, JR., Tung, PC. et al. A Hybrid PSO–GWO Fuzzy Logic Controller with a New Fuzzy Tuner. Int. J. Fuzzy Syst. 24, 1586–1604 (2022). https://doi.org/10.1007/s40815-021-01215-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-021-01215-6

Keywords