Skip to main content

Advertisement

Springer Nature Link
Log in

Soft Bond Game Options Valuation in Discrete Time Using a Fuzzy-Stochastic Approach

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

Bond game options are complex financial instruments that include the aspects of the risk (stochastic uncertainty) of a term structure of interest rates, option (flexibility) and interactivity (game). Forecasting uncertainty also comprises the vagueness (fuzzy uncertainty), often neglected. The fuzzy-stochastic models encompass both features. The paper objective is to develop and apply the fuzzy-stochastic soft bond game option model in discrete time. This model is based on normal fuzzy sets of the T-number type, the decomposition principle and \(\varepsilon{\text{-}}cuts\). The forward induction arbitrage-free method for the Ho–Lee calibration of interest rates, the binomial model and the two-person zero-sum games are used. An application example of the fuzzy-stochastic soft bond game option model from the buyer perspective based on the power triangle numbers for three variants of fuzziness is developed and computed. Inclusion of vagueness allows reflecting better valuation conditions and getting a more complex valuation picture. The developed model can adequately reflect valuation conditions and considers all aspects of the complex valuation problem of the bond game options, besides risk, flexibility, interactivity and vagueness.

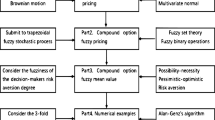
Graphical Abstract

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

Not applicable.

Code Availability

Not applicable.

References

  1. Kifer, Y.: Game options. Financ. Stoch. 4, 443–463 (2000). https://doi.org/10.1007/PL00013527

    Article  MathSciNet  MATH  Google Scholar 

  2. Ben-Ameur, H., Breton, M., Karoui, L., L’Ecuyer, P.: A dynamic programming approach for pricing options embedded in bonds. J. Econ. Dyn. Control 31, 2212–2233 (2007). https://doi.org/10.1016/j.jedc.2006.06.007

    Article  MathSciNet  MATH  Google Scholar 

  3. Dolinsky, Y.: Hedging of game options under model uncertainty in discrete time. Electron. Commun. Probab. (2014). https://doi.org/10.1214/ECP.v19-2714

    Article  MathSciNet  MATH  Google Scholar 

  4. Dolinsky, Y., Iron, Y., Kifer, Y.: Perfect and partial hedging for swing game options in discrete time. Math. Financ. 21, 447–474 (2011). https://doi.org/10.1111/j.1467-9965.2010.00440.x

    Article  MathSciNet  MATH  Google Scholar 

  5. Dolinsky, Y., Kifer, Y.: Hedging with risk for game options in discrete time. Stochastics 79, 169–195 (2007). https://doi.org/10.1080/17442500601097784

    Article  MathSciNet  MATH  Google Scholar 

  6. Kallsen, J., Kuhn, C.: Pricing derivatives of American and game type in incomplete markets. Financ. Stoch. 8, 261–284 (2004). https://doi.org/10.1007/s00780-003-0110-7

    Article  MathSciNet  MATH  Google Scholar 

  7. Ohtsubo, Y.: Optimal stopping in sequential games with or without a constraint of always terminating. Math. Oper Res. 11, 591–607 (1986). https://doi.org/10.1287/moor.11.4.591

    Article  MathSciNet  MATH  Google Scholar 

  8. Sebehela, T.: Game options. Ann. Financ. Econ. 12(3), 18 (2017). https://doi.org/10.1142/S2010495217500154

    Article  Google Scholar 

  9. Beveridge, C., Joshi, M.: Monte Carlo bounds for game options including convertible bonds. Manag. Sci. 57(5), 960–974 (2011). https://doi.org/10.2139/ssrn.1577593

    Article  MATH  Google Scholar 

  10. Chen, N., Dai, M., Wan, X.: A non-zero-sum game approach to convertible bonds: tax benefits, bankruptcy costs and early/late calls. Math. Financ. 23(1), 57–93 (2013). https://doi.org/10.1111/j.1467-9965.2011.00488.x

    Article  MATH  Google Scholar 

  11. Kwok, Y.K.: Game option models of convertible bonds: determinants of call policies. J. Financ. Eng. 1(4), 19 (2014). https://doi.org/10.1142/S2345768614500299

    Article  MathSciNet  Google Scholar 

  12. Ochiai, N., Ohnishi, M.: Valuation of game option bonds under the generalised Ho-Lee model: a stochastic game approach. J. Math. Financ. 5, 412–422 (2015). https://doi.org/10.4236/jmf.2015.54035

    Article  Google Scholar 

  13. Sirbu, M., Shreve, S.E.: A two-person game for pricing convertible bonds. SIAM J. Control Optim. 45(4), 1508–1539 (2006). https://doi.org/10.1137/050630222

    Article  MathSciNet  MATH  Google Scholar 

  14. Carlsson, C., Fuller, R.: A fuzzy approach to real option valuation. Fuzzy Sets Syst. 139, 297–312 (2003). https://doi.org/10.1016/s0165-0114(02)00591-2

    Article  MathSciNet  MATH  Google Scholar 

  15. Chrysafis, K.A., Papadopoulos, B.K.: On theoretical pricing of options with fuzzy estimators. J. Comput. Appl. Math. 223(2), 552–566 (2009). https://doi.org/10.1016/j.cam.2007.12.006

    Article  MathSciNet  MATH  Google Scholar 

  16. Driouchi, T., Trigeorgis, L., Gao, Y.: Choquet-based European option pricing with stochastic (and fixed) strikes. OR Spectrum 37(3), 787–802 (2015). https://doi.org/10.1007/s00291-014-0378-3

    Article  MathSciNet  MATH  Google Scholar 

  17. Guerra, M. L., Sorini, L., Stefanini, L.: Parametrised fuzzy numbers for option pricing. In: IEEE International Conference on Fuzzy Systems, London, vol. 1–4, pp. 727–732 (2007) https://doi.org/10.1109/fuzzy.2007.4295456

  18. Liyan, H., Wenli, C.: The generalisation of λ-fuzzy measures with application to the fuzzy option. In: Wang, L. et al. (eds.) Proceedings: Fuzzy Systems and Knowledge Discovery, LNAI, vol. 4223, pp. 762–765. Springer, Berlin (2006). https://doi.org/10.1007/11881599_93

  19. Simonelli, M.R.: Fuzziness in valuing financial instruments by certainty equivalents. Eur. J. Oper. Res. 135(2), 296–302 (2001). https://doi.org/10.1016/s0377-2217(01)00041-8

    Article  MathSciNet  MATH  Google Scholar 

  20. Thiagarajaha, K., Appadoob, S.S., Thavaneswaranc, A.: Option valuation model with adaptive fuzzy numbers. Comput. Math. Appl. 53, 831–841 (2007). https://doi.org/10.1016/j.camwa.2007.01.011

    Article  MathSciNet  Google Scholar 

  21. Wu, H.C.: European option pricing under fuzzy environments. Int. J. Intell. Syst. 20, 89–102 (2005). https://doi.org/10.1002/int.20055

    Article  MATH  Google Scholar 

  22. Wu, H.C.: Using fuzzy sets theory and Black-Scholes formula to generate pricing boundaries of European options. Appl. Math. Comput. 185(1), 136–146 (2007). https://doi.org/10.1016/j.amc.2006.07.015

    Article  MathSciNet  MATH  Google Scholar 

  23. Yoshida, Y.: The valuation of European options in uncertain environment. Eur. J. Oper. Res. 145, 221–229 (2003). https://doi.org/10.1016/s0377-2217(02)00209-6

    Article  MathSciNet  MATH  Google Scholar 

  24. Zhang, J., Du, H., Tang, W.: Pricing R&D option with combining randomness and fuzziness. In: Computational intelligence, PT 2, Proceedings Book Series: Lecture Notes in Artificial Intelligence, vol. 4114, pp. 798–808 (2006). https://doi.org/10.1007/978-3-540-37275-2_100

  25. Zmeškal, Z.: Application of the fuzzy-stochastic methodology to appraising the firm value as a European calls option. Eur. J. Oper. Res. 135(2), 303–310 (2001). https://doi.org/10.1016/s0377-2217(01)00042-x

    Article  MathSciNet  MATH  Google Scholar 

  26. Cheng, F.-L., Tzeng, G.-H., Wang, S.-Y.: A fuzzy set approach for generalised CRR model: an empirical analysis of S&P 500 Index options. Rev. Quant. Financ. Acc. 25, 255–275 (2005). https://doi.org/10.1007/s11156-005-4767-1

    Article  Google Scholar 

  27. Muzzioli, S., De Baets, B.: Fuzzy approaches to option price modeling. IEEE Trans. Fuzzy Syst. 25(2), 392–401 (2017). https://doi.org/10.1109/tfuzz.2016.2574906

    Article  Google Scholar 

  28. Muzzioli, S., Reynaerts, H.: The solution of fuzzy linear systems by non-linear programming: a financial application. Eur. J. Oper. Res. 177, 1218–1231 (2007). https://doi.org/10.1016/j.ejor.2005.10.055

    Article  MATH  Google Scholar 

  29. Muzzioli, S., Reynaerts, H.: American option pricing with imprecise risk-neutral probabilities. Int. J. Approx. Reason. 49(1), 140–147 (2008). https://doi.org/10.1016/j.ijar.2007.06.011

    Article  MATH  Google Scholar 

  30. Nowak, P., Romaniuk, M.: Fuzzy approach to option pricing in a Levy process setting. Int. J. Appl. Math. Comput. Sci. 23(3), 613–622 (2013). https://doi.org/10.2478/amcs-2013-0046

    Article  MathSciNet  MATH  Google Scholar 

  31. Yoshida, Y.: A discrete-time model of American put option in an uncertain environment. Eur. J. Oper. Res. 151, 153–166 (2002). https://doi.org/10.1016/s0377-2217(02)00591-x

    Article  MathSciNet  MATH  Google Scholar 

  32. Yoshida, Y., Yasuda, M., Nakagami, J., Kurano, M.: A discrete-time American put option model with fuzziness of stock prices. Fuzzy Optim. Decis. Mak. 4(3), 191–207 (2005). https://doi.org/10.1007/s10700-005-1889-9

    Article  MathSciNet  MATH  Google Scholar 

  33. Zhang, W.G., Li, Z., Liu, Y.J., et al.: Pricing European option under fuzzy mixed fractional Brownian motion model with jumps. Comput. Econ. 58, 483–515 (2021). https://doi.org/10.1007/s10614-020-10043-z

    Article  Google Scholar 

  34. Zmeškal, Z.: Generalised soft binomial American real option pricing model (fuzzy–stochastic approach). Eur. J. Oper. Res. 207(2), 1096–1103 (2010). https://doi.org/10.1016/j.ejor.2010.05.045

    Article  MathSciNet  MATH  Google Scholar 

  35. Zmeškal, Z., Dluhošová, D., Gurný, P., Kresta, A.: Generalised soft multi-mode real options model (fuzzy - stochastic approach). Expert Syst. Appl. (2022). https://doi.org/10.1016/j.eswa.2021.116388

    Article  Google Scholar 

  36. Yoshida, Y.: A zero-sum stopping game in a continuous-time dynamic fuzzy system. Math. Comput. Model. 34(5–6), 603–614 (2001). https://doi.org/10.1016/S0895-7177(01)00086-3

    Article  MathSciNet  MATH  Google Scholar 

  37. Ho Thomas, S.Y., Lee, S.-B.: Term structure movement and pricing interest rate contingent claims. J. Financ. 41(5), 1011–1029 (1986). https://doi.org/10.1007/978-1-4614-5360-4_25

    Article  Google Scholar 

  38. Jamshidian, F.: An exact bond option formula. J. Financ. 44, 205–209 (1989). https://doi.org/10.1111/j.1540-6261.1989.tb02413.x

    Article  Google Scholar 

  39. Jamshidian, F.: Forward induction and construction of yield curve diffusion models. J. Fixed Income 1, 62–74 (1991). https://doi.org/10.3905/jfi.1991.692348

    Article  Google Scholar 

  40. Jamshidian, F.: Bond futures and option evaluation in the quadratic interest rate model. Appl. Math. Financ. 3, 93–115 (1996). https://doi.org/10.1080/13504869600000005

    Article  MATH  Google Scholar 

  41. Clewlow, L., Strickland, Ch.: Implementing Derivatives Models. Wiley, New York (1998)

    Google Scholar 

  42. Dubois, D., Prade, H.: Fuzzy Sets and Systems. Academic Press, New York (1980)

    MATH  Google Scholar 

  43. Inuiguchi, M., Ramík, J.: Possibilistic linear programming: a brief review of fuzzy mathematical programming and comparison with stochastic programming in portfolio selection problem. Fuzzy Sets Syst. 111, 3–28 (2000). https://doi.org/10.1016/s0165-0114(98)00449-7

    Article  MathSciNet  MATH  Google Scholar 

  44. Kacprzyk, J., Fedrizzi, M.: Combining Fuzzy Imprecision with Probabilistic Uncertainty in Decision-Making. Springer, Heidelberg (1988). https://doi.org/10.1007/978-3-642-46644-1

    Book  MATH  Google Scholar 

  45. Kruse, R., Meyer, D.: Descriptive Statistics with Vague Data. Series B: Mathematical and Statistical Methods. Reidel, Dodrecht (1987). https://doi.org/10.1007/978-94-009-3943-1_8

    Book  Google Scholar 

  46. Luhandjula, M.K.: Fuzzy stochastic linear programming: survey and future research directions. Eur. J. Oper. Res. 174(3), 1353–1367 (2006). https://doi.org/10.1016/j.ejor.2005.07.019

    Article  MathSciNet  MATH  Google Scholar 

  47. Luhandjula, M.K.: Fuzziness and randomness in an optimisation framework. Fuzzy Sets Syst. 77, 291–297 (1996). https://doi.org/10.1016/0165-0114(95)00043-7

    Article  MathSciNet  MATH  Google Scholar 

  48. Sakawa, M., Kato, K., Nishizaki, I.: An interactive fuzzy satisfying method for multiobjective stochastic linear programming problems through an expectation model. Eur. J. Oper. Res. 145(3), 665–672 (2003). https://doi.org/10.1016/s0377-2217(02)00150-9

    Article  MATH  Google Scholar 

  49. Van Hop, N.: Fuzzy stochastic goal programming problems. Eur. J. Oper. Res. 176(1), 77–86 (2007). https://doi.org/10.1016/j.ejor.2005.09.023

    Article  MathSciNet  MATH  Google Scholar 

  50. Viertl, R.: Statistical Methods for Non-Precise Data. CRC Press, Boca Raton (1996). https://doi.org/10.1007/978-3-642-04898-2_546

    Book  MATH  Google Scholar 

  51. Wang, G.Y., Qiao, Z.: Linear programming with fuzzy-random variable coefficients. Fuzzy Sets Syst. 57, 295–311 (1993). https://doi.org/10.1016/0165-0114(93)90025-d

    Article  MathSciNet  MATH  Google Scholar 

  52. Zadeh, L.A.: Fuzzy sets. Inf. Control 8(3), 338–353 (1965). https://doi.org/10.1016/S0019-9958(65)90241-X

    Article  MATH  Google Scholar 

  53. Ramík, J., Rommelfanger, H.: Fuzzy mathematical programming based on some new inequality relations. Fuzzy Sets Syst. 81, 77–87 (1996). https://doi.org/10.1016/0165-0114(95)00241-3

    Article  MathSciNet  MATH  Google Scholar 

  54. Zadeh, L.A.: Concept of a linguistic variable and its application to approximate reasoning. Inf. Sci. 9(1), 43–80 (1975). https://doi.org/10.1016/0020-0255(75)90017-1

    Article  MathSciNet  MATH  Google Scholar 

  55. Zadeh, L.A.: Similarity relation and fuzzy ordering. Inf. Sci. (1971). https://doi.org/10.1016/S0020-0255(71)80005-1

    Article  MathSciNet  Google Scholar 

  56. Puri, M.L., Ralescu, D.A.: Fuzzy random variables. J. Math. Anal. Appl. 114, 409–422 (1986). https://doi.org/10.1515/9783110917833.452

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The paper is supported by the Grant Agency of the VSB-Technical University Ostrava SP2022/58, SP2021/57. This support is gratefully acknowledged.

Funding

The research was funded by the VSB-Technical University Ostrava.

Author information

Authors and Affiliations

  1. Department of Finance, Faculty of Economics, VSB - Technical University of Ostrava, Sokolska 33, 701 21, Ostrava 1, Czech Republic

    Zdeněk Zmeškal, Dana Dluhošová, Petr Gurný & Haochen Guo

Authors
  1. Zdeněk Zmeškal
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Dana Dluhošová
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Petr Gurný
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Haochen Guo
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

All authors contributed to the paper conception, methodology and formal analysis and investigation. The first draft of the manuscript was written by ZZ, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript. Conceptualisation: ZZ, DD, PG and HG; Methodology: ZZ, DD, PG and HG; Software: ZZ; Writing—Original Draft: ZZ; Writing—Review & Editing: DD, PG, HG; Funding acquisition: DD; Formal analysis and investigation: ZZ, DD, PG, HG.

Corresponding author

Correspondence to Zdeněk Zmeškal.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zmeškal, Z., Dluhošová, D., Gurný, P. et al. Soft Bond Game Options Valuation in Discrete Time Using a Fuzzy-Stochastic Approach. Int. J. Fuzzy Syst. 24, 2215–2228 (2022). https://doi.org/10.1007/s40815-022-01258-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-022-01258-3

Keywords