Consensus Reaching Process for Group Decision Making with Distributed Preference Relations Under Fuzzy Uncertainty

Abstract

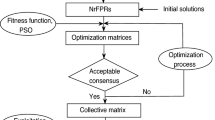
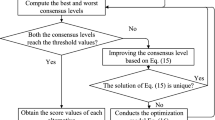
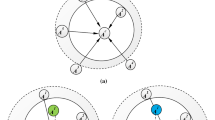
In group decision-making (GDM) problems, the elicitation of preferences from decision makers (DMs) and consensus reaching process are two critical issues to be resolved. Many kinds of preference relations have been proposed in the recent two decades. In this paper, we propose a novel pairwise comparison structure called fuzzy-uncertainty-based distributed preference relation (FUDPR), which could not only indicate the intensity of preferred, non-preferred, indifferent and uncertain information of one alternative against another simultaneously, but also has the ability to represent local ignorance expressed by DMs. The FUDPR introduces the set of consecutive evaluation grades into the distributed preference relation (DPR) where only discrete single evaluation grades and global ignorance can be modeled in the preference relation. The missing values in FUDPR are estimated by the defined score function. Two kinds of consensus reaching process (CRP) are then proposed, namely soft and hard consensus mechanism, respectively, which are suitable for different decision-making situations. Both of them consider the individual dissimilarity, trust relations and self-confidence in the designed feedback mechanism. Comparative analysis is performed between the proposed method and other state-of-the-art pairwise comparison GDM models. An illustrative example of life cycle sustainability assessment (LCSA) is proposed to demonstrate the rationality and effectiveness of the proposed method in supporting real-world GDM problems.

Appendices

Appendix

Proof of Theorem 2

Given a FUDPR such that ${r}_{ij}^{t}=\left\{\left({H}_{mn},{\beta }_{ij}^{t}\left({H}_{mn}\right)\right). m,n=\mathrm{1,2},\ldots ,N;m\le n\right\}$. The following two situations may occur.

(1) When $m<n$, ${\beta }_{ij}^{t}\left({H}_{mn}\right)$ signifies the belief degree of local ignorance, so it can be assigned to any grade between ${H}_{m}$ and ${H}_{n}$. Suppose that it’s assigned to ${H}_{\xi }(m\le \xi \le n,\xi \in \{\mathrm{1,2},\ldots ,N\})$, the score of ${H}_{mn}$ will satisfy the following condition:

$$\mathrm{s}({H}_{m})\le \mathrm{s}({H}_{\xi })\le \mathrm{s}({H}_{n})$$

Then

$${{s}_{ij}^{t}}^{-}\le \sum_{m=1}^{N}\sum_{n=1}^{N}{\beta }_{ij}^{t}\left({H}_{mn}\right)\cdot \mathrm{s}({H}_{\xi })\le {{s}_{ij}^{t}}^{+}$$

(2) When $m=n$, we have

$$\mathrm{s}\left({H}_{m}\right)=\mathrm{s}\left({H}_{mn}\right)=\mathrm{s}({H}_{n})$$

Then

$${{s}_{ij}^{t}}^{-}=\sum_{m=1}^{M}{\beta }_{ij}^{t}\left({H}_{mm}\right)\cdot \mathrm{s}({H}_{mm})={{s}_{ij}^{t}}^{+}$$

Combining the above two situations, the following conclusions can be drawn:

$${{s}_{ij}^{t}}^{-}\le \sum_{m=1}^{N}\sum_{n=m+1}^{N}{\beta }_{ij}^{t}\left({H}_{mn}\right)\cdot \mathrm{s}({H}_{\xi })+\sum_{m=1}^{M}{\beta }_{ij}^{t}\left({H}_{mm}\right)\cdot \mathrm{s}({H}_{mm})\le {{s}_{ij}^{t}}^{+}$$

Proof of Theorem 3

According to Definition 5, it can be concluded that

$${{s}_{ij}^{t}}^{-}+{{s}_{ji}^{t}}^{+}=\sum_{m=1}^{N}\sum_{n=m}^{N}{\beta }_{ij}^{t}\left({H}_{mn}\right)\cdot s({H}_{m})+\sum_{m=1}^{N}\sum_{n=m}^{N}{\beta }_{ji}^{t}\left({H}_{mn}\right)\cdot s({H}_{n})$$

From Property 2, we have

$${\beta }_{ij}^{t}({H}_{mn})={\beta }_{ji}^{t}({H}_{\left(N-n+1\right)\left(N-m+1\right)})$$

And Remark 1 indicates that

$$s\left({H}_{m}\right)=s\left({H}_{mm}\right)=-s\left({H}_{\left(N-m+1\right)\left(N-m+1\right)}\right)$$

As for ${H}_{mn}$, when $m=n$, ${H}_{mn}$ represents a single grade ${H}_{m}$ or ${H}_{n}$, so it can be inferred that

$$s\left({H}_{m}\right)+s\left({H}_{N-m+1}\right)=0$$

Then we can conclude that

$${\beta }_{ij}^{t}\left({H}_{mn}\right)\cdot s\left({H}_{m}\right)=-{\beta }_{ji}^{t}({H}_{\left(N-n+1\right)\left(N-m+1\right)})\cdot s\left({H}_{N-m+1}\right)$$

For any ${\beta }_{ij}^{t}({H}_{mn}) \cdot s({H}_{m})$ in ${r}_{ij}^{t}$, there’s always $-{\beta }_{ji}^{t}({H}_{\left(N-n+1\right)\left(N-m+1\right)})\cdot s\left({H}_{N-m+1}\right)$ in ${r}_{ji}^{t}$ that corresponds to it, so we have

$$\sum_{m=1}^{N}\sum_{n=m}^{N}\left({\beta }_{ij}^{t}\left({H}_{mn}\right)\cdot \mathrm{s}\left({H}_{m}\right)+{\beta }_{ji}^{t}({H}_{\left(N-n+1\right)\left(N-m+1\right)})\cdot s\left({H}_{N-m+1}\right)\right)=0$$

Then

$$\sum_{m=1}^{N}\sum_{n=m}^{N}{\beta }_{ji}^{t}({H}_{\left(N-n+1\right)\left(N-m+1\right)})\cdot s\left({H}_{N-m+1}\right)=\sum_{m=1}^{N}\sum_{n=m}^{N}{\beta }_{ji}^{t}\left({H}_{mn}\right)\cdot s\left({H}_{n}\right)$$

So the following conclusion can be drawn:

$$\sum_{m=1}^{N}\sum_{n=m}^{N}{\beta }_{ij}^{t}\left({H}_{mn}\right)\cdot s({H}_{m})+\sum_{m=1}^{N}\sum_{n=m}^{N}{\beta }_{ji}^{t}\left({H}_{mn}\right)\cdot s({H}_{n})=0$$

Thus, we have

$${{s}_{ij}^{t}}^{+}+{{s}_{ji}^{t}}^{-}=0$$

Similarly, we can prove that ${{s}_{ij}^{t}}^{-}+{{s}_{ji}^{t}}^{+}=0$.

Proof of Property 4

Given the preference relations of ${DM}_{t}$ and ${DM}_{{t}^{^{\prime}}}$ such that ${r}_{i(i+1)}^{t}=\left\{{H}_{11},1\right\}$ and ${r}_{i(i+1)}^{{t}^{^{\prime}}}=\left\{{H}_{NN},1\right\}$ respectively. The distributed dissimilarity between the two DMs is:

$${DD}_{i(i+1)}^{t{t}^{^{\prime}}}=\left\{\left({H}_{11},1\right),\left({H}_{NN},1\right)\right\}$$

According to Definition 9, we have:

$${AD}_{i(i+1)}^{t{t}^{^{\prime}}}=\frac{1\times 1\times \left|1-(-1)\right|}{1-(-1)}=1$$

Similarly, when ${r}_{i(i+1)}^{t}=\left\{{H}_{NN},1\right\}$ and ${r}_{i(i+1)}^{{t}^{^{\prime}}}=\left\{{H}_{11},1\right\}$, we also have ${AD}_{i(i+1)}^{t{t}^{^{\prime}}}=1$.