Skip to main content

Advertisement

Springer Nature Link
Log in

An Application of Fully Intuitionistic Fuzzy Multi-objective Linear Fractional Programming Problem in E-education System

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

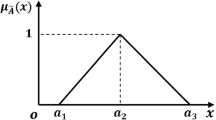
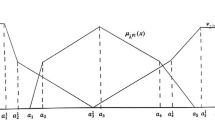
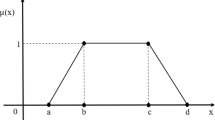
Abstract

This article addresses a special class of non-linear programming problems, viz., linear fractional programming problems having multiple objectives. In solving the real-life linear fractional optimization problems, the ambiguity and hesitation in the decision are inherent and ever-present, therefore, it is perfectly viable to formulate and solve these optimization models using the intuitionistic fuzzy environment. The purpose of this study is to propose a simple and computationally efficient approach to obtain the solution of multiple objective linear fractional programming problems having all the decision variables and parameters expressed in terms of triangular intuitionistic fuzzy numbers. The proposed solution algorithm is primarily based on the goal programming approach, fuzzy-based linearization technique, and a membership function strategy. The original linear fractional programming problem is first converted to its equivalent deterministic/crisp multi-objective linear fractional optimization problem using the weighted goal programming methodology along with the linear membership technique to resolve the intuitionistic fuzzy constraints into the crisp one. Finally, the variable transformation technique for the under- and over-deviational variables of the goal programming model is employed to linearize all the fractions involved in the problem so as to convert the original problem to an equivalent linear optimization problem. Further, this linear programming problem can be solved using any available commercial packages. Moreover, a numerical illustration is provided to demonstrate the steps of the proposed technique followed by the analysis and solution of an E-education set-up problem. The discussion and comparisons of the practical case establish the relevancy and usefulness of the proposed model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Abbreviations

LFP:

Linear fractional programming

MOLFP:

Multi-objective linear fractional programming

DM:

Decision-maker

IF:

Intuitionistic fuzzy

IF-LFP:

Intuitionistic fuzzy linear fractional programming

IF-MO-LFP:

Intuitionistic fuzzy multi-objective linear fractional programming

IFN:

Intuitionistic fuzzy number

TIFN:

Triangular intuitionistic fuzzy number

s. t.:

Subject to

ELC:

E-learning centre

References

  1. Stancu-Minasian, I.M.: Fractional Programming: Theory, Methods and Applications. Kluwer Academic Publishers, Dordrecht (1997)

    Book  MATH  Google Scholar 

  2. Zhu, H., Huang, G.H.: SLFP: a stochastic linear fractional programming approach for sustainable waste management. Waste Manag. 31, 2612–2619 (2011)

    Article  Google Scholar 

  3. Bajalinov, E.B.: Linear-Fractional programming: Theory, Methods, Applications and Software. Kluwer Academic Publishers, Boston (2003)

    Book  MATH  Google Scholar 

  4. Charnes, A., Cooper, W.W.: Programming with linear fractional functionals. Naval Res. Logist. Q. 9, 181–186 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bitran, G.R., Novaes, A.G.: Linear programming with a fractional objective function. Oper. Res. 21, 22–29 (1973)

    Article  MathSciNet  MATH  Google Scholar 

  6. Tantawy, S.: An iterative method for solving linear fractional programming (LFP) problem with sensitivity analysis. Math. Comput. Appl. 13, 147–151 (2008)

    MathSciNet  MATH  Google Scholar 

  7. Tantawy, S.F.: A new concept of duality for linear fractional programming problems. Int. J. Eng. Innov. Technol. 3, 147–149 (2014)

    Google Scholar 

  8. Wu, Z., Gao, Q., Jiang, B., Karimi, H.R.: Solving the production transportation problem via a deterministic annealing neural network method. Appl. Math. Comput. 411, 126518 (2021)

    MathSciNet  MATH  Google Scholar 

  9. Wu, Z., Karimi, H.R., Dang, C.: An approximation algorithm for graph partitioning via deterministic annealing neural network. Neural Netw. 117, 191–200 (2019)

    Article  MATH  Google Scholar 

  10. Luhandjula, M.K.: Fuzzy approaches for multiple objective linear fractional optimization. Fuzzy Sets Syst. 13, 11–23 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  11. Dutta, D., Rao, J.R., Tiwari, R.N.: Sensitivity analysis in fractional programming-the tolerance approach. Int. J. Syst. Sci. 23, 823–832 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  12. Chakraborty, M., Gupta, S.: Fuzzy mathematical programming for multi objective linear fractional programming problem. Fuzzy Sets Syst. 125, 335–342 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  13. Pal, B.B., Moitra, B.N., Maulik, U.: A goal programming procedure for fuzzy multiobjective linear fractional programming problem. Fuzzy Sets Syst. 139, 395–405 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  14. Guzel, N., Sivri, M.: Taylor series solution of multi objective linear fractional programming problem. Trakya Univ. J. Sci. 6, 91–98 (2005)

    Google Scholar 

  15. Chang, C.-T.: Fuzzy linearization strategy for multiple objective linear fractional programming with binary utility functions. Comput. Ind. Eng. 112, 437–446 (2017)

    Article  Google Scholar 

  16. Bellman, R.E., Zadeh, L.A.: Decision making in a fuzzy environment. Manage. Sci. 17, 141–164 (1970)

    Article  MathSciNet  MATH  Google Scholar 

  17. Abo-Sinna, M.A., Baky, I.A.: Fuzzy goal programming procedure to bilevel multiobjective linear fractional programming problems. Int. J. Math. Math. Sci. (2010). https://doi.org/10.1155/2010/148975

    Article  MathSciNet  MATH  Google Scholar 

  18. Li, D., Chen, S.: A fuzzy programming approach to fuzzy linear fractional programming with fuzzy coefficients. J. Fuzzy Math. 4, 829–833 (1996)

    MathSciNet  MATH  Google Scholar 

  19. Pop, B., Stancu-Minasian, I.M.: A method of solving fully fuzzified linear fractional programming problems. J. Appl. Math. Comput. 27, 227–242 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. Veeramani, C., Sumathi, M.: Solving the linear fractional programming problem in a fuzzy environment: numerical approach. Appl. Math. Model. 40, 6148–6164 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  21. Ebrahimnejad, A., Ghomi, S.J., Mirhosseini-Alizamini, S.M.: A revisit of numerical approach for solving linear fractional programming problem in a fuzzy environment. Appl. Math. Model. 57, 459–473 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  22. Arya, R., Singh, P., Bhati, D.: A fuzzy based branch and bound approach for multi-objective linear fractional (MOLF) optimization problems. J. Comput. Sci. 24, 54–64 (2018)

    Article  MathSciNet  Google Scholar 

  23. Arya, R., Singh, P., Kumari, S., Obaidat, M.S.: An approach for solving fully fuzzy multi-objective linear fractional optimization problems. Soft. Comput. 24, 9105–9119 (2020)

    Article  MATH  Google Scholar 

  24. Luo, Q., Nguyen, A.-T., Fleming, J., Zhang, H.: Unknown input observer based approach for distributed tube-based model predictive control of heterogeneous vehicle platoons. IEEE Trans. Veh. Technol. 70(4), 2930–2944 (2021)

    Article  Google Scholar 

  25. Ju, Z., Zhang, H., Tan, Y.: Distributed Stochastic Model Predictive Control for Heterogeneous Vehicle Platoons Subject to Modeling Uncertainties. IEEE Intell. Transp. Syst. Mag. 14(2), 25–40 (2021)

    Article  Google Scholar 

  26. Singh, S.K., Yadav, S.P.: Scalarizing fuzzy multi-objective linear fractional programming with application. Comput. Appl. Math. 41(3), 1–26 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  27. Stanojević, B.: Extension principle-based solution approach to full fuzzy multi-objective linear fractional programming. Soft Comput. 12, 1–8 (2022)

    Google Scholar 

  28. Borza, M., Rambely, A.S.: An approach based on α-cuts and max-min technique to linear fractional programming with fuzzy coefficients. Iran. J. Fuzzy Syst. 19(1), 153–168 (2022)

    MathSciNet  MATH  Google Scholar 

  29. Stanojević, B., Stanojević, M.: Empirical α,β-acceptable optimal values to full fuzzy linear fractional programming problems. Procedia Comput. Sci. 199, 34–39 (2022)

    Article  Google Scholar 

  30. Jayalakshmi, M.: Solving intuitionistic fuzzy linear fractional programming problem. Int. J. Sci. Res. Eng. Stud. 2, 29–32 (2015)

    Google Scholar 

  31. Singh, S.K., Yadav, S.P.: Fuzzy programming approach for solving intuitionistic fuzzy linear fractional programming problem. Int. J. Fuzzy Syst. 18, 263–269 (2016)

    Article  MathSciNet  Google Scholar 

  32. Amer, A.H.: An interactive intuitionistic fuzzy non-linear fractional programming problem. Int. J. Appl. Eng. Res. 13, 8116–8125 (2018)

    Google Scholar 

  33. Bharati, S.K.: Trapezoidal intuitionistic fuzzy fractional transportation problem. In: Bansal, J., Das, K., Nagar, A., Deep, K., Ojha, A. (eds.) Soft Computing for Problem Solving: Advances in Intelligent Systems and Computing, pp. 833–842. Springer, Singapore (2019)

    Chapter  Google Scholar 

  34. Ali, I., Gupta, S., Ahmed, A.: Multi-objective linear fractional inventory problem under intuitionistic fuzzy environment. Int. J. Syst. Assurance Eng. Manag. 10, 173–189 (2019)

    Article  Google Scholar 

  35. El Sayed, M.A., Abo-Sinna, M.A.: A novel approach for fully intuitionistic fuzzy multi-objective fractional transportation problem. Alex. Eng. J. 60, 1447–1463 (2021)

    Article  Google Scholar 

  36. Sahoo, D., Tripathy, A.K., Pati, J.K.: Study on multi-objective linear fractional programming problem involving pentagonal intuitionistic fuzzy number. Results Control Optim. 6, 100091 (2022)

    Article  Google Scholar 

  37. Batamiz, A., Allahdadi, M., Hladík, M.: Obtaining efficient solutions of interval multi-objective linear programming problems. Int. J. Fuzzy Syst. 22(3), 873–890 (2020)

    Article  Google Scholar 

  38. Rizk-Allah, R.M., Abo-Sinna, M.A., Hassanien, A.E.: Intuitionistic fuzzy sets and dynamic programming for multi-objective non-linear programming problems. Int. J. Fuzzy Syst. 23(2), 334–352 (2021)

    Article  Google Scholar 

  39. Khalil, S., Kousar, S., Freen, G., Imran, M.: Multi-objective interval-valued neutrosophic optimization with application. Int. J. Fuzzy Syst. (2021). https://doi.org/10.1007/s40815-021-01192-w

    Article  Google Scholar 

  40. Cheng, P., He, S., Stojanovic, V., Luan, X., Liu, F.: Fuzzy fault detection for Markov jump systems with partly accessible hidden information: an event-triggered approach. IEEE Trans. Cybern. (2021). https://doi.org/10.1109/TCYB.2021.3050209

    Article  Google Scholar 

  41. Ren, C., He, S., Luan, X., Liu, F., Karimi, H.R.: Finite-time L2-gain asynchronous control for continuous-time positive hidden Markov jump systems via T–S fuzzy model approach. IEEE Trans. Cybern. 51(1), 77–87 (2020)

    Article  Google Scholar 

  42. Mohamed, R.H.: The relationship between goal programming and fuzzy programming. Fuzzy Sets Syst. 89, 215–222 (1997)

    Article  MathSciNet  Google Scholar 

  43. Charnes, A., Cooper, W.W.: Management Models and Industrial Applications of Linear Programming. Wiley, New York (1961)

    MATH  Google Scholar 

  44. Ijiri, Y.: Management Goals and Accounting for Control. North Holland, Amsterdam (1965)

    Google Scholar 

  45. Lee, S.M.: Goal Programming for Decision Analysis. Auerbach Publisher, Philadelphia (1972)

    Google Scholar 

Download references

Acknowledgements

The authors are deeply thankful to the Editor and the anonymous referees for their fruitful comments which helped us to improve the overall quality of the manuscript. Moreover, the first author is grateful to the Ministry of Human Resource Development, India, for financial support, to carry out this research work. The second author would like to acknowledge the Uttarakhand State Council for Science and Technology, Dehradun, India to provide financial support to carry out this work under the Project No. UCS &T/R7D-19/20-21/19222/1.

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Roorkee, Roorkee, 247 667, India

    Manisha Malik & S. K. Gupta

Authors
  1. Manisha Malik
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. S. K. Gupta
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to S. K. Gupta.

Ethics declarations

Competing Interests

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Malik, M., Gupta, S.K. An Application of Fully Intuitionistic Fuzzy Multi-objective Linear Fractional Programming Problem in E-education System. Int. J. Fuzzy Syst. 24, 3544–3563 (2022). https://doi.org/10.1007/s40815-022-01348-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-022-01348-2

Keywords