Skip to main content
Springer Nature Link
Log in

TOPSIS Method Based on Hesitant Factor and Priority Weighted Operator in Pythagorean Fuzzy Environment

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

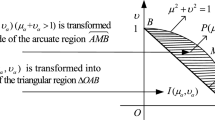
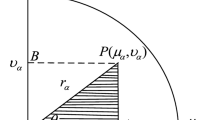
The main innovation of this paper is to transform Pythagorean fuzzy numbers (PFNs) into the analytic representation of centroid coordinates and hesitation factors through the transformation, and then the unified ranking method, distance measure and similarity with respect to PFNs are proposed using geometric method. These concepts can not only overcome some defects of existing methods, but also be applied to multi-attribute group decision-making problems. In this paper, the centroid coordinate representation of PFN is first introduced with regard to the hesitation region, when considering the degree of nonzero hesitation, the hesitation factor is proposed by comparing with the smallest element (0,1), and a new ranking method for PFNs is given by calculating the hesitation factor in the Pythagorean fuzzy number environment. Secondly, the distance measure and degree of similarity are put forward through the hesitation factor and centroid coordinates, and the Pythagorean fuzzy priority weighted average (PFPWA) operator is given by improving the priority weight parameter. Besides, the basic properties of PFPWA operator are discussed. Finally, the positive (negative) hesitation factor solutions, bidirectional projections and degrees of closeness for group comprehensive evaluation matrix are obtained, and a new TOPSIS method for dealing with multi-attribute decision-making problems is given under the Pythagorean fuzzy environment. The given example shows that the proposed method not only expands the scope of application and reduces the loss of some fuzzy information, but also eliminates the impact of abnormal data on the aggregation results by considering the priority of experts.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Atanassov, K.: Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20(1), 87–96 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  2. Chen, S.M., Tan, J.M.: Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 67(2), 163–172 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  3. Hong, D.H., Choi, C.H.: Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 114(1), 103–113 (2000)

    Article  MATH  Google Scholar 

  4. Yager, R.R.: Pythagorean fuzzy subsets. In: Proceeding Joint IFSA World Congress and NAFIPS Annual Meeting, Edmonton, Canada, pp. 57–61 (2013)

  5. Yager, R.R., Abbasov, A.M.: Pythagorean membership grades, complex numbers and decision Making. Int. J. Intell. Syst. 28, 436–452 (2013)

    Article  Google Scholar 

  6. Yager, R.R.: Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. Publ. IEEE Neural Netw. Council 22(4), 958–965 (2014)

    Google Scholar 

  7. Zhang, X.L., Xu, Z.S.: Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int. J. Intell. Syst. 29(12), 1061–1078 (2014)

    Article  MathSciNet  Google Scholar 

  8. Zhang, X.L.: A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making. Int. J. Intell. Syst. 31(6), 593–611 (2016)

    Article  MathSciNet  Google Scholar 

  9. Peng, X.D., Yang, Y.: Some results for Pythagorean fuzzy sets. Int. J. Intell. Syst. 30(11), 1133–1160 (2015)

    Article  MathSciNet  Google Scholar 

  10. Gou, X., Xu, Z.S., Ren, P.: The properties of continuous Pythagorean fuzzy information. Int. J. Intell. Syst. 31(5), 401–424 (2016)

    Article  Google Scholar 

  11. Garg, H.: A novel correlation coefficients between Pythagorean fuzzy sets and its applications to decision-making processes. Int. J. Intell. Syst. 31(12), 1234–1252 (2016)

    Article  Google Scholar 

  12. Garg, H.: A novel accuracy function under interval-valued Pythagorean fuzzy environment for solving multicriteria decision making problem. J. Intell. Fuzzy Syst. 31(1), 529–540 (2016)

    Article  MATH  Google Scholar 

  13. Garg, H.: A novel improved accuracy function for interval valued Pythagorean fuzzy sets and its applications in decision making process. Int. J. Intell. Syst. 31(12), 1247–1260 (2017)

    Article  Google Scholar 

  14. Garg, H.: A new improved score function of an interval-valued Pythagorean fuzzy set based TOPSIS method. Int. J. Uncertain Quantif. 7(5), 463–474 (2017)

    Article  Google Scholar 

  15. Akram, M., Garg, H., Zahid, K.: Extensions of ELECTRE-I and TOPSIS methods for group decision-making under complex Pythagorean fuzzy environment. Iran. J. Fuzzy Syst. 17(5), 147–164 (2020)

    Google Scholar 

  16. Ren, P.J., Xu, Z.S., Gou, X.J.: Pythagorean fuzzy TODIM approach to multi-criteria decision making. Appl. Soft Comput. 42, 246–259 (2016)

    Article  Google Scholar 

  17. Rahman, K., Abdullah, S., Ahmad, R.: Pythagorean fuzzy Einstein geometric operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 33, 635–647 (2016)

    Article  Google Scholar 

  18. Peng, X.D., Ma, X.L.: Pythagorean fuzzy multi-criteria decision making method based on CODAS with new score function. J. Intell. Fuzzy Syst. 38, 3307–3318 (2020)

    Article  Google Scholar 

  19. Xu, Z.S.: Dependent uncertain ordered weighted aggregation operators. Inf. Fusion 9(3), 310–316 (2008)

    Article  Google Scholar 

  20. Yager, R.R.: Prioritized OWA aggregation. Fuzzy Optim. Decis. Mak. 8(3), 245–262 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  21. Wei, G.W., Zhao, X.F.: Some dependent aggregation operators with 2-tuple linguistic systems with application to multiple attribute group decision making. Expert Syst. Appl. 39(5), 5881–5886 (2012)

    Article  Google Scholar 

  22. Verma, R., Sharma, B.D.: Intuitionistic Fuzzy Einstein prioritized weighted average operators and their application to multiple attribute group decision making. Appl. Math. Inf. Sci. 9, 3095–3107 (2015)

    Google Scholar 

  23. Peng, D.H., Yang, Y.: Pythagorean fuzzy prioritized aggregation operators and its application in decision making. Granul. Comput. 55(18), 218–222 (2019)

    Google Scholar 

  24. Hwang, C.L., Yoon, K.: Multiple Attribute Decision Making: Methods and Application. Springer, Berlin (1981)

    Book  MATH  Google Scholar 

  25. Walczak, D., Rutkowska, A.: Project rankings for participatory budget based on the fuzzy TOPSIS method. Eur. J. Oper. Res. 260(2), 706–714 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  26. Yazdi, M.: Risk assessment based on novel intuitionistic fuzzy-hybrid-modified TOPSIS approach. Saf. Sci. 110(12), 438–448 (2017)

    Google Scholar 

  27. Shih, H., Shyur, H., Lee, E.: An extension of TOPSIS for group decision making. Math. Comput. Modell. 45(7–8), 801–813 (2007)

    Article  MATH  Google Scholar 

  28. Ye, Y., Li, Y.: Group multi-attribute decision model to partner selection in the formation of virtual enterprise under incomplete information. Expert Syst. Appl. 36, 9350–9357 (2009)

    Article  Google Scholar 

  29. Chen, C.T.: Extensions of the TOPSIS for group decision making under fuzzy environment. Fuzzy Sets Syst. 114, 1–9 (2000)

    Article  MATH  Google Scholar 

  30. Tan, C.Q., Zhang, Q.: Fuzzy multiple attribute decision making based on interval-valued intuitionistic fuzzy sets. In: Proceeding of the 2006 IEEE international conference on systems, vol. 2, pp. 1404–1407 (2006)

  31. Tan, C.Q.: A multi-criteria interval-valued intuitionistic fuzzy group decision making with Choquet integral-based TOPSIS. Expert Syst. Appl. 38(4), 3023–3033 (2011)

    Article  Google Scholar 

  32. Liang, D.C., Xu, Z.S., Liu, D., et al.: Method for three-way decisions using ideal TOPSIS solutions at Pythagorean fuzzy information. Inf. Sci. 435, 282–295 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  33. Sun, G., Guan, X., Yi, X., et al.: An innovative TOPSIS approach based on hesitant fuzzy correlation coefficient and its applications. Appl. Soft Comput. 68, 249–267 (2018)

    Article  Google Scholar 

  34. Wang, G.J., Tao, Y.J., Li, Y.H.: TOPSIS evaluation system of logistics transportation based on an ordered representation of the polygonal fuzzy set. Int. J. Fuzzy Syst. 22(5), 1565–1581 (2020)

    Article  Google Scholar 

  35. Wang, G.J., Duan, Y.: TOPSIS approach for multi-attribute decision making problems based on \(n\)-intuitionistic polygonal fuzzy sets description. Comput. Ind. Eng. 124(10), 573–581 (2018)

    Article  Google Scholar 

  36. Duan, Y., Wang, G.J.: A FCM clustering algorithm based on polygonal fuzzy numbers to describe multiple attribute index information. Syst. Eng. Theory Pract. 36(12), 3220–3228 (2016)

    Google Scholar 

  37. Li, X.P., Tao, Y.J., Li, Y.H.: Decision making method for evaluating logistics companies based on the ordered representation of the polygonal fuzziness. J. Intell. Fuzzy Syst. 9(3), 3151–3166 (2020)

    Article  Google Scholar 

  38. Li, X.P., Li, Y.H., Tao, Y.J.: Representation and aggregation of multi-source information of modern smart cities based on the intuitionistic polygonal fuzzy set. Int. J. Fuzzy Syst. 23(4), 967–983 (2021)

    Article  Google Scholar 

  39. Sun, G., Li, X.P., Chen, D.G.: Ranking defects and solving countermeasures for Pythagorean fuzzy sets with hesitant degree. Int. J. Mach. Learn. Cybern. 13(5), 1265–1281 (2022)

    Article  Google Scholar 

  40. Sun, G., Wang, M.X., Li, X.P.: Centroid coordinate ranking of Pythagorean fuzzy numbers and its application in group decision making. Cogn. Comput. 14(2), 602–623 (2022)

    Article  Google Scholar 

Download references

Funding

This work has been supported by National Natural Science Foundation of China (Grant Nos. 61463019, 61374009) and Natural Science Foundation of Hunan Province (Grant No. 2019JJ40062).

Author information

Authors and Affiliations

  1. School of Science, Hunan Institute of Technology, Hengyang, 421002, Hunan, China

    Gang Sun

  2. Junior High School of Zhumadian, Zhumadian, 463003, Henan, China

    Jing Luo

  3. School of Mathematical Science, Tianjin Normal University, Tianjin, 300387, China

    Guijun Wang

Authors
  1. Gang Sun
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jing Luo
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Guijun Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Guijun Wang.

Ethics declarations

Conflict of Interest

The authors declare that they have no conflict of interest.

Ethical Approval

This article does not contain any studies with human participants or animals performed by any of the authors.

Informed Consent

Informed consent was obtained from all individual participants included in the study.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, G., Luo, J. & Wang, G. TOPSIS Method Based on Hesitant Factor and Priority Weighted Operator in Pythagorean Fuzzy Environment. Int. J. Fuzzy Syst. 25, 831–850 (2023). https://doi.org/10.1007/s40815-022-01406-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-022-01406-9

Keywords