Skip to main content

Advertisement

Springer Nature Link
Log in

Historical Data-Driven Composite Learning Adaptive Fuzzy Control of Fractional-Order Nonlinear Systems

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

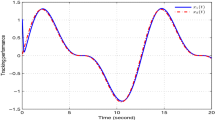
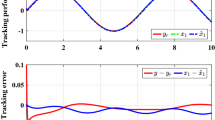
Different from traditional adaptive fuzzy control, this paper introduces a composite learning adaptive backstepping fuzzy control method using historical data which mainly focuses on improving the approximation accuracy of fuzzy logic systems for functional uncertainties of fractional-order nonlinear systems. A command filter is employed to settle the “explosion of complexity” issue that resulted from differentiating virtual controllers repeatedly in each backstepping step, and a compensation signal is defined to reduce the impact of filtered errors on control performance. In addition, a modified prediction error is defined to construct a composite parameter adaptation law, where the compensated error dynamic system equation is integrated in a moving time interval such that all historical data are integrated into a regressor vector to calculate the prediction error. The method introduced can not only ensure the boundedness of all signals in the closed-loop system based on the fractional Lyapunov stability criterion, but also realize the precise approximation to functional uncertainties. Finally, two numerical simulation examples are presented to demonstrate the superior effect of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Data Availability

Data sharing is not applicable to this article since there are no associated data.

References

  1. Magin, R.L.: “Fractional calculus in bioengineering: A tool to model complex dynamics.” In: Proceedings of the 13th International Carpathian Control Conference (ICCC), pp. 464–469, IEEE (2012)

  2. Kumar, D., Baleanu, D.: Fractional calculus and its applications in physics. Frontiers in Physics 7, 81 (2019)

    Article  Google Scholar 

  3. Ming, H., Wang, J., Fečkan, M.: The application of fractional calculus in chinese economic growth models. Mathematics 7(8), 665 (2019)

    Article  Google Scholar 

  4. Kumar, D., Singh, J.: Fractional Calculus in Medical and Health Science. CRC Press, Boca Raton (2020)

    Book  MATH  Google Scholar 

  5. Li, Y., Chen, Y., Podlubny, I.: Mittag-leffler stability of fractional order nonlinear dynamic systems. Automatica 45(8), 1965–1969 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  6. Fei, J., Wang, H., Fang, Y.: Novel neural network fractional-order sliding-mode control with application to active power filter. IEEE Transactions on Systems, Man, and Cybernetics: Systems 52(6), 3508–3518 (2022)

    Article  Google Scholar 

  7. You, X., Dian, S., Liu, K., Guo, B., Xiang, G., Zhu, Y.: Command filter-based adaptive fuzzy finite-time tracking control for uncertain fractional-order nonlinear systems. IEEE Transactions on Fuzzy Systems, 1–14 (2022). https://doi.org/10.1109/TFUZZ.2022.3185453

  8. Wang, L., Dong, J.: Reset event-triggered adaptive fuzzy consensus for nonlinear fractional-order multiagent systems with actuator faults. IEEE Transactions on Cybernetics, 1–12 (2022). https://doi.org/10.1109/TCYB.2022.3163528

  9. Doostdar, F., Mojallali, H.: An ADRC-based backstepping control design for a class of fractional-order systems. ISA Transactions 121, 140–146 (2022)

    Article  Google Scholar 

  10. Kanellakopoulos, I., Kokotovic, P.V., Morse, A.S.: “Systematic design of adaptive controllers for feedback linearizable systems.” In: 1991 American control conference, pp. 649–654, IEEE (1991)

  11. Lv, M., De Schutter, B., Cao, J., Baldi, S.: Adaptive prescribed performance asymptotic tracking for high-order odd-rational-power nonlinear systems. IEEE Transactions on Automatic Control, 1–1 (2022). https://doi.org/10.1109/TAC.2022.3147271

  12. Wang, P., Yu, W., Wen, G., Yu, X., Huang, T.: A chattering free consensus controller for multiple Lur’e systems with a non-autonomous leader and directed switching topology. Science China Technological Sciences (2021). https://doi.org/10.1007/s11431-022-2175-5

    Article  Google Scholar 

  13. Soleymanpour, S., Navabi, M.: “Integrated adaptive backstepping attitude control of spacecraft.” In: 2017 IEEE 4th International Conference on Knowledge-Based Engineering and Innovation (KBEI), pp. 0949–0954, IEEE (2017)

  14. Lv, M., Yu, W., Cao, J., Baldi, S.: A separation-based methodology to consensus tracking of switched high-order nonlinear multiagent systems. IEEE Transactions on Neural Networks and Learning Systems, 1–13 (2021). https://doi.org/10.1109/TNNLS.2021.3070824

  15. Cui, Y., Zhang, H., Wang, Y., Gao, W.: Adaptive control for a class of uncertain strict-feedback nonlinear systems based on a generalized fuzzy hyperbolic model. Fuzzy Sets and Systems 302, 52–64 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  16. Liu, H., Pan, Y., Li, S., Chen, Y.: Adaptive fuzzy backstepping control of fractional-order nonlinear systems. IEEE Transactions on Systems, Man, and Cybernetics: Systems 47(8), 2209–2217 (2017)

    Article  Google Scholar 

  17. Wang, C., Liang, M., Chai, Y.: Adaptive control of a class of incommensurate fractional order nonlinear systems with input dead-zone. IEEE Access 7, 153710–153723 (2019)

    Article  Google Scholar 

  18. Liu, H., Pan, Y., Cao, J., Wang, H., Zhou, Y.: Adaptive neural network backstepping control of fractional-order nonlinear systems with actuator faults. IEEE Transactions on Neural Networks and Learning Systems 31(12), 5166–5177 (2020)

    Article  MathSciNet  Google Scholar 

  19. Ma, Z., Ma, H.: Reduced-order observer-based adaptive backstepping control for fractional-order uncertain nonlinear systems. IEEE Transactions on Fuzzy Systems 28(12), 3287–3301 (2020)

    Article  Google Scholar 

  20. Slotine, J.-J.E., Li, W.: Composite adaptive control of robot manipulators. Automatica 25(4), 509–519 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  21. Pan, Y., Yu, H.: Composite learning from adaptive dynamic surface control. IEEE Transactions on Automatic Control 61(9), 2603–2609 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Xu, B., Shi, Z., Yang, C., Sun, F.: Composite neural dynamic surface control of a class of uncertain nonlinear systems in strict-feedback form. IEEE Transactions on Cybernetics 44(12), 2626–2634 (2014)

    Article  Google Scholar 

  23. Pan, Y., Liu, Y., Yu, H.: Online data-driven composite adaptive backstepping control with exact differentiators. International Journal of Adaptive Control and Signal Processing 30(5), 779–789 (2016)

    Article  MathSciNet  Google Scholar 

  24. Liu, H., Pan, Y., Cao, J.: Composite learning adaptive dynamic surface control of fractional-order nonlinear systems. IEEE Transactions on Cybernetics 50(6), 2557–2567 (2019)

    Article  Google Scholar 

  25. Wang, X., Xu, B., Shi, P., Li, S.: Efficient learning control of uncertain fractional-order chaotic systems with disturbance. IEEE Transactions on Neural Networks and Learning Systems, 1–6 (2020)

  26. Xue, G., Lin, F., Li, S., Liu, H.: Composite learning control of uncertain fractional-order nonlinear systems with actuator faults based on command filtering and fuzzy approximation. International Journal of Fuzzy Systems, 1–20 (2022)

  27. Podlubny, I.: Fractional differential equations: an introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. Elsevier, Amsterdam (1998)

    MATH  Google Scholar 

  28. Dai, H., Chen, W.: New power law inequalities for fractional derivative and stability analysis of fractional order systems. Nonlinear Dynamics 87(3), 1531–1542 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  29. Wang, L.-X.: Adaptive fuzzy systems and control: design and stability analysis. Prentice-Hall, Inc., Upper Saddle River, NJ (1994)

    Google Scholar 

  30. Farrell, J.A., Polycarpou, M.M.: Adaptive approximation based control: unifying neural, fuzzy and traditional adaptive approximation approaches. John Wiley & Sons (2006)

    Book  Google Scholar 

  31. Keighobadi, J., Pahnehkolaei, S.M.A., Alfi, A., Machado, J.: Command-filtered compound FAT learning control of fractional-order nonlinear systems with input delay and external disturbances. Nonlinear Dynamics 108(1), 293–313 (2022)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China (12261009, 61967001), in part by the Innovation Project of Guangxi Graduate Education (YCSW2022251), and in part by the Xiangsihu Young Scholars Innovative Research Team of Guangxi Minzu University (2019RSCXSHQN02).

Author information

Authors and Affiliations

  1. College of Mathematics and Physics, Center for Applied Mathematics of Guangx, Guangxi Key Laboratory of Hybrid Computation and IC Design Analysis, Guangxi Minzu University, Nanning, 530006, China

    Hongling Qiu, Heng Liu & Xiulan Zhang

  2. School of Computer Science and Engineering, Sun Yat-sen University, Guangzhou, 510006, China

    Hongling Qiu & Heng Liu

Authors
  1. Hongling Qiu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Heng Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xiulan Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Heng Liu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qiu, H., Liu, H. & Zhang, X. Historical Data-Driven Composite Learning Adaptive Fuzzy Control of Fractional-Order Nonlinear Systems. Int. J. Fuzzy Syst. 25, 1156–1170 (2023). https://doi.org/10.1007/s40815-022-01430-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-022-01430-9

Keywords