Skip to main content

Advertisement

Springer Nature Link
Log in

Fuzzy Tracking Control for Discrete-Time Nonlinear Network Systems with Privacy Protection and Dynamic Quantization

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

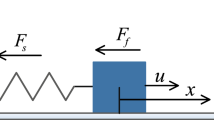
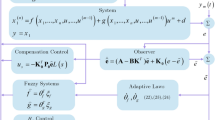
This paper investigates the problem of \({\mathcal {H}}_{\infty }\) performance output feedback tracking control of a nonlinear network control system with quantization effects in a privacy protection state. The nonlinear network system under study are represented by a Takagi–Sugeno fuzzy model. Dynamic quantization of the reference model and controlled object output signals are performed to reduce the load on the communication network. A function that converges gradually to the true value over time is used to protect the privacy of the reference model from eavesdroppers, and a tracking controller is designed to ensure that the system is asymptotically stable and has a given \({\mathcal {H}}_{\infty }\) performance. The sufficient conditions for the tracking controller are given in the form of linear matrix inequalities. Finally, the validity of the proposed method is verified using a nonlinear mass-spring-damped system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Wang, W., Postoyan, R., Nesic, D., Heemels, W.P.M.H.: Periodic event-triggered control for nonlinear networked control systems. IEEE Trans. Autom. Control. 65(2), 620–635 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  2. Gatsis, K., Pappas, G.J.: Statistical learning for analysis of networked control systems over unknown channels. Automatica. 125, 109386 (2021).

    Article  MATH  Google Scholar 

  3. Li, Z.M., Xiong, J.: Event-triggered fuzzy filtering for nonlinear networked systems with dynamic quantization and stochastic cyber attacks. ISA Trans. 121(2), 53–62 (2021)

    MathSciNet  Google Scholar 

  4. Li, Z.M., Chang, X.H.: Robust \({\cal{H} }_{\infty }\) control for networked control systems with randomly occurring uncertainties: Observer-based case. ISA Trans. 83, 13–24 (2018)

    Article  Google Scholar 

  5. Hu, S., Yue, D., Cheng, Z., Tian, E., Xie, X., Chen, X.: Co-design of dynamic event-triggered communication scheme and resilient observer-based control under aperiodic dos attacks. IEEE Trans. Cybern. 51(9), 4591–4601 (2021)

    Article  Google Scholar 

  6. Kalman, R.E.: Nonlinear aspects of sampled-data control systems. In: Proc. Symp. Nonlinear Circuit Analysis VI, pp. 273–313 (1956)

  7. Li, Z., Pan, Y., Ma, J.: Disturbance observer-based fuzzy adaptive containment control of nonlinear multi-agent systems with input quantization. Int. J. Fuzzy Syst. 24(1), 574–586 (2022)

    Article  Google Scholar 

  8. Cheng, J., Park, J.H., Wu, Z.G., Yan, H.C.: Ultimate boundedness control for networked singularly perturbed systems with deception attacks: a Markovian communication protocol approach. IEEE Trans. Netw. Sci. Eng. 9(2), 445–456 (2022)

    Article  MathSciNet  Google Scholar 

  9. Okajima, H., Sawada, K., Matsunaga, N.: Dynamic quantizer design under communication rate constraints. IEEE Trans. Autom. Control. 61(10), 3190–3196 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chang, X.H., Xue, J.: Observer-based fuzzy feedback control for nonlinear systems subject to transmission signal quantization. Appl. Math. Comput. 414, 126657 (2022). 

    Article  MathSciNet  MATH  Google Scholar 

  11. Chang, X.H., Liu, Y.: Robust \({\cal{H} }_{\infty }\) filtering for vehicle sideslip angle with quantization and data dropouts. IEEE Trans. Veh. Technol. 69(10), 10435–10445 (2020)

    Article  Google Scholar 

  12. Xiong, J., Chang, X.H., Park, J.H.: Nonfragile fault-tolerant control of suspension systems subject to input quantization and actuator fault. Int. J. Robust Nonlinear Control. 30(16), 6720-6743 (2020) 

    Article  MathSciNet  Google Scholar 

  13. Zheng, Q., Xu, S.Y., Du, B.Z.: Quantized guaranteed cost output feedback control for nonlinear networked control systems and its applications. IEEE Trans. Fuzzy Syst. 30(7), 2402–2411 (2022)

    Article  Google Scholar 

  14. Ding, S.H., Zhang, B.B., Mei, K.Q., Park, J.H.: Adaptive fuzzy SOSM controller design with output constraints. IEEE Trans. Fuzzy Syst. 30(7), 2300–2311 (2022)

    Article  Google Scholar 

  15. Chang, X.H., Qiao, M.Y., Zhao, X.D.: Fuzzy energy-to-peak filtering for continuous-time nonlinear singular system. IEEE Trans. Fuzzy Syst. 30(7), 2325-2336. (2021)

    Article  Google Scholar 

  16. Wang, J., Yang, C.Y., Xia, J.W., Wu, Z.G., Shen, H.: Observer-based sliding mode control for networked fuzzy singularly perturbed systems under weighted try-once-discard protocol. IEEE Trans. Fuzzy Syst. 30(6), 1889–1899 (2022)

    Article  Google Scholar 

  17. Farbood, M., Shasadeghi, M., Niknam, T., Safarinejadian, B.: Fuzzy lyapunov-based model predictive sliding mode control of nonlinear systems: an ellipsoid recursive feasibility approach. IEEE Trans. Fuzzy Syst. 30(16), 1929-1938 (2021)

    Article  Google Scholar 

  18. Chang, X.H., Yang, G.H.: Nonfragile \({\cal{H} }_{\infty }\) filter design for T-S fuzzy systems in standard form. IEEE Trans. Ind. Electron. 61(7), 3448–3458 (2014)

    Article  Google Scholar 

  19. Zheng, Q.X., Xu, S.Y., Zhang, Z.Q.: Nonfragile quantized \({\cal{H} }_\infty\) filtering for discrete-time switched T-S fuzzy systems with local nonlinear models. IEEE Trans. Fuzzy Syst. 29(6), 1507–1517 (2020)

    Article  Google Scholar 

  20. Feng, Z.G., Zhang, H.Y., Lam, H.K.: New results on dissipative control for a class of singular Takagi-Sugeno fuzzy systems with time delay. IIEEE Trans. Fuzzy Syst. 30(7), 2466–2475 (2021)

    Article  Google Scholar 

  21. Markus, L.: Asymptotically autonomous differential systems. Ann. Math. Stud. 36(6), 542 (1956)

    MathSciNet  MATH  Google Scholar 

  22. Artstein, Z.: Appendix a: limiting equations and stability of nonautonomous ordinary differential equations. In: The Stability of Dynamical Systems, pp. 57–76. Elsevier (1976)

  23. Dwork, C.: Differential privacy. In: Proceedings of the 33rd International Conference on Automata, Languages and Programming-Volume Part II, pp. 1–12. Springer (2006)

  24. Ambrosin, M., Braca, P., Conti, M., Lazzeretti, R.: Odin: O bfuscation-based privacy-preserving consensus algorithm for decentralized information fusion in smart device networks. ACM Trans. Int. Technol. 18(1), 1–22 (2017)

    Article  Google Scholar 

  25. Lazzeretti, R., Horn, S., Braca, P., Willett, P.: Secure multi-party consensus gossip algorithms. In: IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 7406–7410 (2014)

  26. Ruan, M., Gao, H., Wang, Y.: Secure and privacy-preserving consensus. IEEE Trans. Autom. Control. 64(10), 4035–4049 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  27. Ren, W., Xiong, J.: Tracking control of nonlinear networked and quantized control systems with communication delays. IEEE Trans. Autom. Control. 65(8), 3685–3692 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  28. Zou, A.M., Kumar, K.D., Ruiter, A.: Fixed-time attitude tracking control for rigid spacecraft. Automatica. 113, 108792 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  29. Li, Y., Shao, X., Tong, S.: Adaptive fuzzy prescribed performance control of nontriangular structure nonlinear systems. IEEE Trans. Fuzzy Syst. 28(10), 2416–2426 (2020)

    Article  Google Scholar 

  30. Feng, S.S., Sun, Z.Y., Zhou, C.Q., Chen, C.C., Meng, Q.: Output tracking control via neural networks for high-order stochastic nonlinear systems with dynamic uncertainties. Int. J. Fuzzy Syst. 23(3), 716–726 (2021)

    Article  Google Scholar 

  31. Postoyan, R., Wouw, V.D.N., Nesic, D., Heemels, W.P.M.H.: Tracking control for nonlinear networked control systems. IEEE Trans. Autom. Control. 59(6), 1539–1554 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  32. Wouw, V.D.N., Naghshtabrizi, P., Cloosterman, M., Hespanha, J.: Tracking control for sampled-data systems with uncertain time-varying sampling intervals and delays. Int. J. Robust Nonlinear Control. 20(4), 387–411 (2010)

    MathSciNet  MATH  Google Scholar 

  33. Meng, J.E., Deng, C., Su, S.F., Wang, N.: Fuzzy synchronization control of complex dynamical networks under network attacks and actuator faults. Int. J. Fuzzy Syst. 21(7), 2043–2053 (2019)

    Article  MathSciNet  Google Scholar 

  34. Chen, Q.X., Chang, X.H.: Resilient filter of nonlinear network systems with dynamic event-triggered mechanism and hybrid cyber attack. Appl. Math. Comput. 434, 127419 (2022). 

    Article  MathSciNet  MATH  Google Scholar 

  35. Wang, F., Chen, B., Lin, C., Zhang, J., Meng, X.: Adaptive neural network finite-time output feedback control of quantized nonlinear systems. IEEE Trans. Cybern. 48(6), 1839–1848 (2018)

    Article  Google Scholar 

  36. Li, Y., Min, X., Tong, S.: Observer-based fuzzy adaptive inverse optimal output feedback control for uncertain nonlinear systems. IEEE Trans. Fuzzy Syst. 29(6), 1484–1495 (2021)

    Article  Google Scholar 

  37. Altafini, C.: A system-theoretic framework for privacy preservation in continuous-time multiagent dynamics. Automatica. 122, 109253 (2020) 

    Article  MathSciNet  MATH  Google Scholar 

  38. Liu, J., Wei, L., Xie, X., Tian, E., Fei, S.: Quantized stabilization for T-S fuzzy systems with hybrid-triggered mechanism and stochastic cyber-attacks. IEEE Trans. Fuzzy Syst. 26(6), 3820–3834 (2018)

    Article  Google Scholar 

  39. Chang, X.H., Liu, Y.: Quantized output feedback control of AFS for electric vehicles with transmission delay and data dropouts. IEEE Trans. Intell Transp. Syst. 23(9), 16026–16037 (2022)

    Article  Google Scholar 

  40. Chang, X.H., Yang, C., Xiong, J.: Quantized fuzzy output feedback \({\cal{H} }_{\infty }\) control for nonlinear systems with adjustment of dynamic parameters. IEEE Trans. Syst. Man Cybern. Syst. 49(10), 2005–2015 (2019)

    Article  Google Scholar 

  41. Tanaka, K., Ikeda, T., Wang, H.: Robust stabilization of a class of uncertain nonlinear systems via fuzzy control: quadratic stabilizability, \({\cal{H} }_{\infty }\) control theory, and linear matrix inequalities. IEEE Trans. Fuzzy Syst. 4(1), 1–13 (1996)

    Article  Google Scholar 

Download references

Funding

The work was supported in part by the Liaoning BaiQianWan Talents Program of China under Grant 2018049, the Joint Project of Key Laboratory of Liaoning Province of China under Grant 2019-KF-03-12 and the Science and Technology Research Project of Liaoning Provincial Education Department of China under Grant LJKZ1032.

Author information

Authors and Affiliations

  1. College of Control Science and Engineering, Bohai University, Jinzhou, 121013, Liaoning, China

    Mingquan Li & Xiaoheng Chang

Authors
  1. Mingquan Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Xiaoheng Chang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Xiaoheng Chang.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, M., Chang, X. Fuzzy Tracking Control for Discrete-Time Nonlinear Network Systems with Privacy Protection and Dynamic Quantization. Int. J. Fuzzy Syst. 25, 1227–1238 (2023). https://doi.org/10.1007/s40815-022-01436-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-022-01436-3

Keywords