Observer-Based Robust Adaptive TS Fuzzy Control of Uncertain Systems with High-Order Input Derivatives and Nonlinear Input–Output Relationships

Abstract

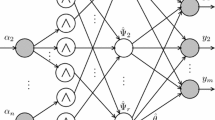
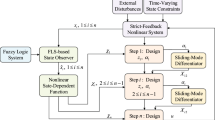
The conventional state-space form often leads to control design strategies and stability analysis techniques generally applicable to dynamical processes. Nevertheless, it may also lead to higher model complexity and loss of interpretability. Here, we skip this representation for nonlinear dynamical systems with high-order input derivatives and nonlinear input–output relationships. Specifically, we incorporate the principle of ${H}_{\infty }$ design within an observer-based adaptive fuzzy controller to guarantee robust stabilization and trajectory tracking for such nonlinear systems. The proposed approach has four integral components. Firstly, zero-order Takagi–Sugeno fuzzy systems approximate nonlinear and uncertain functions by the estimated states of the observer. Secondly, the ${H}_{\infty }$ control attenuates fuzzy approximation errors, observer errors, and environmental effects to a prescribed attenuation level. Thirdly, the adaptive laws and the ${H}_{\infty }$ term are met with simple equations, avoiding the positive definite matrices in Lyapunov equations. Fourthly, a compensation term is added to ensure the stability of the closed-loop system. Fifthly, the Lyapunov theory guarantees the asymptotic stability of the overall system and the ${H}_{\infty }$ tracking performance of the output. Finally, the proposed method is applied to two unknown nonlinear systems under disturbances, noises, packet loss, and asymmetric dead-zone. The first is a second-order spring-mass-damper trolley system, and the second is a third-order nonlinear system. Comparing the results with a recent competing controller reveals that the proposed approach improves transparency and lowers tunable parameters, fuzzy basis functions dimension, the observation and tracking errors, the consumed energies, and the settling times.