Skip to main content

Advertisement

Springer Nature Link
Log in

Belief Structure-Based Pythagorean Fuzzy LINMAP for Multi-Attribute Group Decision-Making with Spatial Information

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

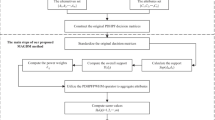
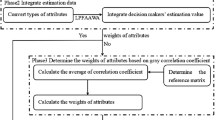
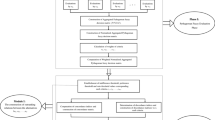
Pythagorean fuzzy sets have higher performance in expressing uncertainty information in multi-attribute group decision-making (MAGDM). The linear programming technique for multidimensional analysis of preference (LINMAP) is a prototypical compromising model that adjusts the deviation between objective assessments and subjective preferences on decision alternatives. However, the disadvantages of Pythagorean fuzzy sets in conflict measure and LINMAP model in inconsistent decision information structure have not been solved yet. To solve the problems that incomplete decision information in Pythagorean fuzzy set and inconsistent evaluation structure in LINMAP, the spatial measures and Dempster-Shafer evidence theory are introduced. A new spatial structure conflict measure is thus presented, and the belief structure of Dempster-Shafer evidence theory is used to provide a unified decision-making framework for LINMAP inconsistent evaluation structure. Firstly, a novel spatial distance measurement method is developed. Secondly, comprehensive closeness is introduced to measure individual order consistency and inconsistency between subjective preference and objective evaluation. Thirdly, we define the objective basic probability assignment and subjective basic probability assignment based on Dempster-Shafer belief structure to develop the bi-objective LINMAP of Pythagorean fuzzy sets and add the deviance between individual goodness of fit and poorness of fit is introduced as constraints to obtain the optimal attribution weights. Then, the final order of decision alternatives can be obtained by the fusion rules of Dempster-Shafer. Finally, we verify that the proposed method can improve the alternative discrimination in the case of unstable order, and the result of alternative order total biased of the proposed method is reduced by at least 80% compared with the comparative method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

Data openly available in a public repository.

References

  1. Zahid, K., Akram, M., Kahraman, C.: A new ELECTRE-based method for group decision-making with complex spherical fuzzy information. Knowl Based Syst. 243, 108525 (2022)

    Google Scholar 

  2. Ming, T., Liao, H.C.: From conventional group decision making to large-scale group decision making: what are the challenges and how to meet them in big data era? A state-of-the-art survey. Omega 100, 102141 (2021)

    Google Scholar 

  3. Yager, R.R., Abbasov, A.M.: Pythagorean membership grades, complex numbers, and decision making. Int. J. Intell. Syst. 28(5), 436–452 (2013)

    Google Scholar 

  4. Hendiani, S., Lev, B., Gharehbaghi, A.: Diagnosing social failures in sustainable supply chains using a modified pythagorean fuzzy distance to ideal solution. Comput. Ind. Eng. 154, 107156 (2021)

    Google Scholar 

  5. Dempster, A.P.: Upper and lower probabilities induced by a multivalued mapping. Ann. Math. Stat. 38, 325–339 (1967)

    MathSciNet  MATH  Google Scholar 

  6. Dymova, L., Krzysztof, K., Pavel, S.: An extension of rule base evidential reasoning in the interval-valued intuitionistic fuzzy setting applied to the type 2 diabetes diagnostic. Expert Syst. Appl. 201, 117100 (2022)

    Google Scholar 

  7. Yang, L.H., Liu, J., Ye, F.F., Wang, Y.M., Nugent, C., Wang, H., Martínez, L.: Highly explainable cumulative belief rule-based system with effective rule-base modeling and inference scheme. Knowl Based Syst. 240, 107805 (2022)

    Google Scholar 

  8. Dag, A.Z., Akcam, Z., Kibis, E., Simsek, S., Delen, D.: A probabilistic data analytics methodology based on Bayesian belief network for predicting and understanding breast cancer survival. Knowl Based Syst. 242, 108407 (2022)

    Google Scholar 

  9. Krishankumaar, R., Mishra, A.R., Gou, X., Ravichandran, K.S.: New ranking model with evidence theory under probabilistic hesitant fuzzy context and unknown weights. Neural Comput. Appl. 34, 1–15 (2022)

    Google Scholar 

  10. Petturiti, D., Vantaggi, B.: Conditional decisions under objective and subjective ambiguity in Dempster-Shafer theory. Fuzzy Sets Syst. (2022). https://doi.org/10.1016/j.fss.2022.02.011

    Article  MathSciNet  MATH  Google Scholar 

  11. Zhang, Y.X., Hao, Z.N., Xu, Z.S., Zeng, X.J., Xu, X.X.: A process-oriented probabilistic linguistic decision-making model with unknown attribute weights. Knowl-Based Syst. 235, 107594 (2022)

    Google Scholar 

  12. Rong, L.L., Wang, L., Liu, P.D.: Supermarket fresh food suppliers evaluation and selection with multigranularity unbalanced hesitant fuzzy linguistic information based on prospect theory and evidential theory. Int. J. Intell. Syst. 37(3), 1931–1971 (2022)

    Google Scholar 

  13. Liu, P.D., Zhang, X.H.: A new hesitant fuzzy linguistic approach for multiple attribute decision making based on Dempster-Shafer evidence theory. Appl. Soft Comput. 86, 105897 (2020)

    Google Scholar 

  14. Li, X.H., Chen, X.H.: Belief structure-based induced aggregation operators in decision making with hesitant fuzzy information. Neural Comput Appl. 31(12), 8917–8929 (2019)

    Google Scholar 

  15. Fei, L.G., Feng, Y.Q., Wang, H.L.: Modeling heterogeneous multi-attribute emergency decision-making with dempster-shafer theory. Comput. Ind. Eng. 161, 107633 (2021)

    Google Scholar 

  16. Chen, T.Y.: Pythagorean fuzzy linear programming technique for multidimensional analysis of preference using a squared-distance-based approach for multiple criteria decision analysis. Expert Syst. Appl. 164, 113908 (2021)

    Google Scholar 

  17. Pereiraa, M.A., Camanhoc, A.S., Figueiraa, J.R., Marques, R.C.: Incorporating preference information in a range directional composite indicator: the case of Portuguese public hospitals. Eur. J. Oper. Res. 294(2), 633–650 (2021)

    MathSciNet  Google Scholar 

  18. Srinivasan, V., Shocker, A.D.: Linear programming techniques for multi-dimensional analysis of preferences. Psychometrika 38(3), 337–369 (1973)

    MathSciNet  MATH  Google Scholar 

  19. Haghighi, M.H., Mousavi, S.M., Mohagheghi, V.: A new soft computing model based on linear assignment and linear programming technique for multidimensional analysis of preference with interval type-2 fuzzy sets. Appl. Soft Comput. 77, 780–796 (2019)

    Google Scholar 

  20. Wu, Z., Xu, J.: Managing consistency and consensus in group decision making with hesitant fuzzy linguistic preference relations. Omega 65, 28–40 (2016)

    Google Scholar 

  21. Ju, D.: Hesitant fuzzy 2-dimension linguistic programming technique for multidimensional analysis of preference for multicriteria group decision making. Mathematics. 9(24), 3196 (2021)

    Google Scholar 

  22. Liu, A.H., Wan, S.P., Dong, J.Y.: An axiomatic design-based mathematical programming method for heterogeneous multi-criteria group decision making with linguistic fuzzy truth degrees. Inform. Sci. 571, 649–675 (2021)

    MathSciNet  Google Scholar 

  23. Dong, J.Y., Wan, S.P., Chen, S.M.: Fuzzy best-worst method based on triangular fuzzy numbers for multi-criteria decision-making. Inform. Sci. 547, 1080–1104 (2021)

    MathSciNet  MATH  Google Scholar 

  24. Yang, Y.J., Francisco, C.: Consistency of 2D and 3D distances of intuitionistic fuzzy sets. Expert Syst. Appl. 39(10), 8665–8670 (2012)

    Google Scholar 

  25. Wan, S.P., Jin, Z., Dong, J.Y.: Pythagorean fuzzy mathematical programming method for multi-attribute group decision making with Pythagorean fuzzy truth degrees. Knowl. Inf. Syst. 55(2), 437–466 (2018)

    Google Scholar 

  26. Li, D., Zeng, W.: Distance measure of pythagorean fuzzy sets. Int. J. Intell. Syst. 33(2), 348–361 (2018)

    MathSciNet  Google Scholar 

  27. Sadabadi, S.A., Hadi-Vencheh, A., Jamshidi, A., Jalali, M.: A linear programming technique to solve fuzzy multiple criteria decision making problems with an application. RAIRO-Oper. Res. 55(1), 83–97 (2021)

    MathSciNet  MATH  Google Scholar 

  28. Wang, J.C., Chen, T.Y.: A novel pythagorean fuzzy LINMAP-based compromising approach for multiple criteria group decision-making with preference over alternatives. Int. J. Comput. Int. Sys. 13(1), 444–463 (2020)

    Google Scholar 

  29. Akram, M., Luqman, A., Alcantud, J.C.R.: An integrated ELECTRE-I approach for risk evaluation with hesitant Pythagorean fuzzy information [J]. Expert Syst. Appl. 200, 116945 (2022)

    Google Scholar 

  30. Talukdar, P., Dutta, P.: Distance measures for cubic Pythagorean fuzzy sets and its applications to multicriteria decision making[J]. Granular Comput. 6(2), 267–284 (2021)

    Google Scholar 

  31. Xue, W., Xu, Z., Zhang, X., et al.: Pythagorean fuzzy LINMAP method based on the entropy theory for railway project investment decision making [J]. Int. J. Intell. Syst. 33(1), 93–125 (2018)

    Google Scholar 

  32. Khan, M.J., Ali, M.I., Kumam, P.: Improved generalized dissimilarity measure based VIKOR method for Pythagorean fuzzy sets[J]. Int. J. Intell. Syst. 37(3), 1807–1845 (2022)

    Google Scholar 

  33. Zeng, W., Li, D., Yin, Q.: Distance and similarity measures of Pythagorean fuzzy sets and their applications to multiple criteria group decision making. Int. J. Intell. Syst. 33(11), 2236–2254 (2018)

    Google Scholar 

  34. Zhou, F., Chen, T.Y.: Multiple criteria group decision analysis using a Pythagorean fuzzy programming model for multidimensional analysis of preference based on novel distance measures [J]. Comput. Ind. Eng. 148, 106670 (2020)

    Google Scholar 

  35. Zhou, F., Chen, T.Y.: An integrated multicriteria group decision-making approach for green supplier selection under Pythagorean fuzzy scenarios [J]. Ieee Access. 8, 165216–165231 (2020)

    Google Scholar 

  36. Chen, T.Y.: Multiple criteria group decision making using a parametric linear programming technique for multidimensional analysis of preference under uncertainty of Pythagorean fuzziness [J]. IEEE Access. 7, 174108–174128 (2019)

    Google Scholar 

  37. Wang, Z., Ran, Y., Chen, T.Y., Yu, H., Zhang, G.: Failure mode and effects analysis using extended matter-element model and AHP. Comput. Ind. Eng. 140, 1–8 (2020)

    Google Scholar 

  38. Sarkar, B., Biswas, A.: A unified method for Pythagorean fuzzy multicriteria group decision-making using entropy measure, linear programming and extended technique for ordering preference by similarity to ideal solution. Soft. Comput. 24(7), 5333–5344 (2019)

    MATH  Google Scholar 

  39. Liao, N., Wei, G., Chen, X.: TODIM method based on cumulative prospect theory for multiple attributes group decision making under probabilistic hesitant fuzzy setting. Int. J. Fuzzy Syst. 24, 322–339 (2022). https://doi.org/10.1007/s40815-021-01138-2

    Article  Google Scholar 

  40. Zhang, X.L., Xu, Z.S.: Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. Int. J. Intell. Syst. 29(12), 1061–1078 (2014)

    MathSciNet  Google Scholar 

  41. Kahneman, D., Tversky, A.: Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291 (1979)

    MathSciNet  MATH  Google Scholar 

  42. Farhadinia, B.: Similarity-based multi-criteria decision making technique of pythagorean fuzzy sets. Artif. Intell. Rev. 2021, 1–46 (2021)

    MathSciNet  Google Scholar 

  43. Xu, Z.S.: An overview of methods for determining OWA weights. Int. J. Intell. Syst. 20(8), 843–865 (2005)

    MATH  Google Scholar 

  44. Wang, Y., Chen, F., Zhuang, G., Yang, G.: Dynamic event-based mixed H∞ and dissipative asynchronous control for Markov jump singularly perturbed systems. Appl. Math. Comput. 386, 125443 (2020)

    MathSciNet  MATH  Google Scholar 

  45. Wang, Y., Chen, F., Zhuang, G.: Dynamic event-based reliable dissipative asynchronous control for stochastic Markov jump systems with general conditional probabilities. Nonlinear Dynam. 101, 465–485 (2020)

    Google Scholar 

  46. Mehdi, D., Marzieh, A., Elnaz, E., Alessio, I.: A probabilistic hesitant fuzzy Choquet integral-based TODIM method for multi-attribute group decision-making. Expert Syst. Appl. 191, 116266 (2022)

    Google Scholar 

  47. Wang, Y.Q., Chen, F., Zhuang, G.M., Song, G.F.: Event-based asynchronous and resilient filtering for Markov jump singularly perturbed systems against deception attacks. ISA T. 112, 56–73 (2021)

    Google Scholar 

Download references

Funding

This paper is supported by the National Natural Science Foundation of China (No. 71971117, No. 71671001) and the Ministry of education of Humanities and Social Science project of China (No. 17YJA630035).

Author information

Authors and Affiliations

  1. School of Economics and Management, Nanjing University of Science and Technology, Nanjing, 210094, People’s Republic of China

    Jiali Wang, Wenqi Jiang, Xiwen Tao & Shanshan Yang

  2. School of Economics and Management, Anhui Polytechnic University, Wuhu, 241000, People’s Republic of China

    Bengang Gong

Authors
  1. Jiali Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Wenqi Jiang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Xiwen Tao
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Bengang Gong
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Shanshan Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

JW contributed to writing—original draft, validation, software, formal analysis writing—review & editing, and visualization. WJ contributed to conceptualization, methodology, supervision, writing—review & editing, and funding acquisition. XT contributed to writing—review & editing. BG contributed to writing—review & editing and funding acquisition.

Corresponding author

Correspondence to Wenqi Jiang.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, J., Jiang, W., Tao, X. et al. Belief Structure-Based Pythagorean Fuzzy LINMAP for Multi-Attribute Group Decision-Making with Spatial Information. Int. J. Fuzzy Syst. 25, 1444–1464 (2023). https://doi.org/10.1007/s40815-022-01445-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-022-01445-2

Keywords