Skip to main content
Springer Nature Link
Log in

Interval Valued Intuitionistic Fuzzy Diagonal Optimal Algorithm to Solve Transportation Problems

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

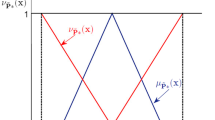
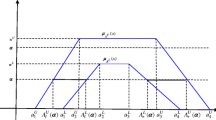
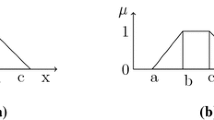Abstract

Civilization is established as a result of transportation activities all over the world. Transportation plays a major role for the economic growth of the country. An optimizer seeks to minimize the transportation cost in order to maximize the profit when dealing with transportation issues. However, the transportation costs may differ due to a variety of unforeseeable factors. To handle with the uncertainty and hesitation factors that arise in real-world transportation problems, the cost parameters of the transportation problem are modelled here as interval valued intuitionistic fuzzy numbers. To solve the transportation problem, a new subtraction operation is developed, and the diagonal optimal method is applied for interval valued triangular and trapezoidal intuitionistic fuzzy numbers. In addition, a new ordering for interval valued trapezoidal intuitionistic fuzzy numbers based on the Yager’s formula which is in the existing ordering of interval valued triangular intuitionistic fuzzy numbers is proposed. However, numerical examples demonstrate the feasibility of the proposed approach, and the obtained results are compared to existing ones.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

References

  1. Hitchcock, F.L.: The distribution of a product from several sources to numerous localities. J. Math. Phys. 20(1–4), 224–230 (1941)

    Article  MathSciNet  MATH  Google Scholar 

  2. Dantzig, G.B., Thapa, M.N.: Linear Programming 1: Introduction. Springer Science and Business Media, Berlin (1941)

    MATH  Google Scholar 

  3. Charnes, A., Cooper, W.W.: The stepping stone method of explaining linear programming calculations in transportation problems. Manag. Sci. 1(1), 49–69 (1954)

    Article  MathSciNet  MATH  Google Scholar 

  4. Zadeh, L.A.: Fuzzy sets. Inf. Control. 8(3), 338–353 (1965)

    MATH  Google Scholar 

  5. Atanassov, K.: Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20(1), 87–96 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  6. Atanassov, K., Gargov, G.: Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 31(3), 343–349 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  7. Pandian, P., Natarajan, G.: A new algorithm for finding a fuzzy optimal solution for fuzzy transportation problems. Appl. Math. Sci. 4(2), 79–90 (2010)

    MATH  Google Scholar 

  8. Kaur, A., Kumar, A.: A new approach for solving fuzzy transportation problems using generalized trapezoidal fuzzy numbers. Appl. Soft Comput. 12(3), 1201–1213 (2012)

    Article  Google Scholar 

  9. Kumar, P.S.: PSK method for solving type-1 and type-3 fuzzy transportation problems. Int. J. Fuzzy Syst. Appl. 5(4), 121–146 (2016)

    Google Scholar 

  10. Kaur, A., Kumar, A.: A new method for solving fuzzy transportation problems using ranking function. Appl. Math. Model. 35(12), 5652–5661 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  11. Biswas, A., Roy, S.K., Mondal, S.P.: Evolutionary algorithm based approach for solving transportation problems in normal and pandemic scenario. Appl. Soft Comput. 129, 109576 (2022)

    Article  Google Scholar 

  12. Angelov, P.P.: Optimization in an intuitionistic fuzzy environment. Fuzzy Sets Syst. 86(3), 299–306 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  13. Malik, M., Gupta, S. K., Ahmad, I.: A new approach to solve fully intuitionistic fuzzy linear programming problem with unrestricted decision variables. J. Intell. Fuzzy Syst. 41(6), 6053–6066 (2021)

  14. Kumar, P.S.: Intuitionistic fuzzy zero point method for solving type-2 intuitionistic fuzzy transportation problem. Int. J. Oper. Res. 37(3), 418–451 (2020)

    Article  MathSciNet  Google Scholar 

  15. Mahajan, S., Gupta, S.K.: On fully intuitionistic fuzzy multiobjective transportation problems using different membership functions. Ann. Oper. Res. 296(1), 211–241 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  16. Mahmoodirad, A., Allahviranloo, T., Niroomand, S.: A new effective solution method for fully intuitionistic fuzzy transportation problem. Soft Comput. 23(12), 4521–4530 (2019)

    Article  MATH  Google Scholar 

  17. Ebrahimnejad, A., Verdegay, J.L.: A new approach for solving fully intuitionistic fuzzy transportation problems. Fuzzy Optim. Decis. Mak. 17(4), 447–474 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  18. Kumar, P.S., Hussain, R.J.: A systematic approach for solving mixed intuitionistic fuzzy transportation problems. Int. J. Pure Appl. Math. 92(2), 181–190 (2014)

    Article  MATH  Google Scholar 

  19. Xu, Z., Zhao, N.: Information fusion for intuitionistic fuzzy decision making: an overview. Inf. Fusion 28, 10–23 (2016)

    Article  Google Scholar 

  20. Lin, L., Yuan, X.H., Xia, Z.Q.: Multicriteria fuzzy decision-making methods based on intuitionistic fuzzy sets. J. Comput. Syst. Sci. 73(1), 84–88 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  21. Bharati, S.K., Singh, S.R.: Transportation problem under interval-valued intuitionistic fuzzy environment. Int. J. Fuzzy Syst. 20(5), 1511–1522 (2018)

    Article  Google Scholar 

  22. Bharati, S.K., Singh, S.R.: A new interval-valued intuitionistic fuzzy numbers: ranking methodology and application. New Math. Nat. Comput. 14(03), 363–381 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  23. Dhanasekar, S., Rani, J.J., Annamalai, M.: Transportation Problem for Interval-Valued Trapezoidal Intuitionistic Fuzzy Numbers. Int. J. Fuzzy Log. Intell. Syst. 22(2), 155–168 (2022)

    Article  Google Scholar 

  24. Mitchell, H.B.: Ranking-intuitionistic fuzzy numbers. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 12(03), 377–386 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  25. Bharati, S.K.: Ranking method of intuitionistic fuzzy numbers. Glob. J. Pure Appl. Math. 13(9), 4595–4608 (2017)

    MathSciNet  Google Scholar 

  26. Nayagam, V.L.G., Sivaraman, G.: Ranking of interval-valued intuitionistic fuzzy sets. Appl. Soft Comput. 11(4), 3368–3372 (2011)

    Article  Google Scholar 

  27. Ze-Shui, X.: Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis. 2, 0–19 (2007)

    Google Scholar 

  28. Bharati, S.K.: Transportation problem with interval-valued intuitionistic fuzzy sets: impact of a new ranking. Prog. Artif. Intell. 10(2), 129–145 (2021)

    Article  MathSciNet  Google Scholar 

  29. Wang, X.: Fuzzy optimal assignment problem. Fuzzy Math 3, 101–108 (1987)

    MathSciNet  MATH  Google Scholar 

  30. Lin, C.J., Wen, U.P.: A labeling algorithm for the fuzzy assignment problem. Fuzzy Sets Syst. 142(3), 373–391 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  31. Khalid, M., Sultana, M., Zaidi, F.: A new diagonal optimal approach for assignment problem. Appl. Math. Sci. 8(160), 7979–7986 (2014)

    Google Scholar 

  32. Dhanasekar, S., Manivannan, A., Parthiban, V., Gururaj, A.D.M.: A Fuzzy VAM-diagonal optimal algorithm to solve fuzzy assignment problem. Int. J. Mech. Eng. Technol. 10(2), 1282–1287 (2019)

    Google Scholar 

  33. Purushothkumar, M.K., Ananathanarayanan, M., Dhanasekar, S.: A diagonal optimal algorithm to solve interval integer transportation problems. Int. J. Appl. Eng. Res. 13(18), 13702–13704 (2018)

    Google Scholar 

  34. Purushothkumar, M.K., Ananathanarayanan, M., Dhanasekar, S.: Fuzzy diagonal optimal algorithm to solve fully fuzzy transportation problems. ARPN J. Eng. Appl. Sci 14(19), 3450–3454 (2019)

    Google Scholar 

  35. Yager, R.R.: A procedure for ordering fuzzy subsets of the unit interval. Inf. Sci. 24(2), 143–161 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  36. Atanassov, K.T.: New operations defined over the intuitionistic fuzzy sets. Fuzzy Sets Syst. 61(2), 137–142 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  37. Dong, J.Y., Wan, S.P.: Interval-valued trapezoidal intuitionistic fuzzy generalized aggregation operators and application to multi-attribute group decision making. Sci. Iran. 22(6), 2702–2715 (2015)

    Google Scholar 

Download references

Author information

Author notes

  1. J. Jansi Rani and A. Manivannan have contributed equally to this work.

Authors and Affiliations

  1. School of Advanced Sciences, Vellore Institute of Technology, Chennai, Chennai, Tamil Nadu, 600127, India

    J. Jansi Rani, A. Manivannan & S. Dhanasekar

Authors
  1. J. Jansi Rani
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. A. Manivannan
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. S. Dhanasekar
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to S. Dhanasekar.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jansi Rani, J., Manivannan, A. & Dhanasekar, S. Interval Valued Intuitionistic Fuzzy Diagonal Optimal Algorithm to Solve Transportation Problems. Int. J. Fuzzy Syst. 25, 1465–1479 (2023). https://doi.org/10.1007/s40815-022-01446-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-022-01446-1

Keywords