Skip to main content
SpringerLink
Log in

Optimal Output Agreement for T-S Fuzzy Multi-agent Systems: An Adaptive Distributed Approach

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

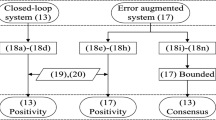
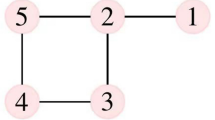
This paper studies the distributed optimal output agreement problem of T-S fuzzy multi-agent systems under a weight-balanced and quasi-strongly connected graph. Consider a given global convex objective function, the objective of this paper is to steer the outputs of T-S fuzzy multi-agent systems to the optimal solution of this global objective function by the partial information of the local objective functions. To achieve the objective, a novel T-S fuzzy adaptive distributed optimal algorithm is proposed to guarantee that outputs of all agents can follow the global optimal solution. Then, the stability of overall closed-loop system composed of T-S fuzzy multi-agent systems and T-S fuzzy adaptive distributed scheme is established. In order to achieve the output agreement and minimize the objective function simultaneously, a sufficient condition is obtained. Finally, a numerical example is employed to demonstrate the effectiveness and superiority of the theoretical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Wang, Z.J., Zhan, Z.H., Kwong, S., Jin, H., Zhang, J.: Adaptive granularity learning distributed particle swarm optimization for large-scale optimization. IEEE Trans. Cybern. 51(3), 1175–1188 (2021)

    Article  Google Scholar 

  2. Kumar, R., Sharma, V.K.: Whale optimization controller for load frequency control of a two-area multi-source deregulated power system. Int. J. Fuzzy Syst. 22, 122–137 (2020)

    Article  Google Scholar 

  3. Chen, W., Xu, W.: A hybrid multiobjective bat algorithm for fuzzy portfolio optimization with real-world constraints. Int. J. Fuzzy Syst. 21, 291–307 (2019)

    Article  MathSciNet  Google Scholar 

  4. Ram, S.S., Veeravalli, V.V., Nedić, A.: Distributed and recursive parameter estimation in parametrized linear state-space models. IEEE Trans Autom Control. 55(2), 488–492 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  5. Cortés, J., Bullo, F.: Coordination and geometric optimization via distributed dynamical systems. SIAM J. Control Optim. 44, 1543–1574 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  6. Kia, S.S., Cortés, J., Martínez, S.: Distributed convex optimization via continuous-time coordination algorithms with discrete-time communication. Automatica. 55, 254–264 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  7. Nedić, A., Ozdaglar, A.: Distributed subgradient methods for multi-agent optimization. IEEE Trans. Autom. Control. 54(1), 48–61 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Nguyen, X., Jordan, M.I., Sinopoli, B.: A kernel-based learning approach to ad hoc sensor network localization. ACM Trans. Sensor Netw. 1(1), 134–152 (2005)

    Article  Google Scholar 

  9. Lobel, I., Ozdaglar, A.: Distributed subgradient methods for convex optimization over random networks. IEEE Trans. Autom. Control. 56(6), 1291–1306 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  10. Duchi, J.C., Agarwal, A., Wainwright, M.J.: Dual averaging for distributed optimization: convergence analysis and network scaling. IEEE Trans. Autom. Control. 57(3), 52–606 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  11. Gharesifard, B., Corts, J.: Distributed continuous-time convex optimization on weight-balanced digraphs. IEEE Trans. Autom. Control. 59(3), 781–786 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  12. Lu, J., Tang, C.Y.: Zero-gradient-sum algorithms for distributed convex optimization: The continuous-time case. IEEE Trans. Autom. Control. 57(9), 2348–2354 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  13. Jin, Z.H., Sun, X.J., Qin, Z.Y., Ahn, C.K.: Fuzzy small-gain approach for the distributed optimization of T-S fuzzy cyber-physical systems. IEEE Trans. Cybern. (2022). https://doi.org/10.1109/TCYB.2022.3202576

    Article  Google Scholar 

  14. Hatanaka, T., Chopra, N., Ishizaki, T., Li, N.: Passivity-based distributed optimization with communication delays using PI consensus algorithm. IEEE Trans. Autom. Control. 63(12), 4421–4428 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  15. Wang, X.F., Teel, A.R., Liu, K.Z., Sun, X.M.: Stability analysis of distributed convex optimization under persistent attacks: a hybrid systems approach. Automatica. 111, 108607 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  16. Li, W.J., Zeng, X.L., Hong, Y.G., Ji, H.B.: Distributed consensus-based solver for semi-definite programming: an optimization viewpoint. Automatica. 131, 109737 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  17. Wang, X.L., Yang, G.H.: Piecewise attack strategy design for T-S fuzzy cyber-physical systems. IEEE Trans. Syst. Man Cybern.: Syst. (2022). https://doi.org/10.1109/TSMC.2022.3146282

    Article  Google Scholar 

  18. Jin, Z.H., Wang, Z.X., Zhang, X.F.: Cooperative control problem of Takagi-Sugeno fuzzy multiagent systems via observer based distributed adaptive sliding mode control. J. Franklin Instit. 359(8), 3405–3426 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  19. Zhang, J.X., Yang, G.H.: Fuzzy adaptive output feedback control of uncertain nonlinear systems with prescribed performance. IEEE Trans. Cybern. 48(5), 1342–1354 (2018)

    Article  Google Scholar 

  20. Li, R.C., Zhang, X.F.: Adaptive sliding mode observer design for a class of T-S fuzzy descriptor fractional order systems. IEEE Trans. Fuzzy Syst. 28(9), 1951–1959 (2020)

    Article  Google Scholar 

  21. Zhang, X.F., Zhao, Z.L.: Normalization and stabilization for rectangular singular fractional order T-S fuzzy systems. Fuzzy Sets Syst. 38, 140–153 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  22. Liang, H.J., Chen, L., Pan, Y.N., Lam, H.K.: Fuzzy-based robust precision consensus tracking for uncertain networked systems with cooperative-antagonistic interactions. IEEE Trans. Fuzzy Syst. (2022). https://doi.org/10.1109/TFUZZ.2022.3200730

    Article  Google Scholar 

  23. Zhang, R.M., Zeng, D.Q., Park, J.H., Lam, H.K., Xie, X.P.: Fuzzy sampled-data control for synchronization of T-S fuzzy reaction-diffusion neural networks with additive time-varying delays. IEEE Trans. Cybern. 51(5), 2384–2397 (2021)

    Article  Google Scholar 

  24. Teh, C.Y., Kerk, Y.W., Tay, K.M., Lim, C.P.: On modeling of data-driven monotone zero-order TSK fuzzy inference systems using a system identification framework. IEEE Trans. Fuzzy Syst. 26(6), 3860–3874 (2018)

    Google Scholar 

  25. Li, Z., Pan, Y., Ma, J.: Disturbance observer-based fuzzy adaptive containment control of nonlinear multi-agent systems with input quantization. Int. J. Fuzzy Syst. 24, 574–586 (2022)

    Article  Google Scholar 

  26. Jin, Z.H., Qin, Z.Y., Zhang, X.F., Guan, C.: A leader-following consensus problem via a distributed observer and fuzzy input-to-output small-gain theorem. IEEE Trans. Control Netw. Syst. 9(1), 62–74 (2022)

    Article  MathSciNet  Google Scholar 

  27. Zhou, Q., Li, H.Y., Wu, C.W., Wang, L.J., Ahn, C.K.: Adaptive fuzzy control of nonlinear systems with unmodeled dynamics and input saturation using small-gain approach. IEEE Trans. Syst. Man Cybern. Syst. 47(8), 1979–1989 (2017)

    Article  Google Scholar 

  28. Jin, Z.H., Wang, Z.X., Li, J.W.: Input-to-state stability of the nonlinear fuzzy systems via small-gain theorem and decentralized sliding mode control. IEEE Trans. Fuzzy Syst. (2021). https://doi.org/10.1109/TFUZZ.2021.3099036

    Article  Google Scholar 

  29. Zhang, J.X., Yang, G.H.: Fault-tolerant output-constrained control of unknown Euler-Lagrange systems with prescribed tracking accuracy. Automatica. 111, 108606 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  30. Jin, Z.H., Ahn, C.K., Li, J.W.: Momentum-based distributed continuous-time nonconvex optimization of nonlinear multi-agent systems via timescale separation. IEEE Trans. Netw. Sci. Eng. (2022). https://doi.org/10.1109/TNSE.2022.3225409

    Article  Google Scholar 

  31. Zhang, J.X., Yang, G.H.: Fault-tolerant fixed-time trajectory tracking control of autonomous surface vessels with specified accuracy. IEEE Trans. Ind. Electron. 67(6), 4889–4899 (2020)

    Article  Google Scholar 

  32. Wu, H., Li, J., Chen, J.: Distributed adaptive iterative learning consensus for uncertain topological multi-agent systems based on T-S fuzzy models. Int. J. Fuzzy Syst. 20, 2605–2619 (2018)

    Article  MathSciNet  Google Scholar 

  33. Humblet, P.A.: A distributed algorithm for minimum weight directed spanning trees. IEEE Trans. Commun. 31(6), 756–762 (2003)

    Article  Google Scholar 

  34. Chen, G., Li, Z.Y.: A fixed-time convergent algorithm for distributed convex optimization in multi-agent systems. Automatica. 95, 539–543 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  35. Yu, W.W., Liu, H.Z., Zheng, W.X., Zhu, Y.N.: Distributed discrete-time convex optimization with nonidentical local constraints over time-varying unbalanced directed graphs. Automatica. 134, 109899 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  36. Liu, L.F., Qin, Z.Y., Hong, Y.G., Jiang, Z.-P.: Distributed optimization of nonlinear multi-agent systems: a small-gain approach. IEEE Trans. Autom. Control. 67(2), 676–691 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  37. Xie, W.-B., Zheng, H., Li, M.-Y., Ahn, C.K.: Membership function-dependent local controller design for T-S fuzzy systems. IEEE Trans. Sys. Man Cybern. Syst. 52(2), 814–821 (2022)

    Article  Google Scholar 

  38. Huang, B.M., Zuo, Y., Meng, Z.Y., Ren, W.: Distributed time-varying convex optimization for a class of nonlinear multiagent systems. IEEE Trans Autom. Control. 65(2), 801–808 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  39. Liu, Y., Yang, G.H.: Distributed robust adaptive optimization for nonlinear multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 51(2), 1046–1053 (2021)

    Article  Google Scholar 

  40. Chakraborty, J., Konar, A., Chakraborty, U.K., Jain, L.C.: Distributed cooperative multi-robot path planning using differential evolution. In: 2008 IEEE congress on evolutionary computation. IEEE World Congress on Computational Intelligence. pp. 718–725 (2018)

  41. An, L.W., Yang, G.H.: Distributed optimal coordination for heterogeneous linear multi-agent systems. IEEE Trans. Autom. Control. (2021). https://doi.org/10.1109/TAC.2021.3133269

    Article  Google Scholar 

  42. Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University, Cambridge (2004)

    Book  MATH  Google Scholar 

  43. Zhao, Y., Liu, Y., Wen, G., Chen, G.: Distributed optimization for linear multiagent systems: edge- and node-based adaptive designs. IEEE Trans. Autom. Control. 62(7), 3602–3609 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  44. Jia, X.C., Zhang, D.W., Hao, X.H., Zheng, N.N.: Fuzzy \(H_\infty\) tracking control for nonlinear networked control systems in T-S fuzzy model. IEEE Trans. Syst. Man Cybern. (Cybern.) 39(4), 1073–1079 (2009)

    Article  Google Scholar 

  45. Li, S.L., Nian, X.H., Deng, Z.H.: Distributed optimization of second-order nonlinear multi-agent systems with event-triggered communication. IEEE Trans. Control Netw. Syst. (2021). https://doi.org/10.1109/TCNS.2021.3092832

    Article  Google Scholar 

  46. Liang, H.J., Du, Z.X., Huang, T.W., Pan, Y.N.: Neuroadaptive performance guaranteed control for multiagent systems with power integrators and unknown measurement sensitivity. IEEE Trans. Neural Netw. Learn. Syst. (2022). https://doi.org/10.1109/TNNLS.2022.3160532

    Article  Google Scholar 

  47. Li, Z.H., Ding, Z.T., Sun, J.Y., Li, Z.K.: Distributed adaptive convex optimization on directed graphs via continuous-time algorithms. IEEE Trans. Autom. Control. 63(5), 1434–1441 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  48. Paden, B., Sastry, S.: A calculus for computing Filippov’s differential inclusion with application to the variable structure control of robot manipulators. IEEE Trans. Circuits Syst. 34(1), 73–82 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  49. Godsil, C., Royle, G.: Algebraic Graph Theory. Springer, New York (2001)

    Book  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by National Nature Science Foundation of China under Grant U1911401. Thanks to Professor Tengfei Liu and Changyun Wen for their guidance and help

Author information

Author notes

  1. Zhenghong Jin and Yi Zhang have contributed equally to this work.

Authors and Affiliations

  1. The School of Science, Shenyang University of Technology, Shenyang, 110870, Liaoning, China

    Jiawen Li & Yi Zhang

  2. The State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang, 110819, Liaoning, China

    Zhenghong Jin

  3. The School of Electrical and Electronic Engineering, Nanyang Technological University, Singapore, 639798, Singapore

    Zhenghong Jin

Authors
  1. Jiawen Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhenghong Jin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yi Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Zhenghong Jin or Yi Zhang.

Ethics declarations

Conflict of interest

We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, J., Jin, Z. & Zhang, Y. Optimal Output Agreement for T-S Fuzzy Multi-agent Systems: An Adaptive Distributed Approach. Int. J. Fuzzy Syst. 25, 2453–2463 (2023). https://doi.org/10.1007/s40815-023-01493-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-023-01493-2

Keywords

Search

Navigation