Skip to main content

Advertisement

Springer Nature Link
Log in

Fuzzy Adaptive Super-Twisting Sliding Mode Asymptotic Tracking Control of Robotic Manipulators

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

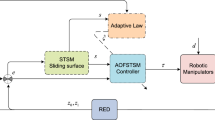
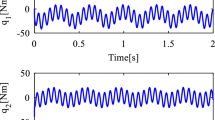
In this paper, a novel fuzzy adaptive sliding mode control method is proposed for realizing the asymptotic trajectory tracking of robotic manipulators with control backlash and uncertainties. The fuzzy logic system is introduced into the sliding mode control to estimate the system uncertainties. For compensating the unknown lumped disturbance and accelerating the convergence process, an adaptive super-twisting sliding mode controller is proposed with a novel adaptive law. The system states reach the sliding mode surface in a finite time and the control effect is continuous without over-estimation and control chattering. Depending on the Lyapunov stability theory, the tracking error converges to zero in a fast-exponential form. The effectiveness of the proposed method is fully indicated by the simulation of a robotic manipulator system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

  1. Rocco, P.: Stability of PID control for industrial robot arms. IEEE Trans. Robot. Autom. 12(2), 606–614 (1996)

    MATH  Google Scholar 

  2. Sha, Y., Hu, J., Yao, J.: Active fault-tolerant control strategy for electromechanical servo system based on dual fuzzy RBF neural networks and velocity reconstruction. Int. J. Fuzzy Syst. 25, 715–730 (2023)

    MATH  Google Scholar 

  3. Kim, E.: Output feedback tracking control of robot manipulators with model uncertainty via adaptive fuzzy logic. IEEE Trans. Fuzzy Syst. 12(3), 368–378 (2004)

    MATH  Google Scholar 

  4. Zhang, L., Che, W., Wu, Z.: Prescribed performance control for multiagent systems via fuzzy adaptive event-triggered strategy. IEEE Trans. Fuzzy Syst. 30(12), 5078–5090 (2022)

    MATH  Google Scholar 

  5. Slotine, J., Sastry, S.: Tracking control of non-linear systems using sliding surfaces, with application to robot manipulators. Int. J. Control 38(2), 465–492 (1983)

    MATH  Google Scholar 

  6. Zheng, M., Su, Y., Yang, S., Li, L.: Reliable fuzzy dynamic positioning tracking controller for unmanned surface vehicles based on aperiodic measurement information. Int. J. Fuzzy Syst. 25, 358–368 (2023)

    MATH  Google Scholar 

  7. Utkin, V., Guldner, J., Shi, J.: Sliding mode control in electro-mechanical systems, 2nd edn. CRC Press, Boca Raton (2017)

    MATH  Google Scholar 

  8. Obeid, H., Laghrouche, S., Fridman, L.: Dual layer barrier functions based adaptive higher order sliding mode control. Int. J. Robust Nonlinear Control. 31(9), 3795–3808 (2021)

    MathSciNet  MATH  Google Scholar 

  9. Zhai, J., Li, Z.: Fast-exponential sliding mode control of robotic manipulator with super-twisting method. IEEE Trans. Circ. Syst. II. 69(2), 489–493 (2022)

    MATH  Google Scholar 

  10. Yi, S., Zhai, J.: Adaptive second-order fast nonsingular terminal sliding mode control for robotic manipulators. ISA Trans. 90, 41–51 (2019)

    MATH  Google Scholar 

  11. Marino, R., Tomei, P.: Adaptive observers with arbitrary exponential rate of convergence for nonlinear systems. IEEE Trans. Autom. Control 40(7), 1300–1304 (1995)

    MathSciNet  MATH  Google Scholar 

  12. Parra-Vega, V., Castillo-Tapia, A., Arteaga-Prez, M.A.: Regressorfree second order sliding mode control for exponential tracking of constrained robot manipulators. In: Proceedings of the third international workshop on robot motion and control, Bukowy Dworek, Poland, pp. 159–164 (2002)

  13. Tang, Y.: Terminal sliding mode control for rigid robots. Automatica 34(1), 51–56 (1998)

    MathSciNet  MATH  Google Scholar 

  14. Man, Z., Paplinski, A., Wu, H.: A robust MIMO terminal sliding mode control scheme for rigid robotic manipulators. IEEE Trans. Autom. Control 39(12), 2464–2469 (1994)

    MathSciNet  MATH  Google Scholar 

  15. Yu, S., Yu, X., Shirinzadeh, B., Man, Z.: Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 41(11), 1957–1964 (2005)

    MathSciNet  MATH  Google Scholar 

  16. Wang, L., Chai, T., Zhai, L.: Neural-network-based terminal sliding-mode control of robotic manipulators including actuator dynamics. IEEE Trans. Ind. Electron. 56(9), 3296–3304 (2009)

    MATH  Google Scholar 

  17. Lu, K., Xia, Y.L.: Adaptive attitude tracking control for rigid spacecraft with finite-time convergence. Automatica 49(12), 3591–3599 (2013)

    MathSciNet  MATH  Google Scholar 

  18. Zhai, J., Xu, G.: A novel non-singular terminal sliding mode trajectory tracking control for robotic manipulators. IEEE Trans. Circ. Syst. II. 68(1), 391–395 (2021)

    MATH  Google Scholar 

  19. Rubio, J.J.: Sliding mode control of robotic arms with deadzone. IET Control Theory Appl. 11(8), 1214–1221 (2017)

    MathSciNet  MATH  Google Scholar 

  20. Ma, H., Li, Y.: A novel dead zone reaching law of discrete-time sliding mode control with disturbance compensation. IEEE Trans. Ind. Electron. 67(6), 4815–4825 (2020)

    MATH  Google Scholar 

  21. Zhou, X., Wang, H., Tian, Y., Zheng, G.: Disturbance observer-based adaptive boundary iterative learning control for a rigid-flexible manipulator with input backlash and endpoint constraint. Int. J. Adapt. Control Signal Process. 34(9), 1220–1241 (2020)

    MathSciNet  MATH  Google Scholar 

  22. Sun, G., Zhao, J., Chen, Q.: Observer-based compensation control of servo systems with backlash. Asian J. Control 23(1), 499–512 (2021)

    MathSciNet  MATH  Google Scholar 

  23. Levant, A.: Sliding order and sliding accuracy in sliding mode control. Int. J. Control 58(6), 1247–1263 (1993)

    MathSciNet  MATH  Google Scholar 

  24. Chalanga, A., Kamal, S., Fridman, L., Bandyopadhyay, B., Moreno, J.: Implementation of super-twisting control: super-twisting and higher order sliding-mode observer-based approaches. IEEE Trans. Ind. Electron. 63(6), 3677–3685 (2016)

    MATH  Google Scholar 

  25. Van, M., Ge, S.S., Ren, H.: Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans. Cybern. 47(7), 1681–1693 (2017)

    MATH  Google Scholar 

  26. Li, Z., Zhai, J., Karimi, H.R.: Adaptive finite-time super-twisting sliding mode control for robotic manipulators with control backlash. Int. J. Robust Nonlinear Control 31(17), 8537–8550 (2021)

    MathSciNet  MATH  Google Scholar 

  27. Van, M., Ge, S.: Adaptive Fuzzy integral sliding-mode control for robust fault-tolerant control of robot manipulators with disturbance observer. IEEE Trans. Fuzzy Syst. 29(5), 1284–1296 (2021)

    MATH  Google Scholar 

  28. Zhai, D., An, L., Li, J., Zhang, Q.: Adaptive fuzzy fault-tolerant control with guaranteed tracking performance for nonlinear strict-feedback systems. Fuzzy Set Syst. 302, 82–100 (2016)

    MathSciNet  MATH  Google Scholar 

  29. Chang, Y., Chen, B.: Robust tracking designs for both holonomic and nonholonomic constrained mechanical systems: adaptive fuzzy approach. IEEE Trans. Fuzzy Syst. 8(1), 46–66 (2000)

    MATH  Google Scholar 

  30. Wang, Y., Jiang, B., Wu, Z., Xie, S., Peng, Y.: Adaptive sliding mode fault-tolerant fuzzy tracking control with application to unmanned marine vehicles. IEEE Trans. Syst. Man Cybern. Syst. 51(11), 6691–6700 (2021)

    MATH  Google Scholar 

  31. Utkin, V., Poznyak, A.: Adaptive sliding mode control with application to super-twist algorithm: equivalent control method. Automatica 49(1), 39–47 (2013)

    MathSciNet  MATH  Google Scholar 

  32. Mobayen, S.: An adaptive fast terminal sliding mode control combined with global sliding mode scheme for tracking control of uncertain nonlinear third-order systems. Nonlinear Dyn. 82, 599–610 (2015)

    MathSciNet  MATH  Google Scholar 

  33. Zhu, L., Che, W.: Dynamic event-triggered model-free adaptive security tracking control for constrained subway train system. Int. J. Robust Nonlinear Control 33(3), 2304–2319 (2023)

    MathSciNet  MATH  Google Scholar 

  34. Shao, K., Zheng, J., Huang, K., Wang, H., Man, Z., Fu, M.: Finite-time control of a linear motor positioner using adaptive recursive terminal sliding mode. IEEE Trans. Ind. Electron. 67(8), 6659–6668 (2020)

    MATH  Google Scholar 

  35. Shao, K., Tang, R., Xu, F., Wang, X., Zheng, J.: Adaptive sliding mode control for uncertain Euler-Lagrange systems with input saturation. J. Frankl. Inst. 358, 8356–8376 (2021)

    MathSciNet  MATH  Google Scholar 

  36. Shtessel, Y., Taleb, M., Plestan, F.: A novel adaptive-gain super twisting sliding mode controller: methodology and application. Automatica 48(5), 759–769 (2012)

    MathSciNet  MATH  Google Scholar 

  37. Boukattaya, M., Mezghani, N., Damak, T.: Adaptive nonsingular fast terminal sliding-mode control for the tracking problem of uncertain dynamical systems. ISA Trans. 77, 1–19 (2018)

    MATH  Google Scholar 

  38. Mondal, S., Mahanta, C.: Adaptive second order terminal sliding mode controller for robotic manipulators. J. Frankl. Inst. 351(4), 2356–2377 (2014)

    MathSciNet  MATH  Google Scholar 

  39. Mobayen, S., Tchier, F., Ragoub, L.: Design of an adaptive tracker for n-link rigid robotic manipulators based on super-twisting global nonlinear sliding mode control. Int. J. Syst. Sci. 48(9), 1990–2002 (2017)

    MathSciNet  MATH  Google Scholar 

  40. He, S., Lin, D., Wang, J.: Chattering-free adaptive fast convergent terminal sliding mode controllers for position tracking of robotic manipulators. Proc. Inst. Mech. Eng. C 230(4), 514–526 (2016)

    MATH  Google Scholar 

  41. Yang, B., Lin, W.: Homogeneous observers, iterative design, and global stabilization of high-order nonlinear systems by smooth output feedback. IEEE Trans. Autom. Control 49(7), 1069–1080 (2004)

    MathSciNet  MATH  Google Scholar 

  42. Bhat, S., Bernstein, D.: Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 38(3), 751–766 (2000)

    MathSciNet  MATH  Google Scholar 

  43. Feng, Y., Yu, X., Man, Z.: Non-singular terminal sliding mode control of rigid manipulators. Automatica 38(12), 2159–2167 (2002)

    MathSciNet  MATH  Google Scholar 

  44. Zhu, W.: Comments on “Robust tracking control for rigid robotic manipulators’’. IEEE Trans. Autom. Control 45(8), 1577–1580 (2000)

    MATH  Google Scholar 

Download references

Acknowledgements

This work is supported in part by the Natural Science Foundation of Jiangsu Province (BK20211162) and the National Natural Science Foundation of China (61873061).

Author information

Authors and Affiliations

  1. School of Automation, Southeast University, Nanjing, 210096, Jiangsu, China

    Zeyu Li & Junyong Zhai

Authors
  1. Zeyu Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Junyong Zhai
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Junyong Zhai.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Z., Zhai, J. Fuzzy Adaptive Super-Twisting Sliding Mode Asymptotic Tracking Control of Robotic Manipulators. Int. J. Fuzzy Syst. 26, 34–43 (2024). https://doi.org/10.1007/s40815-023-01573-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-023-01573-3

Keywords