Skip to main content

Advertisement

Springer Nature Link
Log in

Interval Type-2 Fuzzy Set-Theoretic Control Design for Uncertain Dynamical Systems

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

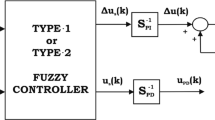
Fuzzy set plays an important role in handling vagueness for controlling uncertain dynamical systems. However, conventional type-1 fuzzy set (T1FS) requires precisely defined membership function, which is usually unavailable in practical control applications. This study pioneers the use of IT2FS for the control design of uncertain dynamical systems to relax this limitation of conventional T1FS-based control design. Concretely, the considered (possibly fast) time-variant uncertainty is bounded with the bound lying within IT2FS (hence interval type-2 fuzzy dynamical system, IT2FDS). A robust control design approach is proposed without invoking any IF-THEN fuzzy rules, providing a two-layer performance. The lower layer renders uniform boundedness and uniform ultimate boundedness for the system by the Lyapunov analysis, ensuring the bottom line. The upper layer improves the fuzzy-based control performance by optimal gain design oriented by a two-player zero-sum game, taking advantage of the interval description of membership function. It is shown that the equilibrium of the game which contains the optimal gain always exists. A semi-analytical solution strategy for the equilibrium is given. This is the first endeavor in exploring IT2FS-based control design without using any IF-THEN rules. It is shown in the demonstrative examples that the proposed IT2FS-based approach can achieve better control performance than the conventional T1FS-based approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

Not applicable.

References

  1. Petersen, I., Tempo, R.: Robust control of uncertain systems: classical results and recent developments. Automatica 50(5), 1315–1335 (2014)

    MathSciNet  Google Scholar 

  2. Derrouaoui, S.H., Bouzid, Y., Guiatni, M.: Nonlinear robust control of a new reconfigurable unmanned aerial vehicle. Robotics 10(2), 76 (2021)

    Google Scholar 

  3. Durrett, R.: Probability. Cambridge University Press, Leiden (2010)

    Google Scholar 

  4. Kushner, H.: On the stability of stochastic dynamical systems. Proc. Natl. Acad. Sci. U.S.A. 53(1), 8–12 (1965)

    MathSciNet  Google Scholar 

  5. Clark, A.: Control barrier functions for stochastic systems. Automatica 130, 109688 (2021)

    MathSciNet  Google Scholar 

  6. Li, Y., Zhang, J., Liu, W., et al.: Observer-based adaptive optimized control for stochastic nonlinear systems with input and state constraints. IEEE Trans. Neural Netw. Learn. Syst. 33(12), 7791–7805 (2021)

    MathSciNet  Google Scholar 

  7. Pincus, S., Kalman, R.E.: Not all (possibly) ‘random’ sequences are created equal. Proc. Natl. Acad. Sci. U.S.A. 94, 3513–3518 (1997)

    MathSciNet  Google Scholar 

  8. Xia, B., Yu, D.: Interval analysis of acoustic field with uncertain-but-bounded parameters. Comput. Struct. 112, 235–244 (2012)

    Google Scholar 

  9. Adhikari, S., Khodaparast, H.H.: A spectral approach for fuzzy uncertainty propagation in finite element analysis. Fuzzy Sets Syst. 243, 1–24 (2014)

    MathSciNet  Google Scholar 

  10. Zadeh, L.A.: Fuzzy sets. Inf. Control 8(3), 338–353 (1965)

    Google Scholar 

  11. Zadeh, L.A.: Fuzzy logic. In: Granular, Fuzzy, and Soft Computing, pp. 19–49. Springer, New York (2023)

  12. Yin, H., Yu, D., Yin, S., Xia, B.: Possibility-based robust design optimization for the structural-acoustic system with fuzzy parameters. Mech. Syst. Signal Process. 102, 329–345 (2018)

    Google Scholar 

  13. Khan, M.J., Kumam, P., Deebani, W., et al.: Bi-parametric distance and similarity measures of picture fuzzy sets and their applications in medical diagnosis. Egypt. Inform. J. 22(2), 201–212 (2021)

    Google Scholar 

  14. Stekelorum, R., Laguir, I., Gupta, S., et al.: Green supply chain management practices and third-party logistics providers’ performances: a fuzzy-set approach. Int. J. Prod. Econ. 235, 108093 (2021)

    Google Scholar 

  15. Zhang, H., Zheng, J., Feng, L.: Command filter-based adaptive fuzzy tracking control of stochastic robotic systems with full state constraints. Int. J. Fuzzy Syst. (2023). https://doi.org/10.1007/s40815-023-01535-9

    Article  Google Scholar 

  16. Mhawesh, M.A., Kashkool, A.S.: Controlling the half-step mode operation of the variable reluctance stepper motor by using Mamdani type of fuzzy logic controller. Int. J. Electr. Comput. Eng. 12(6), 5950 (2022)

    Google Scholar 

  17. Li, H., Song, B., Tang, X., et al.: Adaptive pareto optimal control of T-S fuzzy system with input constraints and its application. Int. J. Fuzzy Syst. (2022). https://doi.org/10.1007/s40815-021-01180-0

    Article  Google Scholar 

  18. Chen, Y.H.: A new approach to the control design of fuzzy dynamical systems. J. Dyn. Syst. Meas. Control 133(6), 061019 (2011)

    Google Scholar 

  19. Xu, J., Chen, Y.H., Guo, H.: On the foundations of fuzzy dynamical system theory: controllability and observability. Int. J. Fuzzy Syst. 16(4), 497–510 (2014)

    MathSciNet  Google Scholar 

  20. Yin, H., Chen, Y.H., Yu, D.: Stackelberg-theoretic approach for performance improvement in fuzzy systems. IEEE Trans. Cybernetics 50(5), 2223–2236 (2020)

    Google Scholar 

  21. Sun, Q., Yang, G., Wang, X., Chen, Y.H.: Regulating constraint-following bound for fuzzy mechanical systems: indirect robust control and fuzzy optimal design. IEEE Trans. Cybernetics 52(7), 5868–5881 (2022)

    Google Scholar 

  22. Dong, F., Zhao, X., Chen, Y.H.: Optimal longitudinal control for vehicular platoon systems: adaptiveness, determinacy, and fuzzy. IEEE Trans. Fuzzy Syst. 29(4), 889–903 (2021)

    Google Scholar 

  23. Yang, Z., Huang, J., Yang, D., Zhong, Z.: Design and optimization of robust path tracking control for autonomous vehicles with fuzzy uncertainty. IEEE Trans. Fuzzy Syst. 30(6), 1788–1800 (2022)

    Google Scholar 

  24. Li, C., Zhao, H., Zhen, S., Chen, Y.H.: Control design with optimization for fuzzy steering-by-wire system based on Nash game theory. IEEE Trans. Cybernetics 52(8), 7694–7703 (2022)

    Google Scholar 

  25. Hui, Z., Huang, J., Yan, Z., et al.: Cooperative-game-oriented optimal design in vehicle lateral stability control with fuzzy uncertainties. Int. J. Fuzzy Syst. (2022). https://doi.org/10.1007/s40815-021-01160-4

    Article  Google Scholar 

  26. Mendel, J.M.: Uncertain Rule-Based Fuzzy Systems: Introduction and New Directions. Springer, Berlin (2017)

    Google Scholar 

  27. Zadeh, L.A.: The concept of a linguistic variable and its application to approximate reasoning-1. Inf. Sci. 8, 199–249 (1975)

    MathSciNet  Google Scholar 

  28. De, A.K., Chakraborty, D., Biswas, A.: Literature review on type-2 fuzzy set theory. Soft Comput. 26(18), 9049–9068 (2022)

    Google Scholar 

  29. Liang, Q., Mendel, J.: Interval type-2 fuzzy logic systems: theory and design. IEEE Trans. Fuzzy Syst. 8, 535–550 (2000)

    Google Scholar 

  30. Wu, D., Mendel, J.M.: Uncertainty measures for interval type-2 fuzzy sets. Inf. Sci. 177(23), 5378–5393 (2007)

    MathSciNet  Google Scholar 

  31. Wu, D.: A brief Tutorial on Interval type-2 fuzzy sets and systems. Fuzzy Sets Syst. 4(1), 220–225 (2010)

    Google Scholar 

  32. Sola, H.B., Fernandez, J., Hagras, H., Herrera, F., Pagola, M., Barrenechea, E.: Interval type-2 fuzzy sets are generalization of interval-valued fuzzy sets: toward a wider view on their relationship. IEEE Trans. Fuzzy Syst. 23(5), 1876–1882 (2014)

    Google Scholar 

  33. Jankova, Z., Jana, D.K., Dostal, P.: Investment decision support based on interval type-2 fuzzy expert system. Eng. Econ. 32(2), 118–129 (2021)

    Google Scholar 

  34. Paul, S., Turnbull, R., Khodadad, D., et al.: A vibration based automatic fault detection scheme for drilling process using type-2 fuzzy logic. Algorithms 15(8), 284 (2021)

    Google Scholar 

  35. Zhang, Q., Wang, Y., Cheng, J., et al.: Improved filtering of interval type-2 fuzzy systems over Gilbert-Elliott channels. Inf. Sci. 627, 132–146 (2023)

    Google Scholar 

  36. Mendel, J.M., John, R.I., Liu, F.: Interval type-2 fuzzy logic systems made simple. IEEE Trans. Fuzzy Syst. 14(6), 808–821 (2006)

    Google Scholar 

  37. Chen, C., Huang, J., Wu, D., et al.: Interval type-2 fuzzy disturbance observer-based T-S fuzzy control for a pneumatic flexible joint. IEEE Trans. Ind. Electron. 69(6), 5962–5972 (2021)

    Google Scholar 

  38. Lian, Z., Shi, P., Lim, C.C.: Hybrid-triggered interval type-2 fuzzy control for networked systems under attacks. Inf. Sci. 567, 332–347 (2021)

    MathSciNet  Google Scholar 

  39. Tao, X., Yi, J., Pu, Z., Xiong, T.: Robust adaptive tracking control for hypersonic vehicle based on interval type-2 fuzzy logic system and small-gain approach. IEEE Trans. Cybernetics 51(5), 2504–2517 (2021)

    Google Scholar 

  40. Chen, C., Huang, J., Wu, D., Tu, X.: Interval type-2 fuzzy disturbance observer-based T-S fuzzy control for a pneumatic flexible joint. IEEE Trans. Ind. Electron. 69(6), 5962–5972 (2021)

    Google Scholar 

  41. Sun, X., Zhang, Q.: Admissibility analysis for interval type-2 fuzzy descriptor systems based on sliding mode control. IEEE Trans. Cybernetics 49(8), 3032–3040 (2019)

    Google Scholar 

  42. Leitmann, G.: Cooperative and Non-cooperative Many Players Differential Games. Springer, Vienna (1974)

    Google Scholar 

  43. Chen, Y.H., Leitmann, G.: Robustness of uncertain systems in the absence of matching assumptions. Int. J. Control 45(5), 1527–1542 (1987)

    MathSciNet  Google Scholar 

  44. Nash, J.: Equilibrium points in \(n\)-person games. Proc. Natl. Acad. Sci. U.S.A. 36(1), 48–49 (1950)

    MathSciNet  Google Scholar 

  45. Brookfield, G.: Factoring quartic polynomials: a lost art. Math. Mag. 80(1), 67–70 (2007)

    Google Scholar 

  46. Nocedal, J., Wright, S.J.: Numerical Optimization, 2nd edn. Springer, New York (2006)

    Google Scholar 

  47. Erbatur, K., Kurt, O.: Natural ZMP trajectories for biped robot reference generation. IEEE Trans. Ind. Electron. 56(3), 835–845 (2009)

    Google Scholar 

  48. Nah, J., Yim, S.: Vehicle stability control with four-wheel independent braking, drive and steering on in-wheel motor-driven electric vehicles. Electronics 9(11), 1934 (2020)

    Google Scholar 

Download references

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 52105096, 52175087), in part by the GuangDong Basic and Applied Basic Research Foundations, China (Grant No. 2021A1515011752), in part by the the Fundamental Research Funds for the Central Universities (No. 531110810651), in part by the Natural Science Foundation of Hunan Province of China (Grant No. 2022JJ40084), and in part by the Scientific Research Project of the Education Department of Hunan Province of China (No. 21B0029).

Author information

Authors and Affiliations

  1. College of Mechanical and Vehicle Engineering, Hunan University, Changsha, 410082, Hunan, People’s Republic of China

    Yifan Liu, Hui Yin, Baizhan Xia & Dejie Yu

  2. The George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA, 30332, USA

    Ye-Hwa Chen

Authors
  1. Yifan Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hui Yin
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Baizhan Xia
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Dejie Yu
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Ye-Hwa Chen
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Hui Yin.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Y., Yin, H., Xia, B. et al. Interval Type-2 Fuzzy Set-Theoretic Control Design for Uncertain Dynamical Systems. Int. J. Fuzzy Syst. 26, 1069–1087 (2024). https://doi.org/10.1007/s40815-023-01654-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-023-01654-3

Keywords