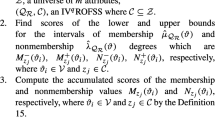Abstract
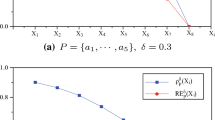
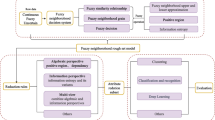
Type-2 fuzzy information systems (TFISs-2), one interesting form of complex data, are extensions of fuzzy information systems. Uncertainty measurement and attribute reduction of TFISs-2 are key issues when describing and analyzing complex fuzzy data. However, existing researches mainly focus on the traditional fuzzy data, and seldom consider type-2 fuzzy data. This paper focuses on finding an effective indicator to measure the uncertainty of TFISs-2, and carries out the research of attribute reduction based on this indicator. Firstly, the weighted membership distance and the weighted membership similarity are defined, which are used to describe the relation between two objects in TIFSs-2, and \(\sigma \) similarity relations are introduced. Secondly, a fuzzy neighborhood structure is defined based on \(\sigma \) similarity relations. The classical rough set model is extended on TFISs-2, and the definitions of upper and lower approximation, accuracy and roughness are given. Then, a novel indicator called \(\sigma \) self-information is used to describe the uncertainty of TFISs-2, and a heuristic greedy selection attribute reduction algorithm is proposed. Finally, the experimental results show that the constructed uncertainty measurement indicator is suitable for TFISs-2, and the proposed attribute reduction method is effective. This study is beneficial to promote the understanding of complex fuzzy data, and contributes to the data analysis and processing of TFISs-2.









Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data availability
The authors confirm that the data used in this study are available within the paper.
References
Pawlak, Z.: Rough sets. Int. J. Comput. Inf. Sci. 11(5), 341–356 (1982)
Pawlak, Z.: Rough Sets: Theoretical Aspects of Reasoning About Data. Springer, New York (1991)
Dai, J., Xu, Q.: Attribute selection based on information gain ratio in fuzzy rough set theory with application to tumor classification. Appl. Soft Comput. 13(1), 211–221 (2013)
Liang, J., Feng, W., Dang, C., et al.: A Group incremental approach to feature selection applying rough set Technique. IEEE Trans. Knowl. Data Eng. 26(2), 294–308 (2014)
Dai, J., Han, H., Hu, Q., et al.: Discrete particle swarm optimization approach for cost sensitive attribute reduction. Knowl.-Based Syst. 102(15), 116–126 (2016)
Dai, J., Han, H., Zhang, X., et al.: Catoptrical rough set model on two universes using granule-based definition and its variable precision extensions. Inf. Sci. 390, 70–81 (2017)
Dai, J., Hu, Q., Hu, H., et al.: Neighbor inconsistent pair selection for attribute reduction by rough set approach. IEEE Trans. Fuzzy Syst. 26(2), 937–950 (2018)
Zadeh, L.A.: Fuzzy sets. Inf. Control 8(3), 338–353 (1965)
Zadeh, L.A.: The concept of a linguistic variable and its application to approximate reasoning. Inf. Sci. 8(3), 199–249 (1974)
Mendel, J.M.: Ieee transactions on fuzzy systems special issue on advances in type-2 fuzzy sets and systems. IEEE Comput. Intell. Mag. 7(1), 75–75 (2007)
Ruiz, G., Hagras, H., Pomares, H., et al.: Join and meet operations for type-2 fuzzy sets with non-convex secondary memberships. IEEE Trans. Fuzzy Syst. 24(4), 1000–1008 (2016)
Mendel, J.M.: Type-2 fuzzy sets as well as computing with words. IEEE Comput. Intell. Mag. 14(1), 82–95 (2019)
Karnik, N.N., Mendel, J.M., Liang, Q.: Type-2 fuzzy logic systems. IEEE Trans. Fuzzy Syst. 7(6), 643–658 (1999)
Carter, J., Mendel, J., John, R., et al.: The extended sup-star composition for type-2 fuzzy sets made simple. In: IEEE International Conference on Fuzzy Systems. IEEE, pp. 1441–1445 (2006)
Zhai, D., Mendel, J.M.: Uncertainty measures for general Type-2 fuzzy sets. Inf. Sci. 181(3), 503–518 (2009)
Wagner, C., Miller, S., Garibaldi, J.M., et al.: From interval-valued data to general type-2 fuzzy sets. IEEE Trans. Fuzzy Syst. 23(2), 248–269 (2015)
Mendel, J.M., Rajati, M.R., Sussner, P.: On clarifying some definitions and notations used for type-2 fuzzy sets as well as some recommended changes. Inf. Sci. 340, 337–345 (2016)
Almohammadi, K.: Type-2 fuzzy logic based systems for adaptive learning and teaching within intelligent e-learning environments. University of Essex (2016)
Runkler, T., Coupland, S., John, R.: Interval type-2 fuzzy decision making. Int. J. Approx. Reason. 80, 217–224 (2017)
Castillo, O., Amador-Angulo, L.: A generalized type-2 fuzzy logic approach for dynamic parameter adaptation in bee colony optimization applied to fuzzy controller design. Inf. Sci. 460, 476–496 (2018)
Li, J., John, R., Coupland, S., et al.: On Nie-Tan operator and type-reduction of interval type-2 fuzzy Sets. IEEE Trans. Fuzzy Syst. 26(2), 1036–1039 (2018)
Wang, H., Yao, J., Yan, J., et al.: An extended TOPSIS method based on gaussian interval type-2 fuzzy set. Int. J. Fuzzy Syst. 21(6), 1831–1843 (2019)
Wu, D., Mendel, J.M.: Similarity measures for closed general type-2 fuzzy sets: overview, comparisons, and a geometric approach. IEEE Trans. Fuzzy Syst. 27(3), 515–526 (2019)
Yao, Y., Zhao, L.: A measurement theory view on the granularity of partition. Inf. Sci. 213, 1–13 (2012)
Wang, C., Huang, Y., Shao, M., et al.: Uncertainty measures for general fuzzy relations. Fuzzy Sets Syst. 360, 82–96 (2018)
Dai, J., Wang, W., et al.: An Uncertainty measure for incomplete decision tables and its applications. IEEE Trans. Cybernetics 43(4), 1277–1289 (2013)
Dai, J., Wei, B., Zhang, X., et al.: Uncertainty measurement for incomplete interval-valued information systems based on \(\alpha \)-weak similarity. Knowl.-Based Syst. 136, 159–171 (2017)
Liu, X., Li, Z., Zhang, G., et al.: Measures of uncertainty for a distributed fully fuzzy information system. Int. J. Gen. Syst. 48(6), 625–655 (2019)
Su, Z., Xu, Z., Zhao, H., et al.: Entropy measures for probabilistic hesitant fuzzy information. IEEE Access 7, 65714–65727 (2019)
Li, Z., Liu, X., Dai, J., et al.: Measures of uncertainty based on Gaussian kernel for a fully fuzzy information system. Knowl.-Based Syst. 196, 105791 (2020)
Yang, X., Yong, Q., Yu, D.J., et al.: \(\alpha \)-Dominance relation and rough sets in interval-valued information systems. Inf. Sci. 294(5), 334–347 (2015)
Dai, J., Yan, Y., Li, Z., et al.: Dominance-based fuzzy rough set approach for incomplete interval-valued data. J. Intell. Fuzzy Syst. 34(1), 423–436 (2018)
Zhao, H., Qin, K.: Mixed feature selection in incomplete decision table. Knowl.-Based Syst. 57, 181–190 (2014)
Dai, J., Hu, H., Zheng, G.J., et al.: Attribute reduction in interval-valued information systems based on information entropies. Front. Inf. Technol. Electron. Eng. 17(9), 919–928 (2016)
Thuy, N.N., Wongthanavasu, S.: On reduction of attributes in inconsistent decision tables based on information entropies and stripped quotient sets. Expert Syst. Appl. 137, 308–323 (2019)
Sun, L., Yin, T., Ding, W., et al.: Multilabel feature selection using ML-ReliefF and neighborhood mutual information for multilabel neighborhood decision systems. Inf. Sci. 537, 401–424 (2020)
Dubois, D., Prade, H.: Rough fuzzy sets and fuzzy rough sets. Int. J. Gen. Syst. 17(2–3), 191–209 (2007)
Sun, B., Ma, W., Chen, X.: Fuzzy rough set on probabilistic approximation space over two universes and its application to emergency decision-making. Expert Syst. 32(4), 507–521 (2015)
Dai, J., Xu, Q.: Attribute selection based on information gain ratio in fuzzy rough set theory with application to tumor classification. Appl. Soft Comput. J. 13(1), 211–221 (2013)
Dai, J., Hu, H., Wu, W.Z., et al.: Maximal-discernibility-pair-based approach to attribute reduction in fuzzy rough sets. IEEE Trans. Fuzzy Syst. 26(4), 2174–2187 (2018)
Yang, Y., Chen, D., Hui, W.: Incremental perspective for feature selection based on fuzzy rough sets. IEEE Trans. Fuzzy Syst. 26(3), 1257–1273 (2018)
Yao, Y., Zhao, Y., Wang, J.: On reduct construction algorithms. Trans. Comput. Sci. II, 100–117 (2008)
Ni, P., Zhao, S., Wang, X., et al.: PARA: A positive-region based attribute reduction accelerator. Information Sciences, 503(C) (2019)
Wang, C., Qi, Y., Shao, M., et al.: A fitting model for feature selection with fuzzy rough sets. IEEE Trans. Fuzzy Syst. 25(4), 741–753 (2017)
Wang, C., Huang, Y., Shao, M., et al.: feature selection based on neighborhood self-information. IEEE Trans. Cybernetics 50(9), 4031–4042 (2019)
Liu, X., Dai, J., Chen, J., et al.: Measures of uncertainty based on gaussian kernel for type-2 fuzzy information systems. Int. J. Fuzzy Syst. 23(4), 1163–1178 (2021)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (62376093, 61976089, 61473259), the Major Program of the National Social Science Foundation of China (20&ZD047), the Humanities and Social Sciences Research of Ministry of Education of China (19YJAZH069), the Natural Science Foundation of Hunan Province (2021JJ30451, 2022JJ30397), the Hunan Provincial Science & Technology Project Foundation (2018RS3065, 2018TP1018), and the Postgraduate Scientific Research Innovation Project of Hunan Province, China (QL20230131).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Qi, Z., Zhan, L., Dai, J. et al. Attribute Reduction of Type-2 Fuzzy Information Systems Based on \(\sigma \) Self-information. Int. J. Fuzzy Syst. 26, 1428–1447 (2024). https://doi.org/10.1007/s40815-024-01677-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-024-01677-4