Skip to main content

Advertisement

Springer Nature Link
Log in

Practical Finite-Time Synchronization of T-S Fuzzy Complex Networks with Different Couplings via Semi-intermittent Control

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

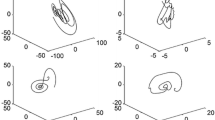
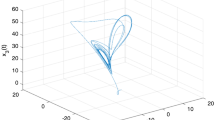
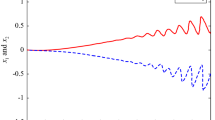
Based on Takagi-Sugeno(T-S) fuzzy models, this paper investigates practical finite-time(PFET) synchronization of complex networks with a linear coupling and two different kinds of nonlinear couplings, including nonlinear relative state coupling and nonlinear absolute state coupling. A new stability lemma is established based on different time intervals. Two kinds of controllers are designed including semi-intermittent state feedback control and semi-intermittent adaptive control. As a result, with the help of new stability lemma and control schemes, the goal of PFET synchronization is realized via Lyapunov functionals. Eventually, simulation experiments are presented to verify our new results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

Data sharing is not applicable to this article, as no datasets were generated or analyzed during the current study.

References

  1. Takagi, T., Sugeno, M.: Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 15(1), 116–132 (1985)

    Article  MATH  Google Scholar 

  2. Divya, H., Sakthivel, R., Liu, Y., Sakthivel, R.: Delay-dependent synchronization of T-S fuzzy Markovian jump complex dynamical networks. Fuzzy Sets Syst. 416, 108–124 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  3. Wei, B., Xiao, F., Shi, Y.: Fully distributed synchronization of dynamic networked systems with adaptive nonlinear couplings. IEEE Trans. Cybern. 50(7), 2926–2934 (2020)

    Article  MATH  Google Scholar 

  4. Xu, Y., Sun, J., Wang, G., Wu, Z.G.: Dynamic triggering mechanisms for distributed adaptive synchronization control and its application to circuit systems. IEEE Trans. Circuits Syst. I Regul. Papers 68(5), 2246–2256 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  5. Feng, J., Xie, J., Wang, J., Zhao, Y.: Secure synchronization of stochastic complex networks subject to deception attack with nonidentical nodes and internal disturbance. Inf. Sci. 547, 514–525 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  6. Ren, Y., Jiang, H., Li, J., Lu, B.: Finite-time synchronization of stochastic complex networks with random coupling delay via quantized aperiodically intermittent control. Neurocomputing 420, 337–348 (2021)

    Article  MATH  Google Scholar 

  7. Cai, X., Shi, K., She, K., Zhong, S., Wang, J., Yan, H.: New results for T-S fuzzy systems with hybrid communication delays. Fuzzy Sets Syst. 438, 1–24 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  8. Haimo, V.T.: Finite time controllers. SIAM J. Control. Optim. 24(4), 760–770 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  9. Bowong, S., Kakmeni, F.M.M.: Chaos control and duration time of a class of uncertain chaotic systems. Phys. Lett. A 316, 206–217 (2003)

    Article  MATH  Google Scholar 

  10. Yang, X., Cao, J.: Finite-time stochastic synchronization of complex networks. Appl. Math. Model. 34, 3631–3641 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  11. Benabdallah, A., Ellouze, I., Hammami, M.A.: Practical stablity of nonlinear time-varying cascades systems. J. Dyn. Control Syst. 15(1), 45–62 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Hamed, B.B., Hammami, M.A.: Practical stabilization of a class of uncertain time-varying nonlinear delay systems. J. Control Theory Appl. 7(2), 175–180 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  13. Zhai, S., Li, Q.: Practical bipartite synchronization via pinning control on a network of nonlinear agents with antagonistic interactions. Nonlinear Dyn. 87, 207–218 (2017)

    Article  MATH  Google Scholar 

  14. Sun, W., Lv, X.: Practical finite-time fuzzy control for Hamiltonian systems via adaptive event-triggered approach. Int. J. Fuzzy Syst. 22(1), 35–45 (2020)

    Article  MATH  Google Scholar 

  15. Louodop, P., Kountchou, M., Fotsin, H., Bowong, S.: Practical finite-time synchronization of jerk systems: theory and experiment. Nonlinear Dyn. 78, 597–607 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  16. Ning, B., Han, Q.L., Zuo, Z.: Practical fixed-time consensus for integrator-type multi-agent systems: a time base generator approach. Automatica 105, 406–414 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  17. Gong, P., Han, Q.L.: Practical fixed-time bipartite consensus of nonlinear incommensurate fractional-order multiagent systems in directed signed networks. SIAM J. Control. Optim. 58(6), 3322–3341 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  18. Diao, S., Sun, W., Wang, L., Wu, J.: Finite-time adaptive fuzzy control for nonlinear systems with unknown backlash-like hysteresis. Int. J. Fuzzy Syst. 23(7), 2037–2047 (2021)

    Article  MATH  Google Scholar 

  19. Wang, W., Hu, J., Mei, J., Wang, S.: Finite time adaptive neural intermittent control for a class of nonlinear dynamical systems. 1–24 (2022). https://doi.org/10.21203/rs.3.rs-2496525/v1

  20. Zhou, Y., Wan, X., Huang, C., Yang, X.: Finite-time stochastic synchronization of dynamic networks with nonlinear coupling strength via quantized intermittent control. Appl. Math. Comput. 376, 125157 (2020)

    MathSciNet  MATH  Google Scholar 

  21. Xu, D., Song, S., Su, H.: Fixed-time synchronization of large-scale systems via aperiodically intermittent control. Chaos Solitons Fractals 173, 113613 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  22. Tang, R., Yang, X., Shi, P., Xiang, Z., Qing, L.: Finite-time \(\cal{L} _{2}\) stabilization of unce$$\cal{L} _{2}$$rtain delayed T-S fuzzy systems via intermittent control. IEEE Trans. Fuzzy Syst. 32(1), 116–125  (2023)

    Article  MATH  Google Scholar 

  23. Xu, C., Yang, X., Lu, J., Feng, J., Alsaadi, F.E., Hayat, T.: Finite-time synchronization of networks via quantized intermittent pinning control. IEEE Trans. Cybern. 48(10), 3021–3027 (2018)

    Article  MATH  Google Scholar 

  24. Gan, Q., Xiao, F., Sheng, H.: Fixed-time outer synchronization of hybrid-coupled delayed complex networks via periodically semi-intermittent control. J. Franklin Inst. 356(12), 6656–6677 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  25. Li, S., Lv, C., Ding, X.: Synchronization of stochastic hybrid coupled systems with multi-weights and mixed delays via aperiodically adaptive intermittent control. Nonlinear Anal. Hybrid Syst. 35, 100819 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  26. Cheng, L., Tang, F., Shi, X., Chen, X., Qiu, J.: Finite-time and fixed-time synchronization of delayed memristive neural networks via adaptive aperiodically intermittent adjustment strategy. IEEE Trans. Neural Netw. Learn. Syst. 34(11), 8516–8530 (2023)

    Article  MathSciNet  Google Scholar 

  27. Liu, J., Ran, G., Wu, Y., Xue, L., Sun, C.: Dynamic event-triggered practical fixed-time consensus for nonlinear multiagent systems. IEEE Trans. Circuits Syst. II: Express Briefs 69(4), 2156–2160 (2022)

    MATH  Google Scholar 

  28. Hardy, G.H., Littlewood, J.E., Pólya, G.: Inequalities. Cambridge University Press, Cambridge (1952)

    MATH  Google Scholar 

Download references

Acknowledgements

This work was jointly supported by the National Natural Science Foundation of China (Grant No. 62003065), Natural Science Foundation of Chongqing, China (Grant No. CSTB2023NSCQ-MSX0771), the Science and Technology Research Program of Chongqing Municipal Education Commission of China (Grant No. KJZD-K202300502).

Author information

Authors and Affiliations

  1. College of Computer and Information Science, Chongqing Normal University, Chongqing, 401331, China

    Li Cao & Wanli Zhang

Authors
  1. Li Cao
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Wanli Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Wanli Zhang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cao, L., Zhang, W. Practical Finite-Time Synchronization of T-S Fuzzy Complex Networks with Different Couplings via Semi-intermittent Control. Int. J. Fuzzy Syst. 26, 1507–1518 (2024). https://doi.org/10.1007/s40815-024-01686-3

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-024-01686-3

Keywords