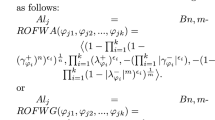Skip to main content

Advertisement

Springer Nature Link
Log in

Some Operators Based on qth Rung Root Orthopair Fuzzy Sets and Their Application in Multi-criteria Decision Making

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

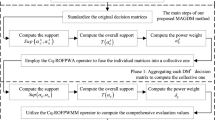
Intuitionistic fuzzy sets have been widely studied and applied as an important means of dealing with information uncertainty. However, the existing intuitionistic fuzzy sets and their extension methods are limited and single in their fuzzy spatial representation of information. Under this environment, this paper proposes a new generalized fuzzy set, called qth Rung Root Orthopair Fuzzy Sets (q-RROFS). Since the q-RROFS can adjust the range of fuzzy space expression by the parameter q, it is superior to intuitionistic fuzzy sets, SR-fuzzy sets, and CR-fuzzy sets. We give some definitions and properties of q-RROFS and give their proofs. Under the q-RROFS, we give its operations and properties and introduce four new weighted aggregation operators, namely, qth Rung Root Orthopair Fuzzy-weighted average operator (q-RROFWA), qth Rung Root Orthopair Fuzzy-weighted geometric operator (q-RROFWG), qth Rung Root Orthopair Fuzzy-weighted power average operator (q-RROFWPA), and qth Rung Root Orthopair Fuzzy-weighted power geometric operator (q-RROFWPG). We discuss the properties of these operators in detail and follow the proof procedure. Then, we give a Multi-criteria decision-making approach under q-RROFS. Finally, we illustrate the effectiveness and applicability of the proposed methodology through practical application examples and comparisons with other methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data availability

The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

References

  1. Zadeh, L.A.: Fuzzy sets. Inf. Control. 8(3), 338–353 (1965)

    Article  MATH  Google Scholar 

  2. Atanassov, K.T.: Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20(1), 87–96 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  3. Cheng, C., et al.: A majority rule-based measure for Atanassov type intuitionistic membership grades in MCDM. IEEE Trans. Fuzzy Syst. 30(1), 121–132 (2020)

    Article  MATH  Google Scholar 

  4. Deb, P.P., et al.: A decision-making model with intuitionistic fuzzy information for selection of enterprise resource planning systems. IEEE Trans. Eng. Manag. 71, 15 (2022)

    MATH  Google Scholar 

  5. Chai, N.J., Zhou, W.L., Jiang, Z.G.: Sustainable supplier selection using an intuitionistic and interval-valued fuzzy MCDM approach based on cumulative prospect theory. Inf. Sci. 626, 710–737 (2023)

    Article  MATH  Google Scholar 

  6. Sharma, K., et al.: Solving a multi-objective chance constrained hierarchical optimization problem under intuitionistic fuzzy environment with its application. Expert Syst. Appl. 217, 16 (2023)

    Article  MATH  Google Scholar 

  7. Rani, D., Ebrahimnejad, A., Gupta, G.: Generalized techniques for solving intuitionistic fuzzy multi-objective non-linear optimization problems. Expert Syst. Appl. 202, 11 (2022)

    Article  MATH  Google Scholar 

  8. Zhao, M., et al.: A telemedicine decision-making model for teleconsultation decision support system based on intuitionistic hesitant fuzzy linguistic term sets. IEEE Trans. Fuzzy Syst. 31(3), 905–918 (2023)

    Article  MATH  Google Scholar 

  9. Khorasani, M., et al.: Evaluating strategies to decarbonize oil and gas supply chain: implications for energy policies in emerging economies. Energy 258, 14 (2022)

    Article  MATH  Google Scholar 

  10. Tiwari, A., Lohani, Q.M.D.: Proposed intuitionistic fuzzy entropy measure along with novel multicriteria sorting techniques. IEEE Access 11, 7630–7656 (2023)

    Article  MATH  Google Scholar 

  11. Yager, R.R.: Pythagorean fuzzy subsets. In: Joint World Congress of the International-Fuzzy-Systems-Association (IFSA)/Annual Meeting of the North-American-Fuzzy-Information-Processing-Society (NAFIPS), 2013. IEEE, Edmonton (2013)

  12. Akram, M., Nawaz, H.S., Kahraman, C.: Rough Pythagorean fuzzy approximations with neighborhood systems and information. Expert Syst. Appl. 218, 14 (2023)

    Article  MATH  Google Scholar 

  13. Pan, L.P., et al.: Constrained Pythagorean fuzzy sets and its similarity measure. IEEE Trans. Fuzzy Syst. 30(4), 1102–1113 (2022)

    Article  MATH  Google Scholar 

  14. Mishra, A.R., et al.: A similarity measure-based Pythagorean fuzzy additive ratio assessment approach and its application to multi-criteria sustainable biomass crop selection. Appl. Soft Comput. 125, 18 (2022)

    Article  MATH  Google Scholar 

  15. Giri, B.C., Molla, M.U., Biswas, P.: Pythagorean fuzzy DEMATEL method for supplier selection in sustainable supply chain management. Expert Syst. Appl. 193, 10 (2022)

    Article  MATH  Google Scholar 

  16. Nan, T.B., Zhang, H., He, Y.: Pythagorean fuzzy full implication Triple I method and its application in medical diagnosis. Int. J. Fuzzy Syst. 24, 2250–2263 (2022)

    Article  MATH  Google Scholar 

  17. Demir, E., Ak, M.F., Sari, K.: Pythagorean fuzzy based AHP-VIKOR integration to assess rail transportation systems in Turkey. Int. J. Fuzzy Syst. 25, 13 (2022)

    MATH  Google Scholar 

  18. Senapati, T., Yager, R.R.: Fermatean fuzzy sets. J. Ambient. Intell. Humaniz. Comput. 11(2), 663–674 (2020)

    Article  MATH  Google Scholar 

  19. Jeevaraj, S.: Ordering of interval-valued Fermatean fuzzy sets and its applications. Expert Syst. Appl. 185, 20 (2021)

    MATH  Google Scholar 

  20. Mishra, A.R., Chen, S.M., Rani, P.: Multiattribute decision making based on Fermatean hesitant fuzzy sets and modified VIKOR method. Inf. Sci. Int. J. 607, 1532–1549 (2022)

    MATH  Google Scholar 

  21. Liu, P.D., Rani, P., Mishra, A.R.: COPRAS method based on interval-valued hesitant Fermatean fuzzy sets and its application in selecting desalination technology. Appl. Soft Comput. 119, 17 (2022)

    MATH  Google Scholar 

  22. Yager, R.R.: Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 25(5), 1 (2016)

    MathSciNet  MATH  Google Scholar 

  23. Peide, L., Shyi-Ming, C., Peng, W.: Multiple-attribute group decision-making based on q-rung orthopair fuzzy power MacLaurin symmetric mean operators. IEEE Trans. Syst. Man Cybern. Syst. 50(10), 1–16 (2018)

    MATH  Google Scholar 

  24. Kumar, K., Chen, S.M.: Group decision making based on q-rung orthopair fuzzy weighted averaging aggregation operator of q-rung orthopair fuzzy numbers. Inf. Sci. 598, 1–18 (2022)

    Article  MATH  Google Scholar 

  25. Farid, H.M.A., Riaz, M.: q-Rung orthopair fuzzy Aczel-Alsina aggregation operators with multi-criteria decision. Eng. Appl. Artif. Intell. 122, 21 (2023)

    Article  MATH  Google Scholar 

  26. Xiao, L.M., et al.: A q-rung orthopair fuzzy decision-making model with new score function and best–worst method for manufacturer selection. Inf. Sci. 608, 153–177 (2022)

    Article  MATH  Google Scholar 

  27. Tang, G.L., et al.: A new integrated multi-attribute decision-making approach for mobile medical app evaluation under q-rung orthopair fuzzy environment. Expert Syst. Appl. 200, 26 (2022)

    Article  MATH  Google Scholar 

  28. Qiyas, M., et al.: Case study for hospital-based Post-Acute Care-Cerebrovascular Disease using Sine Hyperbolic q-rung orthopair fuzzy Dombi aggregation operators. Expert Syst. Appl. 215, 13 (2023)

    Article  MATH  Google Scholar 

  29. Al-Shami, T.M.: (2, 1)-Fuzzy sets: properties, weighted aggregated operators and their applications to multi-criteria decision-making methods. Complex Intell. Syst. 9(2), 1687–1705 (2023)

    Article  MATH  Google Scholar 

  30. Ibrahim, H.Z., Al-Shami, T.M., Elbarbary, O.G.: (3, 2)-Fuzzy Sets and Their Applications to Topology and Optimal Choices. Hindawi Limited, London (2021)

    Book  MATH  Google Scholar 

  31. Al-shami, T.M., et al.: SR-fuzzy sets and their weighted aggregated operators in application to decision-making. J. Funct. Spaces 2022, 14 (2022)

    MathSciNet  MATH  Google Scholar 

  32. Salih, Y.A., Ibrahim, H.Z.: CR-fuzzy sets and their applications. J. Math. Comput. Sci. 28(2), 171–181 (2023)

    Article  MATH  Google Scholar 

  33. Sarkar, B., Chakraborty, D., Biswas, A.: Development of type-2 Pythagorean fuzzy set with its application to sustainable transport system selection. Appl. Soft Comput. 142, 23 (2023)

    Article  MATH  Google Scholar 

  34. Zeng, S.Z., et al.: Social network multiple-criteria decision-making approach for evaluating unmanned ground delivery vehicles under the Pythagorean fuzzy environment. Technol. Forecast. Soc. Change 175, 19 (2022)

    Article  MATH  Google Scholar 

  35. Zulqarnain, R.M., et al.: Einstein ordered weighted aggregation operators for Pythagorean fuzzy hypersoft set with its application to solve MCDM problem. IEEE Access 10, 95294–95320 (2022)

    Article  MATH  Google Scholar 

  36. Farid, H.M.A., Riaz, M.: Pythagorean fuzzy prioritized aggregation operators with priority degrees for multi-criteria decision-making. Int. J. Intell. Comput. Cybern. 15(4), 510–539 (2022)

    Article  MATH  Google Scholar 

  37. Chakraborty, S., Saha, A.K.: Novel Fermatean Fuzzy Bonferroni Mean aggregation operators for selecting optimal health care waste treatment technology. Eng. Appl. Artif. Intell. 119, 16 (2023)

    Article  MATH  Google Scholar 

  38. Mishra, A.R., et al.: Fermatean fuzzy copula aggregation operators and similarity measures-based complex proportional assessment approach for renewable energy source selection. Complex Intell. Syst. 8(6), 5223–5248 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  39. Senapati, T., Yager, R.R.: Fermatean fuzzy weighted averaging/geometric operators and its application in multi-criteria decision-making methods. Eng. Appl. Artif. Intell. 85, 112–121 (2019)

    Article  MATH  Google Scholar 

  40. Jia, Q.L., Herrera-Viedma, E.: Pythagorean fuzzy sets to solve Z-numbers in decision-making model. IEEE Trans. Fuzzy Syst. 31(3), 890–904 (2023)

    Article  MATH  Google Scholar 

  41. Yang, J.X., et al.: MAGDM in hesitant interval-valued Pythagorean linguistic Z-number based on combined score function and entropy. Int. J. Mach. Learn. Cybern. 13(10), 3173–3198 (2022)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by Jilin Science and Technology Development Program Project-Key R&D Program (Grant No. 20210201055GX).

Author information

Authors and Affiliations

  1. Key Laboratory of CNC Equipment Reliability, Ministry of Education, Changchun, 130022, Jilin, China

    Yan Liu, Zhaojun Yang, Jialong He, Guofa Li & Ruiliang Zhang

  2. School of Mechanical and Aerospace Engineering, Jilin University, Changchun, 130022, Jilin, China

    Yan Liu, Zhaojun Yang, Jialong He, Guofa Li & Ruiliang Zhang

Authors
  1. Yan Liu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Zhaojun Yang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Jialong He
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Guofa Li
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Ruiliang Zhang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Jialong He.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Y., Yang, Z., He, J. et al. Some Operators Based on qth Rung Root Orthopair Fuzzy Sets and Their Application in Multi-criteria Decision Making. Int. J. Fuzzy Syst. 26, 1749–1767 (2024). https://doi.org/10.1007/s40815-024-01695-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-024-01695-2

Keywords