Abstract
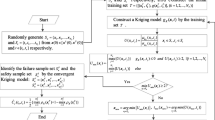
To improve the efficiency of the double-loop fuzzy simulation (DLFS) for estimating the time-dependent failure possibility (TDFP), a single-loop fuzzy simulation (SLFS) is proposed in this paper. In the SLFS, an equivalent transformation formula of TDFP is put forward for the first time, then the estimation of TDFP is transformed into a single-loop fuzzy simulation procedure where the fuzzy inputs and time parameter are sampled in the same level. As only single-loop sampling is needed in the SLFS, the computational complexity and cost of the proposed method are both reduced compared to the DLFS. Subsequently, a single-loop Kriging model based SLFS (ASLK-SLFS) is developed to enhance the performance of the SLFS. Based on the candidate sampling pool of SLFS to sample the fuzzy inputs and the time parameter in the same level, a single Kriging can be more efficiently constructed and updated. To further improve the efficiency of ASLK-SLFS, an improved version is then developed by using a candidate sampling pool reduction strategy. Finally, three examples are employed to illustrate the advantages of the proposed methods. Through the proposed ASLK-SLFS, the safety degree of the time-dependent structure with fuzzy uncertainty can be efficiently evaluated.









Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Data Availability
Not applicable.
Code Availability
Not applicable.
References
Wu, L., Wu, L., Shi, J., Chou, Y.: Project portfolio selection considering uncertainty: stochastic dominance-based fuzzy ranking. Int. J. Fuzzy Syst. (2021). https://doi.org/10.1007/s40815-021-01069-y
Feng, K., Lu, Z., Yun, W.: Aircraft icing severity analysis considering three uncertainty types. AIAA J. 57(4), 1514–1522 (2019). https://doi.org/10.2514/1.j057529
Jin, T., Ding, H., Li, B., Xia, H., Xue, C.: Valuation of interest rate ceiling and floor based on the uncertain fractional differential equation in caputo sense. J Intell. Fuzzy Syst. 1–2, 1–10 (2020). https://doi.org/10.3233/JIFS-201930
Wang, L., Lu, Z., Jia, B.: A decoupled method for credibility-based design optimization with fuzzy variables. Int. J. Fuzzy Syst. 22(3), 844–858 (2020). https://doi.org/10.1007/s40815-020-00813-0
Zhang, H., Ji, Y., Yu, R., Qu, S., Dai, Z.: The robust cost consensus model with interval-valued opinion and uncertain cost in group decision-making. Int. J. Fuzzy Syst. (2021). https://doi.org/10.1007/s40815-021-01168-w
Yousefi, A., Pishvaee, M.S.: A fuzzy optimization approach to integration of physical and financial flows in a global supply chain under exchange rate uncertainty. Int. J. Fuzzy Syst. 20(8), 2415–2439 (2018). https://doi.org/10.1007/s40815-018-0511-6
Guo, S., Zhang, X., Du, Y., Zheng, Y., Cao, Z.: Path planning of coastal ships based on optimized DQN reward function. J. Mar. Sci. Eng. 9, 210 (2021). https://doi.org/10.3390/jmse9020210
Kiureghian, A.D., Ditlevsen, O.: Aleatory or epistemic? Does it matter? Struct. Saf. 31(2), 105–112 (2009). https://doi.org/10.1016/j.strusafe.2008.06.020
Qiu, Z., Wang, J.: The interval estimation of reliability for probabilistic and non-probabilistic hybrid structural system. Eng. Fail. Anal. 17(5), 1142–1154 (2010). https://doi.org/10.1016/j.engfailanal.2010.01.010
Jin, T., Xia, H., Chen, H.: Optimal control problem of the uncertain second-order circuit based on first hitting criteria. Math. Method. Appl. Sci. 44, 882–900 (2021). https://doi.org/10.1002/mma.6796
Park, N.W.: Application of Dempster–Shafer theory of evidence to GIS-based landslide susceptibility analysis. Environ. Earth Sci. 62(2), 367–376 (2011). https://doi.org/10.1007/s12665-010-0531-5
Feng, K., Lu, Z., Yun, W., He, L.: Bi-objective adaptive kriging for reliability analysis with random and evidence variables. AIAA J. 1, 1–15 (2019). https://doi.org/10.2514/1.J058582
Zadeh, L.A.: Fuzzy sets as a basis for a theory of possibility. Fuzzy Set. Syst. 1(1), 3–28 (1978). https://doi.org/10.1016/0165-0114(78)90029-5
Meng, Z., Pang, Y., Pu, Y., Wang, X.: New hybrid reliability-based topology optimization method combining fuzzy and probabilistic models for handling epistemic and aleatory uncertainties. Comput. Method. M. 363, 112886 (2020). https://doi.org/10.1016/j.cma.2020.112886
Cremona, C., Gao, Y.: The possibilistic reliability theory: theoretical aspects and applications. Struct. Saf. 19(2), 173–201 (1997). https://doi.org/10.1016/S0167-4730(97)00093-3
Li, G., Lu, Z., Xu, J.: A fuzzy reliability approach for structures based on the probability perspective. Struct. Saf. 54, 10–18 (2015). https://doi.org/10.1016/j.strusafe.2014.09.008
Wang, C., Qiu, Z., Xu, M., Qiu, H.: Novel fuzzy reliability analysis for heat transfer system based on interval ranking method. Int. J. Therm. Sci. 116, 234–241 (2017). https://doi.org/10.1016/j.ijthermalsci.2017.02.016
Liu, B.: Uncertainty Theory, 2nd edn. Springer, New York (2002)
Jin, T., Ding, H., Xia, H., Bao, J.: Reliability index and asian barrier option pricing formulas of the uncertain fractional first-hitting time model with caputo type. Chaos Soliton. Fract. 142(2), 110409 (2020). https://doi.org/10.1016/j.chaos.2020.110409
Jin, T., Yang, X., Xia, H., Ding, H.: Reliability index and option pricing formulas of the first hitting time model based on the uncertain fractional-order differential equation with caputo type. Fractals 29(1), 2150012 (2020). https://doi.org/10.1142/S0218348X21500122
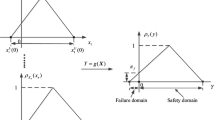
Fan, C., Lu, Z., Shi, Y.: Time-dependent failure possibility analysis under consideration of fuzzy uncertainty. Fuzzy Set. Syst. 367, 19–35 (2019). https://doi.org/10.1016/j.fss.2018.06.016
Feng, K., Lu, Z., Pang, C., Yun, W.: Time-dependent failure credibility analysis and its optimization based computational methods. Eng. Struct. 181, 605–616 (2019). https://doi.org/10.1016/j.engstruct.2018.12.039
Jiang, X., Lu, Z.: An efficient algorithm for time-dependent failure credibility by combining adaptive single-loop kriging model with fuzzy simulation. Struct. Multidisc. Optim. 62(2), 1025–1039 (2020). https://doi.org/10.1007/s00158-020-02609-0
Hu, Z., Mahadevan, S.: A single-Loop Kriging surrogate modeling for time-dependent reliability analysis. J. Mech. Des. 138, 061406 (2016). https://doi.org/10.1115/1.4033428
Lophaven, S. N., Nielsen H. B., Sondergaard J.: DACE, a matlab Kriging toolbox, version 2.0. Technical Report IMM-TR-2002–12; Technical University of Denmark, 2002
Wang, W., Gao, H., Zhou, C., Zhang, Z.: Reliability analysis of motion mechanism under three types of hybrid uncertainties. Mechan. Mach. Theory 121, 769–784 (2018). https://doi.org/10.1016/j.mechmachtheory.2017.12.010
Feng, K., Lu, Z., Wei, N., Li, G.: Adaptive kriging model for fuzzy safety degree analysis to time-dependent structure. AIAA J. 59(9), 1–11 (2020). https://doi.org/10.2514/1.J059834
Funding
This work was supported by the National Natural Science Foundation of China (Grant No. NSFC 12302154, 12272300), and the China Postdoctoral Science Foundation (Grant No. 2023T160488).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.
Appendix: Brief Introduction of Kriging and U-Learning Function
Appendix: Brief Introduction of Kriging and U-Learning Function
In Kriging theory, the actual performance function \(g({\varvec{X}})\) is considered as a realization of the stochastic field \(g_{K} ({\varvec{X}})\) which is written as,
in which \({\varvec{f}}({\varvec{X}}) = [f_{1} ({\varvec{X}}),f_{2} ({\varvec{X}}), \cdots ,f_{{N_{f} }} ({\varvec{X}})]\) represents the \(N_{f}\)-dimensional basis function vector of \({\varvec{X}}\), \({\varvec{\xi}} = \left[ {\xi_{1} ,\xi_{2} , \cdots ,\xi_{{N_{f} }} } \right]^{T}\) expresses the \(N_{f}\)-dimensional regression coefficient vector, and \({\varvec{Z}}\left( {\varvec{X}} \right)\) denotes a stationary Gaussian process with the following statistic characteristics,
in which \({\varvec{x}}_{{j_{1} }}\) and \({\varvec{x}}_{{j_{2} }}\) are the \(j_{1}\) th and \(j_{2}\) th elements among the training sample set, and \(R_{Z}\) is the kernel function that determines the smoothness of the Kriging model. In this paper, the commonly used Gaussian kernel function is used in the Kriging model. The detailed process for constructing the Kriging model can refer to Ref. [25].
For any untrained sample x, the Kriging prediction can be expressed as,
in which N (·) stands for the normal distribution, \(\mu_{{g_{K} }} \left( {\varvec{x}} \right)\) represents the mean of the prediction, and \(\sigma_{{g_{K} }} \left( {\varvec{x}} \right)\) denotes its standard deviation.
Based on the prediction characteristics of the Kriging model \(g_{K} ({\varvec{X}})\), the probability of misidentifying the sign of \(g({\varvec{x}})\) by using \(g_{K} ({\varvec{x}})\) can be expressed as,
in which \(U({\varvec{x}})\) is known as the U learning function, which is defined as,
Eqs. (25) and (26) indicate that the smaller the value of \(U({\varvec{x}})\) is, the higher the probability of misidentifying the sign of \(g({\varvec{x}})\). Generally, the sign of the performance function with respect to the sample with U learning function value not less than 2 can be considered to be accurately predicted, since the state of this samples can be correctly identified by the Kriging model with \(1 - \Phi ( - 2) = 97.7\%\) probability at least.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Feng, K., Lu, Z., Lu, Y. et al. A Single-Loop Fuzzy Simulation-Based Adaptive Kriging Method for Estimating Time-Dependent Failure Possibility. Int. J. Fuzzy Syst. 26, 2553–2566 (2024). https://doi.org/10.1007/s40815-024-01745-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40815-024-01745-9