Skip to main content

Advertisement

Springer Nature Link
Log in

Dissipative Constraint-Based Saturation Control for Fuzzy Markov Jump Systems Within a Finite-Time Interval

  • Published:
International Journal of Fuzzy Systems Aims and scope Submit manuscript

Abstract

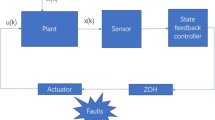
This paper deals with the problems of finite-time boundedness and dissipative analysis for a class of discrete-time nonlinear Markov jump systems (MJSs) with disturbances. In particular, the Takagi-Sugeno fuzzy model is applied to the nonlinear plant, and the impact of time-varying actuator saturation is considered in the controller design. The main purpose of this paper is to develop a mode-dependent fuzzy saturation control for fuzzy MJSs over a finite-time interval. With the help of the Lyapunov stability theory and Abel lemma-based finite-sum inequality, it is established that convergence of all states are confirmed through the addressed control design. Correspondingly, the resulting closed-loop system is stochastically finite-time bounded and \(({\mathcal {Q}},{\mathcal {S}},{\mathcal {R}})\)-\(\gamma\)-dissipative under linear matrix inequality (LMI) framework. At last, two numerical examples are given to demonstrate the effectiveness and usefulness of the obtained LMI conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles, news and stories from top researchers in related subjects.

Data Availability

The authors confirm that the data supporting the findings of this study are available within the article and/or its supplementary materials.

References

  1. Takagi, T., Sugeno, M.: Fuzzy identification of systems and its applications to modeling and control. IEEE Transactions on Systems Man and Cybernetics: Systems. 15, 116–132 (1985)

    Article  MATH  Google Scholar 

  2. Wang, W., Huang, C., Lam, H.K., Wang, L.: Formation control of T-S fuzzy systems with event-triggered sampling scheme via membership function dependent approach. Information Sciences. 622, 842–858 (2023)

    Article  MATH  Google Scholar 

  3. Kwon, O.M., Park, M.J., Park, J.H., Lee, S.M.: Improvement on the feasible region of H∞ performance and stability for systems with interval time-varying delays via augmented Lyapunov-Krasivskii functional. Journal of the Franklin Institute. 353, 4979–5000 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  4. Lian, Z., Shi, P., Lim, C.C., Yuan, X.: Fuzzy-model-based lateral control for networked autonomous vehicle systems under hybrid cyber-attacks. IEEE Transactions on Cybernetics. 53(4), 2600–2609 (2023)

    Article  MATH  Google Scholar 

  5. Park, M.J., Kwon, O.M.: Stability and stabilization of discrete-time T-S fuzzy systems with time-varying delay via Cauchy-Schwartz-based summation inequality. IEEE Transactions on Fuzzy Systems. 25(1), 128–140 (2017)

    Article  MATH  Google Scholar 

  6. Shen, H., Su, L., Park, J.H.: Extended passive filtering for discrete-time singular Markov jump systems with time-varying delays. Signal Processing. 128, 68–77 (2016)

    Article  MATH  Google Scholar 

  7. Tang, F., Wang, H., Chang, X.H., Zhang, L., Alharbi, K.H.: Dynamic event-triggered control for discrete-time nonlinear Markov jump systems using policy iteration-based adaptive dynamic programming. Nonlinear Analysis: Hybrid Systems. 49, 101338 (2023)

    MathSciNet  MATH  Google Scholar 

  8. Li, F., Shen, H.: Asynchronous control of 2-D Markov jump systems subject to general probabilities information. Nonlinear Analysis: Hybrid Systems. 49, 101357 (2023)

    MathSciNet  MATH  Google Scholar 

  9. Wang, G., Shan, H., Li, F., Wang, J.: H∞filtering for discrete-time hidden singular Markov jump systems subject to partially known probability information under DoS attacks. International Journal of Robust and Nonlinear Control. 33(5), 3210–3226 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  10. Kavikumar, R., Sakthivel, R., Kwon, O.M., Kaviarasan, B.: Reliable non-fragile memory state feedback controller design for fuzzy Markov jump systems. Nonlinear Analysis: Hybrid Systems. 35, 100828 (2020)

    MathSciNet  MATH  Google Scholar 

  11. Kong, L., Luo, M., Cheng, J., Wang, X., Shi, K.: Interval type-2 fuzzy dissipative control for multiagent systems with Markovian switching parameters via dynamic event-triggered and double-quantized schemes. International Journal of Fuzzy Systems. 25, 2020–2035 (2023)

    Article  MATH  Google Scholar 

  12. Shen, H., Wu, J., Li, F., Chen, X., Wang, J.: Fuzzy multi-objective fault-tolerant control for nonlinear Markov jump singularly perturbed systems with persistent dwell-time switched transition probabilities. Fuzzy Sets and Systems. 452, 131–148 (2023)

    Article  MathSciNet  MATH  Google Scholar 

  13. Sun, Q., Ran, J., Fu, J.: Robust preview control of uncertain discrete-time T-S fuzzy Markovian jump systems subject to time-varying delays via sliding mode approach. Information Sciences. 639, 118980 (2023)

    Article  MATH  Google Scholar 

  14. Wu, T., Xiong, L., Cao, J., Park, J.H.: Hidden Markov model-based asynchronous quantized sampled-data control for fuzzy nonlinear Markov jump systems. Fuzzy Sets and Systems. 432, 89–110 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  15. Amato, F., Ariola, M., Dorato, P.: Finite-time control of linear systems subject to parametric uncertainties and disturbances. Automatica. 37(9), 1459–1463 (2001)

    Article  MATH  Google Scholar 

  16. He, X., Li, X., Song, S.: Finite-time input-to-state stability of nonlinear impulsive systems. Automatica. 135, 109994 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  17. Liu, X., Wei, X., Li, Y.: Observer-based finite-time fuzzy H∞ control for Markovian jump systems with time-delay and multiplicative noises. International Journal of Fuzzy Systems. 25, 1643–1655 (2023)

    Article  MATH  Google Scholar 

  18. Qi, W., Zhang, C., Zong, G., Su, S.F., Chadli, M.: Finite-time event-triggered stabilization for discrete-time fuzzy Markov jump singularly perturbed systems. IEEE Transactions on Cybernetics. 53(7), 4511–4520 (2023)

    Article  MATH  Google Scholar 

  19. Li, X., Yang, X., Song, S.: Lyapunov conditions for finite-time stability of time-varying time-delay systems. Automatica. 103, 135–140 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  20. Li, X., Song, W., Li, Y., Tong, S.: Finite-time dynamic event-triggered fuzzy output fault-tolerant control for interval type-2 fuzzy systems. IEEE Transactions on Fuzzy Systems. 30(11), 4926–4938 (2022)

    Article  MATH  Google Scholar 

  21. Wang, Y., Xu, S., Ahn, C.K.: Finite-time composite antidisturbance control for T-S fuzzy nonhomogeneous Markovian jump systems via asynchronous disturbance observer. IEEE Transactions on Fuzzy Systems. 30(11), 5051–5057 (2022)

    Article  MATH  Google Scholar 

  22. Li, H., Wang, J., Shi, P.: Output-feedback based sliding mode control for fuzzy systems with actuator saturation. IEEE Transactions on Fuzzy Systems. 24(6), 1282–1293 (2016)

    Article  MATH  Google Scholar 

  23. Ge, C., Zhang, Z., Wang, L., Liu, Y.: Novel stability criteria for sampled-data T-S fuzzy systems with actuator failure. International Journal of Fuzzy Systems. 25, 940–949 (2023)

    Article  MATH  Google Scholar 

  24. Xie, Z., Wang, D., Wong, P.K., Li, W.: Dynamic-output-feedback based interval type-2 fuzzy control for nonlinear active suspension systems with actuator saturation and delay. Information Sciences. 607, 1174–1194 (2022)

    Article  MATH  Google Scholar 

  25. Yan, S., Gu, Z., Park, J.H., Xie, X.: Distributed-delay-dependent stabilization for networked interval type-2 fuzzy systems with stochastic delay and actuator saturation. IEEE Transactions on Systems Man and Cybernetics: Systems. 53(5), 3165–3175 (2023)

    Article  MATH  Google Scholar 

  26. Zhu, H., Li, X., Song, S.: Input-to-state stability of nonlinear impulsive systems subjects to actuator saturation and external disturbance. IEEE Transactions on Cybernetics. 53(1), 173–183 (2023)

    Article  MATH  Google Scholar 

  27. Willems, J.C.: Dissipative dynamical systems part I: General theory. Archive for Rational Mechanics and Analysis. 45(5), 321–351 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  28. Xie, S., Xie, L., Souza, C.E.D.: Robust dissipative control for linear systems with dissipative uncertainty. International Journal of Control. 70(2), 169–191 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  29. Ma, Y., Jia, X., Liu, D.: Finite-time dissipative control for singular discrete-time Markovian jump systems with actuator saturation and partly unknown transition rates. Applied Mathematical Modelling. 53, 49–70 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  30. Chen, G., Yang, J., Zhou, X.: Finite-time dissipative control for discrete-time stochastic delayed systems with Markovian switching and interval parameters. Communications in Nonlinear Science and Numerical Simulation. 110, 106352 (2022)

    Article  MathSciNet  MATH  Google Scholar 

  31. Ran, G., Shu, Z., Lam, H.K., Liu, J., Li, C.: Dissipative tracking control of nonlinear Markov jump systems with incomplete transition probabilities: A multiple-event-triggered approach. IEEE Transactions on Fuzzy Systems. 31(7), 2389–2400 (2023)

    Article  MATH  Google Scholar 

  32. Tao, J., Lu, R., Shi, P., Su, H., Wu, Z.G.: Dissipativity-based reliable control for fuzzy Markov jump systems with actuator faults. IEEE Transactions on Cybernetics. 49, 2377–2388 (2017)

    Article  MATH  Google Scholar 

  33. Zhang, X.M., Han, Q.L.: Abel lemma-based finite-sum inequality and its application to stability analysis for linear discrete time-delay systems. Automatica. 57, 199–202 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported in part by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education under Grant NRF-2020R1A6A1A12047945.

Author information

Authors and Affiliations

  1. School of Electrical Engineering, Chungbuk National University, Cheongju, 28644, South Korea

    Ramasamy Kavikumar, Boomipalagan Kaviarasan & Oh-Min Kwon

  2. Department of Applied Mathematics, Bharathiar University, Coimbatore, 641046, India

    Rathinasamy Sakthivel

  3. Department of Mathematics, Sungkyunkwan University, Suwon, 440746, South Korea

    Rathinasamy Sakthivel

Authors
  1. Ramasamy Kavikumar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Boomipalagan Kaviarasan
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Oh-Min Kwon
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Rathinasamy Sakthivel
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding authors

Correspondence to Oh-Min Kwon or Rathinasamy Sakthivel.

Ethics declarations

Conflict of interest

No potential conflict of interest was reported by the authors.

Ethical Approval

This article does not contain any studies with human participants or animals performed by any authors.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kavikumar, R., Kaviarasan, B., Kwon, OM. et al. Dissipative Constraint-Based Saturation Control for Fuzzy Markov Jump Systems Within a Finite-Time Interval. Int. J. Fuzzy Syst. 27, 77–92 (2025). https://doi.org/10.1007/s40815-024-01761-9

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40815-024-01761-9

Keywords