Abstract
Causal relationships differ from statistical relationships, and distinguishing cause from effect is a fundamental scientific problem that has attracted the interest of many researchers. Among causal discovery problems, discovering bivariate causal relationships is a special case. Causal relationships between two variables (“X causes Y” or “Y causes X”) belong to the same Markov equivalence class, and the well-known independence tests and conditional independence tests cannot distinguish directed acyclic graphs in the same Markov equivalence class. We empirically evaluated the performance of three state-of-the-art models for causal discovery in the bivariate case using both simulation and real-world data: the additive-noise model (ANM), the post-nonlinear (PNL) model, and the information geometric causal inference (IGCI) model. The performance metrics were accuracy, area under the ROC curve, and time to make a decision. The IGCI model was the fastest in terms of algorithm efficiency even when the dataset was large, while the PNL model took the most time to make a decision. In terms of decision accuracy, the IGCI model was susceptible to noise and thus performed well only under low-noise conditions. The PNL model was the most robust to noise. Simulation experiments showed that the IGCI model was the most susceptible to “confounding,” while the ANM and PNL models were able to avoid the effects of confounding to some degree.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
People are generally more concerned with causal relationships between variables than with statistical relationships between variables, and the concept of causality has been widely discussed [9, 12]. The best way to demonstrate a causal relationship between variables is to conduct a controlled randomized experiment. However, real-world experiments are often expensive, unethical, or even impossible. Many researchers working in various fields (economics, sociology, machine learning, etc.) are thus using statistical methods to analyze causal relationships between variables [2, 3, 16, 19, 21, 25, 31, 37, 48, 55].
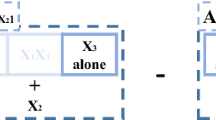
Directed acyclic graphs (DAGs) have been used to formalize the concept of causality [29]. Although a conditional independence test cannot tell the full story of a causal relationship, it can be used to exclude irrelevant relationships between variables [29, 44]. However, a conditional independence test is impossible when there are only two variables. Several models have been proposed to solve this problem [20, 38, 46, 47, 49]. For two variables X and Y, there are at least six possible relationships between them (Fig. 1). The top two diagrams show the independent case and the feedback case, respectively. The middle two show the two possible causal relationships between X and Y: “X causes Y” and “Y causes X.” The bottom two show the “common cause” case and the “selection bias” case. Unobserved variables Z are “confounders”Footnote 1 for causal discovery between X and Y. The existence of “confounders”Footnote 2 creates a spurious correlation between X and Y. Distinguishing spurious correlation due to unobserved confounders from actual causality remains a challenging task in the field of causal discovery. Many models are based on the assumption that no unobserved confounders exist.Footnote 3
In the work reported here, we experimentally compared the performance of three state-of-the-art causal discovery model, the additive-noise model (ANM) [15], the post-nonlinear (PNL) model [54], and the information geometric causal inference (IGCI) model [22]. We used three metrics: accuracy, area under the ROC curve (AUC), and time to make a decision. This paper is an extended and revised version of our conference paper [23]. It includes new AUC results and the updated time to make a decision for the PNL model. It also describes typical examples of model failure and discusses the reasons for failure. Finally, it describes new experiments on the responses of the models to spurious correlation caused by confounders using simulation and real-world data.
In Sect. 2, we discuss related work in the field of causal discovery. In Sect. 3, we briefly describe the three models. In Sect. 4, we describe the dataset we used and the implementations of the three models. In Sect. 5, we present the results and give a detailed analysis of the performances of the three models. We conclude in Sect. 6 by summarizing the strengths and weaknesses of the three models and mentioning future tasks.
2 Related work
Temporal information is useful for causal discovery modeling [30, 32]. Granger [7] proposed detecting the causal direction of time series data on the basis of the temporal ordering of the variables and used linear systems to make it more operational. He formulated the definition of causality in terms of conditional independence relations [8]. Chen et al. extended the linear stochastic systems he proposed [7] to work on nonlinear systems [1]. Shajarisales et al. [39] proposed using the spectral independence criterion (SIC) for causal inference from time series data and a mechanism different from that used in Granger causality and compared the two methods. For Granger causality [7] and extended Granger causality [1], temporal information is needed. When discovering causal relationship from time series data, the data resolution might be different from the true causal frequency. Gong et al. [6] discussed this issue and showed that using non-Gaussian of data can help identify the underlying model under some conditions.
Shimizu et al. [41] proposed using a linear non-Gaussian acyclic model (LiNGAM for short) to detect the causal direction of variables without the need for temporal information. LiNGAM works when the causal relationship between variables is linear, the distributions of disturbance variables are non-Gaussian, and the network structure can be expressed using a DAG. Several extensions of LiNGAM have been proposed [14, 18, 40, 42].
LiNGAM is based on the assumption of linear relationships between variables. Hoyer et al. [15] proposed using an additive- noise model (ANM) to deal with nonlinear relationships. If the regression function is linear, ANM works in the same way as LiNGAM. Zhang et al. [52,53,54, 56] proposed using a PNL model that takes into account the nonlinear effect of causes, inner additive noise, and external sensor distortion. The ANM and PNL model are briefly introduced in the following section.
While the above models are based on structural equation modeling (SEM), which requires structural constraints on the data generating process, another research direction is based on the assumption that independent mechanisms in nature generate causes and effects. The idea is that the shortest description of joint distribution \(p(\mathrm {cause, effect})\) can be expressed by \(p(\mathrm {cause})p(\mathrm {effect|cause})\). Compared with factorization into p(cause)p(effect|cause), p(effect)p(cause|effect) has lower total complexity. Although comparing total complexity is an intuitive idea, Kolmogorov complexity and algorithmic information could be used to measure it [19].
Janzing et al. [4, 22] proposed IGCI to infer asymmetry between cause and effect through the complexity loss of distributions. The IGCI model is briefly introduced in the following section. Zhang et al. [57] proposed using a bootstrap-based approach to detect causal direction. It is based on the assumption that the parameters of the causes involved in the causality data generation process are exogenous to those of the cause to the effect. Stegle et al. [45] proposed using a probabilistic latent variable model (GPI) to distinguish between cause and effect using standard Bayesian model selection.
In addition to the above studies on the causal relationship between two variables, there have been several reviews. Spirtes et al. discussed the main concepts of causal discovery and introduced several models based on SEM [43]. Eberhardt [5] discussed the fundamental assumptions of causal discovery and gave an overview of related causal discovery methods. Several methods have been proposed for deciding the causal direction between two variables, and specific methods have been compared. However, as far as we know, there has been little discussion of how to fairly compare methods based on different assumptions. In the work described above, accuracy was usually used as the evaluation metric. Another commonly used metric for a binary classifier is the AUC. Compared with accuracy, the ROC curve can show the trade-off between the true-positive rate (TPR) and the false-positive rate (FPR) of a binary classifier. In our framework for causal discovery models, we use AUC as an evaluation metric. We have used it to obtain several new insights. We also used the time to make a decision as an evaluation metric since it may become a performance bottleneck when dealing with big data.
3 Models
We used the ANM, the PNL model, and the IGCI model in the comparison experiments. The ANM and PNL model define how causality data are generated in nature through SEM. The assumption of additive noise is enlightening. The IGCI model finds the asymmetry between cause and effect through the complexity loss of distributions. The assumption of IGCI is intuitive and how well it works needs to be further researched.
3.1 ANM
The additive-noise model of Hoyer et al. [15] is based on two assumptions: (1) the observed effects (Y) can be expressed using functional models of the cause (X) and additive noise (N) (Eq. 1); (2) the cause and additive noise are independent. If f() is a linear function and the noise has a non-Gaussian distribution, the ANM works in the same way as LiNGAM [41]. The model is learned by performing regression in both directions and testing the independence between the assumed cause and noise (residuals) for each direction. The decision rule is to choose the direction with the less dependence as the true causal direction. The ANM cannot handle the linear Gaussian case since the data can fit the model in both directions, so the asymmetry between cause and effect disappears. Gretton et al. improved the algorithm and extended the ANM to work even in the linear Gaussian case [50]. The improved model also works more efficiently in the multivariate case.
3.2 PNL model
In the post-nonlinear model of Zhang et al. [53, 54], effects are nonlinear transformations of causes with some inner additive noise, followed by external nonlinear distortion (Eq. 2). From Eq. 2, we obtain \(N={f}^{-1}(Y)-g(X)\), where X and Y are the two observed variables representing cause and effect, respectively. To identify the cause and effect, a particular type of constrained nonlinear ICA [17, 53] is performed to extract two components that are as independent as possible. The two extracted components are the assumed cause and corresponding additive noise, respectively. The identification method of the model is described elsewhere ([53], Section 4). The identifiability of the causal direction inferred by the PNL model has been proven [54]. The PNL model can identify the causal direction of data generated in accordance with the model except for the five situations described in Table 1 in [54].
3.3 IGCI
The IGCI model [4, 22] is based on the hypothesis that if “X causes Y,” the marginal distribution p(x) and the conditional distribution p(y|x) are independent in a particular way. The IGCI model gives an information-theoretic view of additive noise and defines independence by using orthogonality. With ANM [15], if there is no additive noise, inference is impossible, while it is possible with the IGCI model.
The IGCI model determines the causal direction on the basis of complexity loss. According to IGCI, the choice of p(x) is independent of the choice of f for the relationship \(y=f(x)+n\). Let \(\nu _{x}\) and \(\nu _{y}\) be the reference distributionsFootnote 4 for X and Y.
is the KL-distance between \(P _{x}\) and \(\nu _{x}\). \(D(P_{x} \left| \right| \nu _{x})\) works as a feature of the complexity of the distribution. The complexity loss from X to Y is given by
The decision rule of the IGCI model is that if \(V_{X\rightarrow Y} < 0\), infer “X causes Y,” and if \(V_{X\rightarrow Y} > 0\), infer “Y causes X.” This rule is rather theoretical. An applicable and explicit form for the reference measure is entropy-based IGCI or slope-based IGCI.
-
1.
Entropy-based IGCI:
$$\begin{aligned} \hat{S}(P_{X}) := \psi (m)-\psi (1)+\frac{1}{m-1}\sum _{i=1}^{m-1}\log |x_{i+1}-x_{i}|\nonumber \\ \end{aligned}$$(3)where \(\psi ()\) is the digamma functionFootnote 5 and m is the number of data points.
$$\begin{aligned} \hat{V}_{X\rightarrow Y} := \hat{S}(P_{Y})-\hat{S}(P_{X})=-\hat{V}_{Y\rightarrow X} \end{aligned}$$(4) -
2.
Slope-based IGCI:
$$\begin{aligned} \hat{V}_{X\rightarrow Y} := \frac{1}{m-1}\sum _{i=1}^{m-1}\log \left| \frac{y_{i+1}-y_{i}}{x_{i+1}-x_{i}} \right| \end{aligned}$$(5)
These explicit forms are simpler, and we can see that the two calculation methods coincide. The calculation does not take much time even when dealing with a large amount of data. However, the IGCI model assumes that the causal process is noiseless and may perform poorly under high-noise conditions. We discuss the performance of the three models in Sect. 5.
4 Experiments
Here we describe the dataset used in our experiments and the implementation of each model.
4.1 Dataset
We used the cause effect pairs (CEP) [27] dataset, which contains 97 pairs of real-world causal variables with the cause and effect labeled for each pair. The dataset is publicly available online [27]. Some of the data were collected from the UCI machine learning repository [24]. The data come from various fields, including geography, biology, physics, and economics. The dataset also contains time series data. Most of the data are noisy. An appendix in [28] contains a detailed description of each pair of variables.
We used 91 of the pairs in our experiments since some of the data (e.g., pair0052) contain multi-dimensional variables.Footnote 6 The 91 pairs are listed in Table 4 in “Appendix.” Some contain the same variables collected in different countries or at different times.Footnote 7 The variables range in size from 126 to 16,382.Footnote 8 The variety of data types in the CEP dataset makes causal analysis using real-world data challenging.
4.2 Implementation
We implemented the three models following the original work [15, 22, 53]. A brief introduction is given blow.
ANM Using the reported experimental settings [15], we performed Gaussian processes for machine learning regression [33,34,35]. We then used the Hilbert–Schmidt Independence Criterion (HSIC) [10] to test the independence between the assumed cause and residuals. The dataset used had been labeled with the true causal direction for each pair with no cases of independence or feedback. Using the decision rule of ANM, we determined that the direction with the greater independence was the true causal direction.
PNL Model We used a particular type of constrained nonlinear ICA to extract the two components that would be the cause and noise if the model had been learned in the correct direction. The nonlinearities of g() and \(f^{-1}()\) in Eq. 2 were modeled using multilayer perceptrons. By minimizing the mutual information between the two output components, we made the output as independent as possible. After extracting two independent components, we tested their independence by using the HSIC [10, 11]. Finally, in the same way as for the ANM, we determined that the direction with the greater independence was the correct one.
IGCI \(\mathrm {(entropy, uniform)}\) Compared with the first two models, the implementation of the IGCI (entropy, uniform) model was simpler. We used reported equations (3, 4) to calculate \(\hat{V}_{X\rightarrow Y}\) and \(\hat{V}_{Y\rightarrow X}\) and determined that the direction in which entropy decreased was the correct direction. If \(\hat{V}_{X\rightarrow Y}<0\), the inferred causal direction was “X causes Y”; otherwise, it was “Y causes X.” For the IGCI model, the data should be normalized before calculating \(\hat{V}_{X\rightarrow Y}\) and \(\hat{V}_{Y\rightarrow X}\). In accordance with the reported experimental results, we used the uniform distribution as the reference distribution because of its good performance. For the repetitive data in the dataset, we set \(\log 0=0\).
IGCI \(\mathrm {(slope, uniform)}\) The implementation of the IGCI (slope, uniform) model was similar to that of the IGCI (entropy, uniform) one. We used Eq. 5 to calculate \(\hat{V}_{X\rightarrow Y}\) and \(\hat{V}_{Y\rightarrow X}\) and determined that the direction with a negative value was the correct one. For the same reason as above, we normalized the data to [0,1] before calculating \(\hat{V}_{X\rightarrow Y}\) and \(\hat{V}_{Y\rightarrow X}\). To make Eq. 5 meaningful, we filtered out the repetitive data.
5 Results
Here, we first compare model accuracy for different decision rates.Footnote 9 We changed the threshold and calculated the corresponding decision rate and accuracy for each model. The accuracy of the models for different decision rates has been compared in the original study [4]. Compared with [4], we used more real-world data in our experiments. Besides, how accuracy changed under different decision rates was showed. Our results are consistent with those shown of Mooij et al. [26]. The performance of the models for different decision rates is discussed in Sect. 5.1.
Since causal discovery models in the bivariate case make a decision between two choices, we can regard these models as binary classifiers and evaluate them using AUC. We previously divided the data into two groups (inferred as “X causes Y” and inferred as “Y causes X”) and evaluated the performance of each model for each group [23]. Here we give the results for the entire (undivided) dataset.
Finally, we compare model efficiency by using the average time needed to make a decision. This is described in Sect. 5.3.
5.1 Accuracy for different decision rates
We calculated the accuracy of each model for different decision rates using Eqs. 6 and 7. The results are plotted in (Fig. 2). The decision rate changed when the threshold was changed. The larger the threshold, the more stringent the decision rule. In an ideal situation, accuracy decreases as the decision rate increases, with the starting point at 1.0. However, the results with real-world data were not perfect because the data were noisy.
As shown in Fig. 2, the accuracy started from 1.0 for the ANM and IGCI and from 0.0 for the PNL model. This means that the PNL model made an incorrect decision when it had the highest confidence. Although the accuracies of the IGCI models started from 1.0, they dropped sharply when the decision rate was between 0 and 0.2. The reasons for this are discussed in detail in Sect. 5.4. After reaching a minimum, the accuracies increased almost continuously and stabilized. The accuracy of the ANM was more stable than those of the other models. When all decisions had been made, the model accuracies were ranked IGCI > ANM > PNL.
5.2 Area under ROC curve (AUC)
Besides calculating the accuracy of the three models for different decision rates, we used the AUC to evaluate their performance. Some of the experimental results were presented in our conference paper [23], for which the dataset was divided into two groups: inferred as “X causes Y” and inferred as “Y causes X.” Here we present updated experimental results for the entire dataset.
The following steps were taken to get the experimental results:
-
1.
Set X as the cause and Y as the effect in the input data.
-
2.
Set \({V}_{X \rightarrow Y}\) and \({V}_{Y \rightarrow X}\) to be the outputs.
-
3.
Calculate the absolute value of the difference between \({V}_{X \rightarrow Y}\) and \({V}_{Y \rightarrow X}\) (Eq. 8) and map \(V_{\mathrm {diff}}\) to [0,1].
-
4.
Assign a positive label to the pairs inferred as “X causes Y” and a negative one to the pairs inferred as “Y causes X.”
-
5.
Use \(V_{\mathrm {diff}}\) and the labels assigned in step 4 to calculate the true-positive rate (TPR) and false-positive rate (FPR) for different thresholds.
-
6.
Plot the ROC curve and calculate the corresponding AUC value.
In step (1), instead of dividing the data into two groups as done previously [23], we set the input matrix so that the first column was the cause and the second column was the effect. Then, if the inferred causal direction for a pair was “X causes Y,” a positive label was assigned to that pair; otherwise, a negative label was assigned.
In step (3), we used the absolute value of the difference between \({V}_{X \rightarrow Y}\) and \({V}_{Y \rightarrow X}\) as the “confidence” of the model when making a decision. The larger the \(V_{\mathrm {diff}}\), the greater the confidence. We did not use division because, if one of \({V}_{X \rightarrow Y}\) and \({V}_{Y \rightarrow X}\) was very small, the division result would be very large. We mapped \(V_{\mathrm {diff}}\) to [0,1] to make the calculation more convenient. In this way, \(V_{\mathrm {diff}}\) could be used in the same way as the output of a binary classifier. For causal discovery, the larger the \(V_{\mathrm {diff}}\), the greater the confidence in the decision. At the same time, more punishment should be given when the decision is incorrect.
In step (4), we labeled the data in accordance with the inferred causal direction. Since the correct label for all the pairs was “X causes Y,” if the inferred result for a pair was “Y causes X,” it was assigned a negative label.
In step (5), we used the normalized \(V_{\mathrm {diff}}\) and the label assigned in step (4) to calculate TPR and FPR for different thresholds. We plotted TPR and FPR to get the ROC curve and calculated the corresponding AUC value.
The ROC results are plotted in Fig. 3. The corresponding AUC values are shown in Table 1. Different from the results shown in Fig. 2, both IGCI models performed poorly in terms of AUC. The AUC values for IGCI were smaller than 0.5, which means their performances were even worse than that of a random classifier. However, as described in Sect. 5.1, when we used different decision rates, the IGCI models had better performance.
We checked the decisions made by the IGCI models and found that they made several incorrect decisions when the threshold was large. Such decisions with a large threshold are punished severely when using the AUC metric. As shown in Fig. 2, although the accuracies of the IGCI models started from 1.0, they dropped sharply when the decision rate was between 0 and 0.2. An incorrect decision with a low decision rate was not punished much when evaluating accuracy for different decision rates. However, for the AUC, an incorrect decision when the threshold was large was punished more than when the threshold was small. For these reasons, the starting point of the ROC curve for the IGCI models in Fig. 3 was shifted to the right, making the AUC less than 0.5. In Sect. 5.4, we will discuss why the IGCI models failed.
5.3 Algorithm efficiency
Besides comparing the accuracy and ROC of the three models, we also compared the average time for the algorithm to make a decision.Footnote 10 We performed the experiment on the MATLAB platform with an Intel Core i7-4770 3.40 GHz CPU and 8 GB memory. From Table 2, we can see that the IGCI models were the most efficient one, while the PNL model was the least efficient. The ANM was in the middle. The longer time to make a decision for the PNL model was due to the estimation procedure of \({f}^{-1}\) and g in Eq. 2.
5.4 Typical examples of model failure
5.4.1 Discretization
In Sect. 5.1, we explained that the PNL model gives an incorrect decision when the threshold is set the highest, i.e., the accuracy for different decision rates starts from 0.0. We investigated the reason for the PNL model making an incorrect decision when the threshold was the highest. We found that it happens due to the discretization of data. A scatter plot for a pair of variables (pair0070) is shown in Fig. 4. The data have two variables. Variable \({x}_{1}\) is a value between 0 and 14 reflecting the features of an artificial face. It is used to decide whether the face is that of a man or a woman. A value of 0 means very female, and a value of 14 means very male. Variable \({x}_{2}\) is a value of 0 (female) or 1 (male) reflecting the gender decision. Since variable \({x}_{2}\) has only two values, no matter what nonlinear transformation is made to \({x}_{2}\), the transformation result is two discretized values. According to the mechanism of the PNL model, \(x_{2}\) with two discretized values is inferred to be the cause since the independency is larger if \({x}_{2}\) is the cause. In fact, for this pair of variables, all three models made incorrect decisions in our experiments. For the ANM, the discretization of data makes regression analysis difficult. And the poor regression results negatively affect testing of the independence between the assumed cause and residuals using HSIC. For IGCI, to make Eqs. 3 and 5 meaningful, the repetitive data have to be filtered out. This means that only a few data points are actually used in the final IGCI calculation.
5.4.2 Noisiness
In Sect. 5.1, we showed that IGCI had good performance in general. However, its accuracy dropped sharply when the decision rate was between 0 and 0.2. The reason for this is that it made incorrect decisions with high confidence when dealing with pair0056-pair00 63. These eight pairs contain much noise, which degraded model performance. Moreover, there were outliers for the eight pairs, which greatly affected the decision result. A scatter plot for one example pair is shown in Fig. 5 (pair0056). It shows that the two variables have relatively small correlation and that there are outliers in the data. The calculation method used in IGCI is such that these kinds of outliers affect the inference result more than the other data points. The incorrect decisions that IGCI made about pair0056-pair0063 account for the small AUC value for the IGCI models given in Sect. 5.2. The ANM also made an incorrect inference about these pairs. This is because noise and outliers make overfitting more likely to occur for these variables. For these noisy pairs, the PNL model had the best performance.
5.5 Response to spurious correlation caused by “confounding”
A causal relationship differs from a statistical one, and a statistical relationship is usually not enough to explain a causal one. Even if we observe that two variables are highly correlated, we cannot say that they have a causal relationship. As shown in Table 4 in “Appendix,” the causal direction of the variables in CEP is obvious by common sense. The dataset has been collected for evaluating causal discovery models, and the causal direction of most pairs is obvious from knowledge. However, the relationships of variables that are of general interest in the real world are usually more controversial, e.g., smoking and lung cancer, for which the existence of confounding is usually a bone of contention. A good causal discovery model for two variables should have the ability to avoid the effect of “confounding” to some degree. To test how the ANM, the PNL model, and IGCI perform when dealing with spurious correlation caused by confounding, we first simulated the “common cause” case shown in Fig. 1. We controlled the data generating process to simulate different degrees of confounding. In addition to simulation, we used real-world data from the CEP to evaluate model performance when dealing with real-world data.
5.5.1 Simulation
We conducted simulation experiments of the “common cause” confounding case shown in Fig. 1. We generated data using two equations: \(x=a \times z^{3}+b \times n_{1}\) and \(y=a \times z+b \times n_{2}\), where \(z,n_{1},n_{2} \in U(0,1)\). We used the quotient a / b to control the degree of confounding. There was no direct causal relationship between variables x and y except for the various degrees of confounding. Scatter plots of the data generated using five different quotients are shown in Fig. 6.
We used the generated data to test the performance of the three models. We performed ten random experiments for each quotient and calculated the average of the inferred results. The experimental results are shown in Figs. 7, 8, and Table 3. For IGCI, when the degree of confounding was low, the mean of the estimated resultsFootnote 11 was almost zero. Each estimated result got a positive or negative value randomly. As the degree of confounding increased, the estimated results tended to approve “Y causes X.” For the PNL model, the independence assumptions for both directions were accepted when \(a/b=0.1, 1, 10\) (\(\alpha =0.01\)) and the means of the test statistics (Equation 4 in [11]) were almost equal. When \(a/b=100\), the PNL model rejected the independence assumption for direction “X causes Y” and accepted that “Y causes X.” When a/b was even larger, the independence assumptions were rejected for both directions, especially that of “X causes Y.” For the ANM, when the degree of confounding was low, the independence assumptions were accepted for both directions. When the degree was high, the independence assumptions were rejected for both directions, especially “X causes Y.” From these results, we can see that the IGCI is the most susceptible of the three models tested to confounding, while the PNL model and the ANM can avoid the effect of confounding to a certain extent.
5.5.2 Real-world data
In addition to the simulation experiments described above, we conducted experiments using real-world data. The generation of real- world data can be very complex, which increases the difficulty of the causal discovery task. Here we describe the “common cause” and “selection bias” cases (Fig. 1).
Common cause case Although data for “common cause” are not included in the CEP dataset, some CEP pairs contain the same cause, as shown in “Appendix.” We combined data containing the same cause to obtain pairs of variables, such as “length and diameter.”Footnote 12 A scatter plot of the results is shown in Fig. 9 for the pair “length, diameter.” For the ANM, the p value for the forward direction, “length causes diameter,” was \(8.28 \times 10^{-5}\) while that for the backward direction was \(1.05 \times 10^{-3}\). For the PNL model, the independence test statistic was \(1.11 \times 10^{-3}\) for the forward direction and \(9.50 \times 10^{-4}\) for the backward direction. For IGCI, the result estimated by calculating the entropy was 0.2197, while the other was 0.056. For this pair, although the tendency was not strong, the three models tended to approve “diameter is the cause of length.”
Selection bias case Although there is no causal relationship between X and Y in the selection bias case, independence does not hold between X and Y when conditioned on variable Z. This is the well-known Berkson paradox.Footnote 13 We used the variables “altitude and longitude” (Fig. 10) contained in CEP to test how the three models perform when dealing with the “selection bias” case. The variables were obtained by combining “cause: altitude, effect: temperature” and “cause: longitude, effect: temperature.” The data came from 349 weather stations in Germany [27]. A scatter plot of the results is shown in Fig. 10. For the ANM, the p value for the forward direction, “altitude causes longitude,” was \(4.21 \times 10^{-2}\) while that for the backward direction was \(8.73 \times 10^{-2}\). The independence assumptions were accepted for both directions although “longitude causes altitude” was favored. For the PNL model, the test statistic was \(2.46 \times 10^{-3}\) for the forward direction and \(3.30 \times 10^{-3}\) for the backward direction. The independence assumptions were accepted for both directions, and the independence test results were similar. For IGCI, the result estimated by calculating the entropy was 1.2742 and that estimated by calculating the slope was 1.9032. Both results were positive, and the estimated causal direction was “longitude causes altitude.” Although there should be no causal relationship between “altitude” and “longitude,” it was hard for the three models to determine that from the limited amount of observational data available.
For most cases of causal discovery in the real world, only limited observational data can be obtained, and in some cases the data are incomplete. Moreover, for the case of two variables, the causal sufficiency assumption [36] is easily violated if there is an unobserved common cause. The limited amount of data and unobserved confounders make causal discovery in the bivariate case challenging.
6 Conclusion
We compared three state-of-the-art models (ANM, PNL model, IGCI) for causal discovery in the binary case using simulation and real-world data. Testing using different decision rates showed that the three models had similar accuracies when all the decisions were made. To check whether the decisions made were reasonable, we used a binary classifier metric: the area under the ROC curve (AUC). The IGCI model had a small AUC value because it made several incorrect decisions when the threshold was high. Compared with those of the other models, the accuracy of the ANM was relatively stable. A comparison of the time to make a decision showed that IGCI was the fastest even when the dataset was large. The PNL model took the most time to make a decision.
Of the three models, the IGCI one had the best performance when there was little noise and the data were not discretized much. Improving the performance of the IGCI model when there is much noise and how to deal with discretized data are future tasks. Although the performance of the ANM was relatively stable, overfitting should be avoided for ANM because it will negatively affect the subsequent independence test. Of the three models, the PNL model is the most generalized one as it takes into account the nonlinear effect of causes, inner additive noise, and external sensor distortion. However, estimation procedure of g() and \({f}^{-1}()\) is a lengthy procedure. Finally, testing the responses of the models to “confounding” showed that the ANM and the PNL model can avoid the effect of “confounding” to some degree, while IGCI is the most susceptible to confounding.
Notes
The number of “confounders” is not limited to one.
Reference distributions are used to measure the complexity of \(P_{x}\) and \(P_{y}\). In [22], non-informative distributions like uniform and Gaussian ones are recommended.
The three models we evaluated cannot deal with multi-dimensional data.
Country and time information is not included in the table.
To avoid overfitting, we limited the size to 500 or less.
Since all three models have two outputs, e.g., \(\hat{V}_{X\rightarrow Y}\), \(\hat{V}_{Y\rightarrow X}\) corresponding to the two possible causal directions, we set thresholds based on the absolute difference between them \(|\hat{V}_{X \rightarrow Y}-\hat{V}_{Y \rightarrow X}|\) for use in deciding each decision rate and model accuracy.
Compared to our previous report [23], we reduced the program output so that the PNL model works faster. We have updated the results for time to make a decision for the PNL model accordingly.
We used the difference between \(\hat{V}_{X\rightarrow Y}\) and \(\hat{V}_{Y\rightarrow X}\) (Eqs. 4, 5) as the estimated result. For IGCI, \(\hat{V}_{X\rightarrow Y}\) is the opposite of \(\hat{V}_{Y\rightarrow X}\) if there is no repetitive data. Thus, we can infer that the correct causal direction is \(X\rightarrow Y\) if the estimated result is negative and that \(Y\rightarrow X\) is correct if the estimated result is positive.
The pair “length, diameter” was created from “cause: rings (abalone), effect: length” and “cause: rings (abalone), effect: diameter” using data for abalone [24].
References
Chen, Y., Rangarajan, G., Feng, J., Ding, M.: Analyzing multiple nonlinear time series with extended granger causality. Phys. Lett. A 324(1), 26–35 (2004)
Chen, Z., Zhang, K., Chan, L.: Causal discovery with scale-mixture model for spatiotemporal variance dependencies. In: Advances in Neural Information Processing Systems, pp. 1727–1735 (2012)
Chen, Z., Zhang, K., Chan, L., Schölkopf, B.: Causal discovery via reproducing kernel hilbert space embeddings. Neural Comput. 26(7), 1484–1517 (2014)
Daniusis, P., Janzing, D., Mooij, J., Zscheischler, J., Steudel, B., Zhang, K., Schölkopf, B.: Inferring deterministic causal relations. arXiv preprint arXiv:1203.3475 (2012)
Eberhardt, F.: Introduction to the foundations of causal discovery. Int. J. Data Sci. Anal., 1–11 (2017)
Gong, M., Zhang, K., Schoelkopf, B., Tao, D., Geiger, P.: Discovering temporal causal relations from subsampled data. In: Proceedings of 32th International Conference on Machine Learning (ICML 2015) (2015)
Granger, C.W.: Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 37, 424–438 (1969)
Granger, C.W.: Testing for causality: a personal viewpoint. J. Econ. Dyn. Control 2, 329–352 (1980)
Granger, C.W.: Some recent development in a concept of causality. J. Econom. 39(1), 199–211 (1988)
Gretton, A., Herbrich, R., Smola, A., Bousquet, O., Schölkopf, B.: Kernel methods for measuring independence. J. Mach. Learn. Res. 6(Dec), 2075–2129 (2005)
Gretton, A., Fukumizu, K., Teo, C.H., Song, L., Schölkopf, B., Smola, A.J., et al.: A kernel statistical test of independence. NIPS 20, 585–592 (2008)
Halpern, J.Y.: A modification of the halpern-pearl definition of causality. arXiv preprint arXiv:1505.00162 (2015)
Howards, P.P., Schisterman, E.F., Poole, C., Kaufman, J.S., Weinberg, C.R.: “Toward a clearer definition of confounding” revisited with directed acyclic graphs. Am. J. Epidemiol. 176(6), 506–511 (2012)
Hoyer, P.O., Shimizu, S., Kerminen, A.J., Palviainen, M.: Estimation of causal effects using linear non-gaussian causal models with hidden variables. Int. J. Approx. Reason. 49(2), 362–378 (2008)
Hoyer, P.O., Janzing, D., Mooij, J.M., Peters, J., Schölkopf, B.: Nonlinear causal discovery with additive noise models. In: Advances in neural information processing systems, pp. 689–696 (2009)
Huang, B., Zhang, K., Schölkopf, B.: Identification of time-dependent causal model: A gaussian process treatment. In: The 24th International Joint Conference on Artificial Intelligence, Machine Learning Track, pp. 3561–3568. Buenos, Argentina (2015)
Hyvärinen, A., Oja, E.: Independent component analysis: algorithms and applications. Neural Netw. 13(4), 411–430 (2000)
Hyvärinen, A., Zhang, K., Shimizu, S., Hoyer, P.O.: Estimation of a structural vector autoregression model using non-gaussianity. J. Mach. Learn. Res. 11(May), 1709–1731 (2010)
Janzing, D., Scholkopf, B.: Causal inference using the algorithmic markov condition. IEEE Trans. Inf. Theory 56(10), 5168–5194 (2010)
Janzing, D., Hoyer, P.O., Schölkopf, B.: Telling cause from effect based on high-dimensional observations. arXiv preprint arXiv:0909.4386 (2009)
Janzing, D., MPG, T., Schölkopf, B.: Causality: Objectives and assessment (2010)
Janzing, D., Mooij, J., Zhang, K., Lemeire, J., Zscheischler, J., Daniušis, P., Steudel, B., Schölkopf, B.: Information-geometric approach to inferring causal directions. Artif. Intell. 182, 1–31 (2012)
Jing, S., Satoshi, O., Haruhiko, S., Masahito, K.: Evaluation of causal discovery models in bivariate case using real world data. In: Proceedings of the International MultiConference of Engineers and Computer Scientists 2016, pp. 291–296 (2016)
Lichman, M.: UCI machine learning repository. http://archive.ics.uci.edu/ml (2013)
Lopez-Paz, D., Muandet, K., Schölkopf, B., Tolstikhin, I.: Towards a learning theory of cause-effect inference. In: Proceedings of the 32nd International Conference on Machine Learning. JMLR: W&CP, Lille, France (2015)
Mooij, J.M., Janzing, D., Schölkopf, B.: Distinguishing between cause and effect. In: NIPS Causality: Objectives and Assessment, pp. 147–156 (2010)
Mooij J.M., Janzing, D., Zscheischler, J., Schölkopf, B.: Cause effect pairs repository. https://webdav.tuebingen.mpg.de/cause-effect/ (2014a)
Mooij, J.M., Peters, J., Janzing, D., Zscheischler, J., Schölkopf, B.: Distinguishing cause from effect using observational data: methods and benchmarks. arXiv preprint arXiv:1412.3773 (2014b)
Pearl, J., et al.: Models, reasoning and inference (2000)
Peters, J., Janzing, D., Gretton, A., Schölkopf, B.: Detecting the direction of causal time series. In: Proceedings of the 26th Annual International Conference on Machine Learning, pp. 801–808. ACM, New York (2009)
Peters, J., Mooij, J., Janzing, D., Schölkopf, B.: Identifiability of causal graphs using functional models. arXiv preprint arXiv:1202.3757 (2012)
Peters, J., Janzing, D., Schölkopf, B.: Causal inference on time series using restricted structural equation models. In: Advances in Neural Information Processing Systems, pp. 154–162 (2013)
Rasmussen, C.E.: Gaussian Processes for Machine Learning. MIT press, Cambridge (2006)
Rasmussen, C.E., Nickisch, H.: Gaussian processes for machine learning (gpml) toolbox. J. Mach. Learn. Res. 11(Nov), 3011–3015 (2010a)
Rasmussen, C.E., Nickisch, H.: GPML code. http://www.gaussianprocess.org/gpml/code/matlab/doc/ (2010b)
Scheines, R.: An introduction to causal inference (1997)
Schölkopf, B., Janzing, D., Peters, J., Sgouritsa, E., Zhang, K., Mooij, J.: On causal and anticausal learning. arXiv preprint arXiv:1206.6471 (2012)
Sgouritsa, E., Janzing, D., Hennig, P., Schölkopf, B.: Inference of cause and effect with unsupervised inverse regression. In: AISTATS (2015)
Shajarisales, N., Janzing, D., Schoelkopf, B., Besserve, M.: Telling cause from effect in deterministic linear dynamical systems. arXiv preprint arXiv:1503.01299 (2015)
Shimizu, S., Bollen, K.: Bayesian estimation of causal direction in acyclic structural equation models with individual-specific confounder variables and non-gaussian distributions. J. Mach. Learn. Res. 15(1), 2629–2652 (2014)
Shimizu, S., Hoyer, P.O., Hyvärinen, A., Kerminen, A.: A linear non-gaussian acyclic model for causal discovery. J. Mach. Learn. Res. 7(Oct), 2003–2030 (2006)
Shimizu, S., Inazumi, T., Sogawa, Y., Hyvärinen, A., Kawahara, Y., Washio, T., Hoyer, P.O., Bollen, K.: Directlingam: a direct method for learning a linear non-gaussian structural equation model. J. Mach. Learn. Res. 12(Apr), 1225–1248 (2011)
Spirtes, P., Zhang, K.: Causal discovery and inference: concepts and recent methodological advances. Appl. Inform. 3, 3 (2016)
Spirtes, P., Glymour, C.N., Scheines, R.: Causation, Prediction, and Search. MIT press, Cambridge (2000)
Stegle, O., Janzing, D., Zhang, K., Mooij, J.M., Schölkopf, B.: Probabilistic latent variable models for distinguishing between cause and effect. In: Advances in Neural Information Processing Systems, pp. 1687–1695 (2010)
Sun, X., Janzing, D., Schölkopf, B.: Causal inference by choosing graphs with most plausible markov kernels. In: ISAIM (2006)
Sun, X., Janzing, D., Schölkopf, B.: Distinguishing between cause and effect via kernel-based complexity measures for conditional distributions. In: ESANN, pp. 441–446 (2007a)
Sun, X., Janzing, D., Schölkopf, B., Fukumizu, K.: A kernel-based causal learning algorithm. In: Proceedings of the 24th international conference on Machine learning, pp. 855–862. ACM, New York (2007b)
Sun, X., Janzing, D., Schölkopf, B.: Causal reasoning by evaluating the complexity of conditional densities with kernel methods. Neurocomputing 71(7), 1248–1256 (2008)
Tillman, R.E., Gretton, A., Spirtes, P.: Nonlinear directed acyclic structure learning with weakly additive noise models. In: Advances in Neural Information Processing Systems, pp. 1847–1855 (2009)
Weinberg, C.R.: Toward a clearer definition of confounding. Am. J. Epidemiol. 137(1), 1–8 (1993)
Zhang, K., Chan, L.W.: Extensions of ICA for causality discovery in the Hong Kong stock market. In: International Conference on Neural Information Processing, pp. 400–409. Springer, Berlin (2006)
Zhang, K., Hyvärinen, A.: Distinguishing causes from effects using nonlinear acyclic causal models. In: Journal of Machine Learning Research, Workshop and Conference Proceedings (NIPS 2008 Causality Workshop), vol. 6, pp. 157–164 (2008)
Zhang, K., Hyvärinen, A.: On the identifiability of the post-nonlinear causal model. In: Proceedings of the Twenty-fifth Conference on Uncertainty in Artificial Intelligence, pp. 647–655. AUAI Press, Corvallis (2009)
Zhang, K., Schölkopf, B., Janzing, D.: Invariant gaussian process latent variable models and application in causal discovery. arXiv preprint arXiv:1203.3534 (2012)
Zhang, K., Wang, Z., Schölkopf, B.: On estimation of functional causal models: post-nonlinear causal model as an example. In: 2013 IEEE 13th International Conference on Data Mining Workshops, pp. 139–146. IEEE (2013)
Zhang, K., Zhang, J., Schölkopf, B.: Distinguishing cause from effect based on exogeneity. arXiv preprint arXiv:1504.05651 (2015)
Acknowledgements
We thank the anonymous reviewers for their helpful comments to improve the paper. The work was supported in part by a Grant-in-Aid for Scientific Research (15K12148) from the Japan Society for the Promotion of Science.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper is an revised and extended version of our conference paper [23].
Appendix: Pairs of variables used in experiment
Appendix: Pairs of variables used in experiment
See Table 4.
Rights and permissions
About this article
Cite this article
Song, J., Oyama, S. & Kurihara, M. Tell cause from effect: models and evaluation. Int J Data Sci Anal 4, 99–112 (2017). https://doi.org/10.1007/s41060-017-0063-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41060-017-0063-0