Skip to main content
SpringerLink
Log in

Recent advance in machine learning for partial differential equation

  • Regular Paper
  • Published:
CCF Transactions on High Performance Computing Aims and scope Submit manuscript

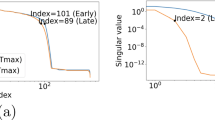
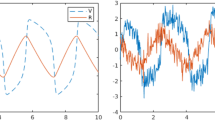
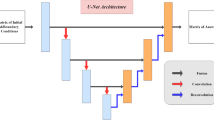
Abstract

Machine learning method has been applied to solve different kind of problems in different areas due to the great success in several tasks such as computer vision, natural language processing and robotic in recent year. In scientific computing community, it is well-known that solving partial differential equations, which are naturally derived from physical rules that describe some of phenomena, is a challenging task in terms of computational efficiency and model accuracy. On the other hand, machine learning models are data-driven that purely reply on learning the pattern of the data distribution. Researcher recently proposed a few new frameworks to solve certain kind of partial differential equations with machine learning technique. In this paper, we discuss two newly developed machine learning based methods for solving partial differential equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Aarts, L.P., Van der Veer, P.: Solving nonlinear differential equations by a neural network method. In: Computational Science—ICCS (2001)

  • Breiman, L.: Random forests. Mach. Learn. (2001)

  • Breiman, L., Friedman, J.H., Olshen, R.A., Stone, C.J.: Classification and regression trees. Wadsworth and Brooks Cole Advanced Books and Software, Monterey (1984)

    MATH  Google Scholar 

  • Bristeau, M.O., Glowinski, R., Periaux, J.: Numerical methods for the Navier-stokes equations. Applications to the simulation of compressible and incompressible viscous flows. Comput. Phys. Rep. 6, 73–187 (1987)

    Article  MathSciNet  Google Scholar 

  • Chang, B. Meng, L. Haber, E., Ruthotto, L., Begert, D., Holtham, E.: Reversible architectures for arbitrarily deep residual neural networks. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence. New Orleans, LA, pp 2811–2818 (2018)

  • Chen, Z., Badrinarayanan, V., Lee, C.-Y., Rabinovich, A.: Gradnorm: gradient normalization for adaptive loss balancing in deep multitask networks. In: International Conference on Machine Learning, pp 794–803. PMLR, (2018a)

  • Chen, T.Q., Rubanova, Y., Bettencourt, J., Duvenaud, D.: Neural ordinary differential equations. In: Advances in Neural Information Processing Systems 31 (NeurIPS 2018), Montreal, Canada (2018b)

  • Cheung, K.C., Ling, L.: A kernel-based embedding method and convergence analysis for surfaces PDEs. SIAM J. Sci. Comput. 40(1), A266–A287 (2018)

    Article  MathSciNet  Google Scholar 

  • Cheung, K.C., Ling, L., Schaback, R.: \(H^2\)-convergence of least-squares kernel collocation methods. SIAM J. Numer. Anal. 56(1), 614–633 (2018)

    Article  MathSciNet  Google Scholar 

  • Cortes, C., Vapnik, V.: Support-vector networks. Mach. Learn. 20, 273–297 (1995)

    MATH  Google Scholar 

  • Elbrächter, D., Grohs, P., Jentzen, A., Schwab, C.: DNN Expression rate analysis of high-dimensional PDEs: application to option pricing. arXiv:1809.07669. (2018)

  • Flamant, C., Protopapas, P., Sondak, D.: Solving differential equations using neural network solution bundles. arXiv:2006.14372 (2020)

  • Forgy, E.W.: Cluster analysis of multivariate data: efficiency versus interpretability of classifications. Biometrics 21, 768–769 (1965)

    Google Scholar 

  • González-García, R., Rico-Martínez, R., Kevrekidis, I.G.: Identification of distributed parameter systems: a neural net based approach. Comp. Chem. Eng. 22, S965–S968 (1998)

    Article  Google Scholar 

  • Guo, P., Huang, K., Xu, Z.: Partial differential equations is all you need for generating neural architectures. arXiv preprint arXiv:2103.08313, (2021)

  • Haber, E., Ruthotto, L.: Stable architectures for deep neural networks. Inverse Prob. 34(1), 1–22 (2017)

    MathSciNet  MATH  Google Scholar 

  • Hasan, A., Pereira, J. M., Ravier, R., Farsiu, S., Tarokh, V.: Learning partial differential equations from data using neural networks. In: ICASSP 2020–2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, pp. 3962–3966 (2020)

  • Hayati, M., Karami, B.: Feedforward neural network for solving partial differential equations. J. Appl. Sci. 7, 2812–2817 (2007)

    Article  Google Scholar 

  • He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, (2016), pp 770-778, https://doi.org/10.1109/CVPR.2016.90

  • Hennigh, O., Narasimhan, S., Nabian, M. A., Subramaniam, A., Tangsali, K., Rietmann, M., Ferrandis, J.A., Byeon, W., Fang, Z., Choudhry, S.: NVIDIA SimNet: an AI-accelerated multi-physics simulation framework. arXiv:2012.07938. (2020)

  • Hermann, J., Schätzle, Z., Noé, F.: Deep-neural-network solution of the electronic Schrödinger equation. Nat. Chem. 12, 891–897 (2020)

    Article  Google Scholar 

  • Hochreiter, S., Schmidhuber, J.: Long short-term memory. Neural Comput. 9, 1735–1780 (1997)

    Article  Google Scholar 

  • Huré, C., Pham, H., Warin, X.: Deep backward schemes for high-dimensional nonlinear PDEs. (2020). ffhal-02005362v2f

  • Jiequn, H., Arnulf, J., Weinan, E.: Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. 115, 8505–8510 (2018)

    Article  MathSciNet  Google Scholar 

  • Jin, X., Cai, S., Li, Hui, K., George E.: Nsfnets (navier-stokes flow nets): physics-informed neural networks for the incompressible Navier-stokes equations. arXiv preprint arXiv:2003.06496, (2020)

  • Karumuri, S., Tripathy, R., Bilionis, I., Panchal, J.: Simulator-free solution of high-dimensional stochastic elliptic partial differential equations using deep neural networks. J. Comput. Phys. 404, 109120 (2020)

    Article  MathSciNet  Google Scholar 

  • Kingma, D. P., Adam, J.B.: A method for stochastic optimization. arXiv:1412.6980, (2014)

  • Kramer, Mark A.: Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 37, 233–243 (1991)

    Article  Google Scholar 

  • Lagaris, I.E., Likas, A., Fotiadis, D.I.: Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 9, 987–1000 (1998)

    Article  Google Scholar 

  • LeCun, Y., Boser, B., Denker, J.S., Henderson, D., Howard, R.E., Hubbard, W., Jackel, L.D.: Backpropagation applied to handwritten zip code recognition. ATT Bell Laboratories, (1989)

    Book  Google Scholar 

  • Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B., Bhattacharya, K., Stuart, A., Anandkumar, A.: Neural operator: graph kernel network for partial differential equations. arXiv preprint arXiv:2003.03485 (2003)

  • Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B., Bhattacharya, K., Stuart, A., Anandkumar, A.: Multipole graph neural operator for parametric partial differential equations. arXiv preprint arXiv:2006.09535 (2006)

  • Li, Z., Kovachki, N., Azizzadenesheli, K., Liu, B., Bhattacharya, K., Stuart, A., Anandkumar, A.: Fourier neural operator for parametric partial differential equations. arXiv preprint arXiv:2010.08895 (2010)

  • Li, X., Wong, T.-K., Leonard, C., Ricky T. Q., Duvenaud, D.: Proceedings of the twenty third international conference on artificial intelligence and statistics, PMLR 108:3870–3882, (2020a)

  • Li, Y., Lu, J., Mao, A.: Variational training of neural network approximations of solution maps for physical models. J. Comput. Phys. 409, 109338 (2020b)

    Article  MathSciNet  Google Scholar 

  • Lloyd, S.P.: Least square quantization in PCM. Bell Telephone Laboratories Paper, (1957)

  • Long, Z., Lu, Y., Ma, X., Dong, B.: PDE-Net: learning PDEs from data. arXiv:1710.09668. (2018)

  • Long, Z., Lu, Y., Dong, B.: PDE-Net 2.0: learning PDEs from data with a numeric-symbolic hybrid deep network. arXiv:1812.04426, (2019)

  • Lu, Y., Zhong, A., Li, Q., Dong, B.: Beyond finite layer neural networks: Bridging deep architectures and numerical differential equations. arXiv preprint arXiv:1710.10121, (2017)

  • Lu, L., Meng, X., Mao, Z., Karniadakis, G. E.: DeepXDE: a deep learning library for solving differential equations. arXiv:1907.04502. (2020)

  • MacQueen, J. B.: Some methods for classification and analysis of multivariate observations. In: Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability, (1967)

  • Martin, M., Faisal, Q., Hendrick, de H.: Neural networks trained to solve differential equations learn general representations. Adv. Neural Inform. Process. Syst. (2018)

  • McCulloch, W.S., Pitts, W.: A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5(4), 115–133 (1943)

    Article  MathSciNet  Google Scholar 

  • Meurer, A., Smith, C.P., Paprocki, M., Certík, O., Kirpichev, S.B., Rocklin, M., Kumar, A., Ivanov, S., Moore, J.K., Singh, S., et al.: Sympy: symbolic computing in python. PeerJ Comput. Sci. 3, e103 (2017)

    Article  Google Scholar 

  • Raissi, M.: Deep hidden physics models: deep learning of nonlinear partial differential equations. J. Mach. Learn. Res. 19, 932–955 (2018)

    MathSciNet  MATH  Google Scholar 

  • Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019)

    Article  MathSciNet  Google Scholar 

  • Ruthotto, L., Haber, E.: Deep neural networks motivated by partial differential equations. arXiv preprint arXiv:1804.04272, (2018)

  • She, J.-H., Grecu, D.: Neural network for CVA: learning future values. Papers 1811.08726, arXiv.org(2018) (2018)

  • Sirignano, J., Spiliopoulos, K.: DGM: a deep learning algorithm for solving partial differential equations. J. Comput. Phys. 375, 1339–1364 (2018)

    Article  MathSciNet  Google Scholar 

  • Sitzmann, V., Martel, J.N.P., Bergman, A.W., Lindell, D.B., Wetzstein, G.: Implicit neural representations with periodic activation functions. arXiv preprint arXiv:2006.09661, (2020)

  • Sommerfeld, A.: Partial differential equations in physics. Academic Press, New York (1949)

    MATH  Google Scholar 

  • Stefan, K., Alexander, S., Michaela, S.: A deep neural network algorithm for semilinear elliptic PDEs with applications in insurance mathematics. Risks 8, 136 (2020)

    Article  Google Scholar 

  • Steinhaus, H.: Sur la division des corps matériels en parties Bull. Acad. Polon. Sci. (1957)

  • Tancik, M., Srinivasan, P. P., Mildenhall, B., Fridovich-Keil, S., Raghavan, N., Singhal, U., Ramamoorthi, R., Barron, J.T.: Ren Ng. Fourier features let networks learn high frequency functions in low dimensional domains. arXiv preprint arXiv:2006.10739, (2020)

  • Tang, B., Pan, Z., Yin, K., Khateeb, A.: Recent advances of deep learning in bioinformatics and computational biology. Front. Genet. 10, 214 (2019)

    Article  Google Scholar 

  • Tompson, J., Schlachter, K., Sprechmann, P., Perlin, K.: Accelerating Eulerian Fluid SimulationWith Convolutional Networks. In: Proceedings of the 34th International Conference on Machine Learning, (2017)

  • Wang, S., Teng, Y., Perdikaris, P.: Understanding and mitigating gradient pathologies in physics-informed neural networks. arXiv preprint arXiv:2001.04536, (2020a)

  • Wang, S., Yu, X., Perdikaris, P.: When and why pinns fail to train: a neural tangent kernel perspective. arXiv preprint arXiv:2007.14527, (2020b)

  • Weinan, E., Han, J., Jentzen, A.: Deep learning-based numerical methods for high-dimensional parabolic partial differential equations and backward stochastic differential equations. Commun. Math. Stat. 5, 349–380 (2017)

    Article  MathSciNet  Google Scholar 

  • Yu, Y., Hientzsch, B., Ganesan, N.: Backward deep BSDE methods and applications to nonlinear problems. arXiv:2006.07635. (2020)

  • Zhang, D., Guo, L., Karniadakis, G.E.: Learning in modal space: solving time-dependent stochastic PDEs using physics-informed neural networks. SIAM J. Sci. Comput. 42, A639–A665 (2020)

    Article  MathSciNet  Google Scholar 

  • Zhaoxia, P., Eugenia, K.: Models, numerical methods, and data assimilation, numerical weather prediction basics. Springer, Berlin (2019)

    Google Scholar 

Download references

Acknowledgements

We gratefully thank the Dr. Sanjay Choudhry and Zongyi Li for providing support and comment. We also thank the anonymous reviewer for their useful suggestions.

Author information

Authors and Affiliations

  1. NVIDIA AI Technology Centre, NVIDIA Corp, Shatin N.T., Hong Kong

    Ka Chun Cheung & Simon See

Authors
  1. Ka Chun Cheung
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Simon See
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ka Chun Cheung.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cheung, K.C., See, S. Recent advance in machine learning for partial differential equation. CCF Trans. HPC 3, 298–310 (2021). https://doi.org/10.1007/s42514-021-00076-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42514-021-00076-7

Keywords

Search

Navigation