Skip to main content

Advertisement

Springer Nature Link
Log in

Periodic Analysis of Resistive Random Access Memory (RRAM)-Based Swish Activation Function

  • Original Research
  • Published:
SN Computer Science Aims and scope Submit manuscript

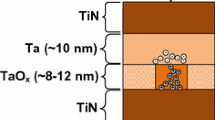
Abstract

Activation functions are one of the key parameters in deep neural networks. They help decide the output and its functionality for a given application. In software, variety of activation functions, such as sigmoid, TanH, ReLU, ELU, GeLU, SELU, SiLU/Swish, etc., have been investigated for machine learning applications, whereas the hardware implementation of the activation functions is sub-ordinate in literature. This paper proposes a novel hardware design of swish (self-gated) activation function for analog applications using Resistive Random Access Memory (RRAM). The approximate analog equivalent model of swish circuit helps capture the incremental changes in the output voltage or current. The periodic analysis of the swish equivalent model has been performed on the parameters, such as power, area and total harmonic distortion, at different temperature ranges. The analog hardware design of the swish circuit has been implemented in UMC 180 nm technology node. The simulation results show low power of 498 μW attained for the swish circuit. The area occupied by the swish circuit is 15.12 μm2.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig.2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Goodfellow I, Bengio Y, Courville A. Deep learning. MIT Press, pp198–201. 2016.

  2. Tabarce S, Tavares V, Oliveira P. Programmable analogue VLSI implementation for asymmetric sigmoid neural activation function and its derivative. Electron Lett. 2005;41:863–4. https://doi.org/10.1049/el:20052024.

    Article  Google Scholar 

  3. Ramachandran P, Zoph B, Le QV. Swish: a self-gated activation function. Google Brain. 2017;1–12

  4. Fatima A, Pethe A. NVM device-based deep inference architecture using self-gated activation functions (Swish). In: Bajpai MK, Kumar Singh K, Giakos G. (eds) Machine vision and augmented intelligence—theory and applications. Lecture notes in electrical engineering. 2021;796. Springer, Singapore. https://doi.org/10.1007/978-981-16-5078-9_4.

  5. Chen PY, Yu S. Compact modeling of RRAM devices and its applications in 1T1R and 1S1R array design. IEEE Trans Electron Devices. 2015;62(12):4022–8.

    Article  MathSciNet  Google Scholar 

  6. International Roadmap for Devices and Systems, “Beyond CMOS”, IEEE, 2020 [Online] Available: https://irds.ieee.org/editions/2020/beyond-cmos

  7. Burr GW, Shelby RM, Sebastian A, Kim S, Kim S, Sidler S, Virwani K, Ishii M, Narayanan P, Fumarola A, Sanches LL, Boybat I, Le Gallo M, Moon K, Woo J, Hwang H, Leblebici Y. Neuromorphic computing using non-volatile memory. Adv Phys X. 2017;2(1):89–124.

    Google Scholar 

  8. Yu S. Neuro-inspired computing with emerging nonvolatile memory. IEEE. 2018;106(2):260–85.

    Article  Google Scholar 

  9. Rajendran B, Alibart F. Neuromorphic computing based on emerging memory technologies. IEEE J Emerg Select Top Circ Syst. 2016;6(2):198–211.

    Article  Google Scholar 

  10. Yu S, Sun X, Peng X, Huang S. Compute-in-memory with emerging non-volatile memories: challenges and prospects. In: IEEE Custom Integrated Circuits Conference (CICC), Boston, MA, USA, pp. 1–4, 23, 2020.

  11. Chou C, et al. An N40 256K×44 embedded RRAM macro with SL-precharge SA and low-voltage current limiter to improve read and write performance. In: IEEE International Solid–State Circuits Conference—(ISSCC), San Francisco, CA, pp. 478–480, 2018.

  12. Hyungjun K, Taesu K, Jinseok K, Jae-Joon K. Deep neural network optimized to resistive memory with nonlinear current–voltage characteristics. J Emerg Technol Comput Syst. 2018. https://doi.org/10.1145/3145478.

    Article  Google Scholar 

  13. Kuzum D, Yu S, Wong H-SP. Synaptic electronics: materials, devices and applications. IOP Sci Nanotechnol. 2013;24(38).

  14. Sepp H, Jurgen S. Long short-term memory. Neural Comput. 1997;9(8):1735–80.

    Article  Google Scholar 

  15. Rupesh KS, Klaus G, Jurgen S. Highway networks. arXiv preprint. https://arxiv.org/abs/1505.00387, 2015.

  16. Xavier G, Antoine B, Yoshua B. Deep sparse rectifier neural networks. In: Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics, pp. 315–323, 2011.

  17. Stephen AB, Markus M. Fast and slow contrast adaptation in retinal circuitry. Neuron. 2002;36(5):909–19.

    Article  Google Scholar 

  18. Real E, Asari H, Gollisch T, Meister M. Neural circuit inference from function to structure. Curr Biol. 2017;27(2):189–98.

    Article  Google Scholar 

  19. Yeo I, Gi S, Lee B, Chu M. Stochastic implementation of the activation function for artificial neural networks. In: 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, pp. 440–443, 2016. https://doi.org/10.1109/BioCAS.2016.7833826.

  20. Ito Y. Approximation of functions on a compact set by finite sums of a sigmoid function without scaling. Neural Netw. 1991;4(6):817–26.

    Article  Google Scholar 

  21. Wang Z. A four-transistor four-quadrant analog multiplier using MOS transistors operating in the saturation region. IEEE Trans Instrum Meas. 1993;42(1):75–7. https://doi.org/10.1109/19.206689.

    Article  Google Scholar 

  22. Analog Devices. Analog Multipliers, Datasheet: MT-079 Tutorial, [Online], Available: https://www.analog.com/media/en/training-seminars/tutorials/MT-079.pdf

  23. Behzad R. Fundamentals of microelectronics. Hoboken: Wiley; 2014.

    Google Scholar 

  24. Liu S, Nagel LW. Small-signal MOSFET models for analog circuit design. IEEE J Sol State Circ. 1982;17(6):983–98. https://doi.org/10.1109/JSSC.1982.1051852.

    Article  Google Scholar 

  25. Al-Ruwaihi KM. CMOS analogue neurone circuit with programmable activation functions utilising MOS transistors with optimised process/device parameters. 1997;144(6): 318–322

  26. Gunhee H, Sanchez-Sinencio E. CMOS transconductance multipliers: a tutorial. In: IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, vol. 45, no. 12, pp. 1550–1563, 1998. https://doi.org/10.1109/82.746667.

  27. Wang S-J, Lee J-Y, Chang C-Y. An efficient and reliable approach for semiconductor device parameter extraction. IEEE Trans Comput Aided Des Integr Circuits Syst. 1986;5(1):170–9. https://doi.org/10.1109/TCAD.1986.1270184.

    Article  Google Scholar 

  28. Binkley DM. Tradeoffs and optimization in analog CMOS design. In: 2007 14th International Conference on Mixed Design of Integrated Circuits and Systems, Ciechocinek, Poland, pp. 47–60, 2007. https://doi.org/10.1109/MIXDES.2007.4286119.

  29. Nicholas gerard timmons, andrew rice, approximating activation functions. http://arxiv.org/abs/2001.06370, 17 Jan 2020.

  30. Roman-Loera A, Veerabathini A, Flores-Oropeza LA, Ramirez-Angulo J. A high-frequency small-signal model for four-port network MOSFETs. In: 2020 IEEE 63rd International Midwest Symposium on Circuits and Systems (MWSCAS), Springfield, MA, USA, pp. 53–56, 2020. https://doi.org/10.1109/MWSCAS48704.2020.9184475.

Download references

Author information

Authors and Affiliations

  1. Electrical and Electronics Engineering Department, Birla Institute of Technology and Science Pilani, K K Birla Goa Campus, 403726, Chicalim, Goa, India

    Afroz Fatima & Abhijit Pethe

Authors
  1. Afroz Fatima
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Abhijit Pethe
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Afroz Fatima.

Ethics declarations

Conflict of Interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This article is part of the topical collection “Advances in Machine Vision and Augmented Intelligence” guest edited by Manish Kumar Bajpai, Ranjeet Kumar, Koushlendra Kumar Singh and George Giakos.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Fatima, A., Pethe, A. Periodic Analysis of Resistive Random Access Memory (RRAM)-Based Swish Activation Function. SN COMPUT. SCI. 3, 202 (2022). https://doi.org/10.1007/s42979-022-01059-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42979-022-01059-3

Keywords