Skip to main content

Advertisement

Springer Nature Link
Log in

Statistical Inference on the Shannon and Rényi Entropy Measures of Generalized Exponential Distribution Under the Progressive Censoring

  • Original Research
  • Published:
SN Computer Science Aims and scope Submit manuscript

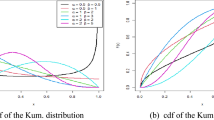
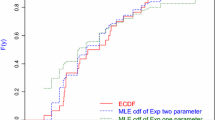
Abstract

The aim of this paper is twofold. First, the estimation of the Shannon and Rényi entropy measures of a generalized exponential distribution is discussed when data are progressively censored. The maximum-likelihood estimates are obtained. The Bayes estimates with respect to three loss functions are proposed. It is assumed that the unknown parameters have independent gamma priors. The closed-form expressions of the Bayes estimates cannot be obtained. Therefore, Lindley’s approximation and importance sampling methods are employed. The asymptotic confidence intervals are computed. The normal approximation of the maximum-likelihood estimate and the log-transformed maximum-likelihood estimate are used. In addition, bootstrap algorithms are used to compute the confidence intervals. Highest posterior density credible intervals of the entropy functions are developed. A detailed numerical study is performed to compare the proposed estimates with respect to their average values and the mean squared errors. The confidence intervals are compared with respect to the average lengths. A real dataset is considered to illustrate the proposed methods. Furthermore, different criteria are proposed for the comparison of various sampling schemes. Then, the optimal sampling scheme for a given criterion is obtained.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

References

  1. Arnold BC, Press SJ. Bayesian inference for Pareto populations. J Economet. 1983;21(3):287–306.

    Article  MathSciNet  Google Scholar 

  2. Balakrishnan N. Progressive censoring methodology: an appraisal. Test. 2007;16(2):211–59.

    Article  MathSciNet  Google Scholar 

  3. Balakrishnan N, Cramer E. The art of progressive censoring: applications to reliability and quality. New York: Birkhauser; 2014.

    Book  Google Scholar 

  4. Balakrishnan N, Sandhu R. A simple simulational algorithm for generating progressive type-II censored samples. Am Stat. 1995;49(2):229–30.

    Google Scholar 

  5. Chen D, Lio Y. Parameter estimations for generalized exponential distribution under progressive type-I interval censoring. Comput Stat Data Anal. 2010;54(6):1581–91.

    Article  MathSciNet  Google Scholar 

  6. Chen M-H, Shao Q-M. Monte carlo estimation of Bayesian credible and HPD intervals. J Comput Graph Stat. 1999;8(1):69–92.

    MathSciNet  Google Scholar 

  7. Cho Y, Sun H, Lee K. An estimation of the entropy for a Rayleigh distribution based on doubly-generalized Type-II hybrid censored samples. Entropy. 2014;16(7):3655–69.

    Article  MathSciNet  Google Scholar 

  8. Cho Y, Sun H, Lee K. Estimating the entropy of a Weibull distribution under generalized progressive hybrid censoring. Entropy. 2015;17(1):102–22.

    Article  Google Scholar 

  9. Efron B, Tibshirani R. Bootstrap methods for standard errors, confidence intervals, and other measures of statistical accuracy. Stat Sci. 1986;1(1):54–75.

    MathSciNet  MATH  Google Scholar 

  10. Eun S-K, Jung N-S, Lee J-J, Bae Y-J. Uncertainty of agricultural product prices by information entropy model using probability distribution for monthly prices. J Korean Soc Agric Eng. 2012;54(2):7–14.

    Google Scholar 

  11. Golan A, Judge GG, Miller D. Maximum entropy econometrics: Robust estimation with limited data. New York: Wiley; 1996.

    MATH  Google Scholar 

  12. Greene WH. Econometric analysis. 4th ed. Pearson Education India; 2003.

  13. Guo L, Gui W. Statistical inference of the reliability for generalized exponential distribution under progressive type-II censoring schemes. IEEE Trans Reliab. 2018;67(2):470–80.

    Article  Google Scholar 

  14. Gupta RD, Kundu D. Theory and methods: generalized exponential distributions. Aust New Zeal J Stat. 1999;41(2):173–88.

    Article  Google Scholar 

  15. Hall P. Theoretical comparison of bootstrap confidence intervals. Ann Stat. 1988;16(3):927–53.

    MathSciNet  MATH  Google Scholar 

  16. Harte D, Vere-Jones D. The entropy score and its uses in earthquake forecasting. Pure Appl Geophys. 2005;162(6–7):1229–53.

    Article  Google Scholar 

  17. Ismail AA. Inference in the generalized exponential distribution under partially accelerated tests with progressive type-II censoring. Theor Appl Fract Mech. 2012;59(1):49–56.

    Article  MathSciNet  Google Scholar 

  18. Kamavaram S, Goseva-Popstojanova K. Entropy as a measure of uncertainty in software reliability, 13th Int’l Symp. Software Reliability Engineering, pp. 209–210. 2002.

  19. Kang S-B, Cho Y-S, Han J-T, Kim J. An estimation of the entropy for a double exponential distribution based on multiply type-II censored samples. Entropy. 2012;14(2):161–73.

    Article  MathSciNet  Google Scholar 

  20. Kayal S, Kumar S, Vellaisamy P. Estimating the Rényi entropy of several exponential populations. Braz J Prob Stat. 2015;29(1):94–111.

    Article  Google Scholar 

  21. Kundu D. Bayesian inference and life testing plan for the Weibull distribution in presence of progressive censoring. Technometrics. 2008;50(2):144–54.

    Article  MathSciNet  Google Scholar 

  22. Kundu D. Bayesian inference and life testing plan for the Weibull distribution in presence of progressive censoring. Qual Control Appl Stat. 2009;54(1):99–100.

    Google Scholar 

  23. Kundu D, Pradhan B. Bayesian inference and life testing plans for generalized exponential distribution. Sci China Ser Math. 2009;52(6):1373–88.

    Article  MathSciNet  Google Scholar 

  24. Kundu D, Pradhan B. Estimating the parameters of the generalized exponential distribution in presence of hybrid censoring. Commun Stat Theory Methods. 2009;38(12):2030–41.

    Article  MathSciNet  Google Scholar 

  25. Lawless JF. Statistical models and methods for lifetime data. Hoboken: Wiley; 2011.

    MATH  Google Scholar 

  26. Lee K, Cho Y. Bayesian and maximum likelihood estimations of the inverted exponentiated half logistic distribution under progressive type-II censoring. J Appl Stat. 2017;44(5):811–32.

    Article  MathSciNet  Google Scholar 

  27. Lindley DV. Approximate Bayesian methods. Trabajos de estadística y de investigación operativa. 1980;31(1):223–45.

    Article  MathSciNet  Google Scholar 

  28. Mahmoudi E. The beta generalized Pareto distribution with application to lifetime data. Math Comput Simul. 2011;81(11):2414–30.

    Article  MathSciNet  Google Scholar 

  29. Maiti K, Kayal S. Estimation for the generalized Fréchet distribution under progressive censoring scheme. Int J Syst Assur Eng Manag. 2019;10(5):1276–301.

    Article  Google Scholar 

  30. Maiti K, Kayal S. Estimation of parameters and reliability characteristics for a generalized Rayleigh distribution under progressive type-II censored sample. Commun Stat Simul Comput. 2021;50(11):3669–98.

    Article  MathSciNet  Google Scholar 

  31. Mohie El-Din M, Amein M, Shafay A, Mohamed S. Estimation of generalized exponential distribution based on an adaptive progressively type-II censored sample. J Stat Comput Simul. 2017;87(7):1292–304.

    Article  MathSciNet  Google Scholar 

  32. Mudholkar GS, Srivastava DK, Kollia GD. A generalization of the Weibull distribution with application to the analysis of survival data. J Am Stat Assoc. 1996;91(436):1575–83.

    Article  MathSciNet  Google Scholar 

  33. Nalewajski RF. Applications of the information theory to problems of molecular electronic structure and chemical reactivity. Int J Mol Sci. 2002;3(4):237–59.

    Article  Google Scholar 

  34. Ng H, Chan PS, Balakrishnan N. Optimal progressive censoring plans for the Weibull distribution. Technometrics. 2004;46(4):470–81.

    Article  MathSciNet  Google Scholar 

  35. Nowak W, Guthke A. Entropy-based experimental design for optimal model discrimination in the geosciences. Entropy. 2016;18(11):409.

    Article  Google Scholar 

  36. Patra LK, Kayal S, Kumar S. Estimating a function of scale parameter of an exponential population with unknown location under general loss function. Stat Pap. 2018;1–17.

  37. Prabakaran S. Application of thermodynamics entropy concept in financial markets. Int Conf Appl Econ. Springer, pp. 13–28. 2017.

  38. Pradhan B, Kundu D. On progressively censored generalized exponential distribution. Test. 2009;18(3):497–515.

    Article  MathSciNet  Google Scholar 

  39. Rass S, König S. Password security as a game of entropies. Entropy. 2018;20(5):312.

    Article  MathSciNet  Google Scholar 

  40. Rényi A. On measures of entropy and information. In: Proceedings of the 4th berkeley symposium on mathematical statistics and probability. 1, 547–561. 1961.

  41. Shannon CE. A mathematical theory of communication. Bell Syst Tech J. 1948;27(3):379–423.

    Article  MathSciNet  Google Scholar 

  42. Zhou R, Cai R, Tong G. Applications of entropy in finance: a review. Entropy. 2013;15(11):4909–31.

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The authors like to thank the Editor-in-Chief, an associate editor, and anonymous referee for careful reading and useful comments, which have led this improved version. One of the authors, Kousik Maiti, thanks the financial support provided by the MHRD, Government of India. Suchandan Kayal gratefully acknowledges the partial financial support for this research work under a Grant MTR/2018/000350, SERB, India.

Author information

Authors and Affiliations

  1. Department of Mathematics, National Institute of Technology Rourkela, Rourkela, 769008, India

    Kousik Maiti & Suchandan Kayal

  2. Department of Mathematics and Statistics, Indian Institute of Technology Kanpur, Kanpur, 208016, India

    Debasis Kundu

Authors
  1. Kousik Maiti
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Suchandan Kayal
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Debasis Kundu
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Suchandan Kayal.

Ethics declarations

Conflict of interest

We do not have any conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Maiti, K., Kayal, S. & Kundu, D. Statistical Inference on the Shannon and Rényi Entropy Measures of Generalized Exponential Distribution Under the Progressive Censoring. SN COMPUT. SCI. 3, 317 (2022). https://doi.org/10.1007/s42979-022-01200-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42979-022-01200-2

Keywords

Mathematics Subject Classification