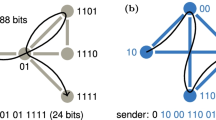
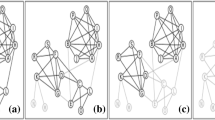
Abstract
We introduce a new class of power centrality measures, which we refer to as Dominance Centrality, for complex networks which may have weighted, directed edges, as well as weights associated with nodes. These measures are similar in spirit to the power-over-powerless class introduced by Bonacich decades ago in the context of eigenvector centrality, but are quite different in their roots and effect. Our Dominance Centrality measure, referred to as DONEX, is derived as a Pareto optimal solution to collective welfare maximisation problem that allocates values to nodes in the network on the basis of expected interaction strengths captured by edge weights between pairs of nodes, where the expectation is taken over the probability of there being an undirected or directed link between them. We show how this formulation yields a new centrality measure which captures the notion of a weighted degree-differential virtual flow along the edges in the network in such a manner that the sum of such flows at each node itself represents the notion of dominance over the neighbourhood. We develop a greedy propagation algorithm called NetProp which allows us to estimate the reach of dominant nodes, and network boundaries where the dominance-derived influence or attention are maximum and minimum. We also demonstrate how DONEX extends to multi-hop neighbourhoods taking account of both local and non-local effects. The new methods are illustrated extensively with synthetic and real networks.


















Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.Availability of data and materials
All data and materials related to the research reported in this work can be made available on request.
Code availability
Software codes related to the research reported in this work can be made available on request.
Notes
Even though the Configuration Model, as explained by Newman in [16], was proposed and examined by many authors in the context of network applications in physics, its variants have found wider utility in the context of community detection problems [60, 61] as a means for defining the notion of modularity [4, 5]. The central premise in the Newman model is that the probability with which a node with degree \(\alpha_{i}\) attaches its edge to another node in a fixed graph with n nodes, is proportional to its own degree, \(\alpha_{i}\), normalised to values < = 1, by dividing by 2 m =|E|, the number of edges in the graph, assuming that the probabilities for the two ends of a single edge are independent of each other. Since the probability that there exists an edge between node i and node j must be symmetric, it must be proportional to the product of their degrees.
This, as is evident, is quite different from deriving directions simply on the basis of degree-differential alone.
Note that the Fiedler vector, obtained from eigenspace of the Laplacian in (16) could also give us a sparse-cut into two clusters of nodes that the connected network could have been split into. But they would have been obtained only on the basis of degree connectivity, and not on the basis of flows which lead to dominance.
References
Katz L. A new status index derived from sociometric analysis. Psychometrika. 1953;18(1):39–43.
Bonacich P. Power and centrality: a family of measures. Am J Sociol. 1987;92(5):1170–82.
Bonacich P. Some unique properties of eigenvector centrality. Soc Netw. 2007;29(4):555–64.
Barabasi A-L. Network Science, http://networksciencebook.com/ July 2016,
Newman MEJ. Networks: an introduction. Oxford: Oxford University Press; 2010.
Page L et al. The PageRank citation ranking: Bringing order to the web, Stanford InfoLab, 1999
Kleinberg JM, et al. The web as a graph: measurements, models, and methods. International Computing and Combinatorics Conference. Springer, Berlin, Heidelberg, 1999.
Xing W, Ghorbani A. Weighted pagerank algorithm. Proceedings. Second Annual Conference on Communication Networks and Services Research, IEEE, 2004.
Langville AN, Meyer CD. Deeper inside pagerank. Internet Math. 2004;1(3):335–80.
Grassi R, Stefani S, Torriero A. Some new results on the eigenvector centrality. Math Sociol. 2007;31(3):237–48.
Benzi M, Estrada E, Klymko C. Ranking hubs and authorities using matrix functions. Linear Algebra Appl. 2013;438(5):2447–74.
Benzi M, Klymko C. A matrix analysis of different centrality measures arXiv preprint arXiv:1312.6722, 2014.
DiStefano JJ, Stubberud AR, Williams IJ, Schaum’s outline of feedback and control systems, signal flow graphs chapter, McGraw-Hill, New York, 2014.
Tsugawa S. Empirical analysis of the relation between community structure and cascading retweet diffusion. Proceedings of the International AAAI Conference on Web and Social Media. Vol. 13. 2019.
Subbanarasimha RP, Srinivasa S, Mandyam S. Invisible stories that drive online social cognition. IEEE Transact Comput Soc Syst. 2020. https://doi.org/10.1109/TCSS.2020.3009474.
Newman, Mark EJ. Finding community structure in networks using the eigenvectors of matrices. Phys Rev E 2006;74(3):036104.
Parzy M, Bogucka H. Coopetition methodology for resource sharing in distributed OFDM-based cognitive radio networks. IEEE Trans Commun. 2014;62(5):1518–29. https://doi.org/10.1109/TCOMM.2014.031214.130451.
Abdel-Hadi A, Clancy C. A utility proportional fairness approach for resource allocation in 4G-LTE. 2014 International Conference on Computing, Networking and Communications (ICNC). IEEE, 2014.
Alexandris K, et al. Utility-based resource allocation under multi-connectivity in evolved LTE. 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall). IEEE, 2017.
Pennings JME, Smidts A. The shape of utility functions and organizational behavior.” Manag Sci, 2003;49(9):1251–1263. JSTOR, www.jstor.org/stable/4134038. Accessed 11 Jul 2021.
Mandyam S, Sridhar U. Loan allocation and guarantee structure for group borrower networks in microfinance. Stud Microecon. 2016;4(2):100–14.
Sridhar U, Mandyam S. DON and shapley value for allocation among cooperating agents in a network: conditions for equivalence. Stud Microecon. 2017;5(2):1–19.
Borgatti SP. Centrality and network flow. Soc Netw. 2005;27(1):55–71.
Bonacich P. A behavioral foundation for a structural theory of power in exchange networks. Soc Psychol Q. 1998;61:185–98.
Hubbell CH. An input–output approach to clique identification. Sociometry. 1965;28:377–99.
Taylor M. Influence structures. Sociometry. 1969;32:490–502.
Coleman JS, Katz E, Menzel H. Medical innovation: a diffusion study. Bobbs-Merrill, Indianapolis. 1966
Freeman LC. Centrality in networks: I. Concept Clarifi Soc Netw. 1979;1:215–39.
Freeman LC, Borgatti SP, White DR. Centrality in valued graphs: a measure of betweenness based on network flow. Soc Netw. 1991;13:141–54.
Friedkin NE. Theoretical foundations for centrality measures. Am J Sociol. 1991;96:1478–504.
Bonacich P, Lloyd P. Eigenvector-like measures of centrality for asymmetric relations. Soc Netw. 2001;23(3):191–201.
Ghosh R, Lerman K. Parameterized centrality metric for network analysis. Phys Rev E. 2011;83(6): 066118.
Bothner MS, Smith EB, White HC. A model of robust positions in social structure. Am J Sociol. 2010;116:943–92.
Rhoades SA. The herfindahl-hirschman index. Fed Res Bull. 1993;79:188.
Singh A, Singh RR, Iyengar SRS. Node-weighted centrality: a new way of centrality hybridization. Comput Soc Netw. 2020;7(1):1–33.
Yang Y, Xie G, Xie J. Mining important nodes in directed weighted complex networks. Discrete Dyn Nat Soc. 2017;2017:7.
Qiao T, Shan W, Zhou C. How to identify the most powerful node in complex networks? A novel entropy centrality approach. Entropy. 2017;19(11):614.
Fei L, Zhang Qi, Deng Y. Identifying influential nodes in complex networks based on the inverse-square law. Physica A. 2018;512:1044–59.
Everett MG, Borgatti SP. The centrality of groups and classes. J Math Soc. 1999;23(3):181–201.
Bonacich P. Simultaneous group and individual centralities. Soc Netw. 1991;13:155–68.
Borgatti SP, Everett MG. A graph-theoretic perspective on centrality. Soc Netw. 2006;28(4):466–84.
Gilles RP. The cooperative game theory of networks and hierarchies. Vol. 44. Springer Science & Business Media, 2010.
del Pozo M, et al. Centrality in directed social networks. A game theoretic approach. Soc Netw. 2011;33(3):191–200.
Grofman B, Owen G. A game theoretic approach to measuring degree of centrality in social networks. Soc Netw. 1982;4(3):213–24.
Skibski O, Michalak TP, Rahwan T. Axiomatic characterization of game-theoretic centrality. J Artif Intell Res. 2018;62:33–68.
Michalak TP, et al. Efficient computation of the Shapley value for game-theoretic network centrality. J Artif Intell Res. 2013;46:607–50.
Khmelnitskaya OS, Talman D. The shapley value for directed graph games. Oper Res Lett. 2016;44:143–7.
Myerson R. Graphs and cooperation in games. Math Oper Res. 1977;2(3):225–9.
Gomez D, et al. Centrality and power in social networks: a game theoretic approach. Math Soc Sci. 2003;46(1):27–54.
Suri N, Narahari Y. Determining the top-k nodes in social networks using the shapley value. In AAMAS ’08: Proceedings of the 7th International Joint Conference on Autonomous Agents and Multi-Agent Systems, pp. 1509–1512 2008.
Michalak T, Aadithya K, Szczepanski P, Ravindran B, Jennings N. Efficient computation of the shapley value for game-theoretic network centrality. J Artif Intell Res. 2013;46:607–50.
Kempe, Kleinberg JM, Tardos E. Maximizing the spread of influence through a social network. In KDD, pp 137:146, 2003.
Li CT, Lin SD, Shan MK. Influence propagation and maximization for heterogeneous social networks. In: Proceedings of the 21st International Conference on World Wide Web; 2012 Apr 16–20; Lyon, France; p. 559–60. 2012.
Zhou C, Zhang P, Zang W, Guo L. On the upper bounds of spread for greedy algorithms in social network influence maximization. IEEE Trans Knowl Data Eng. 2015;27(10):2770–83.
Kreps DM, Microeconomic Foundations I. Choice and competitive markets. Princeton: Princeton University Press; 2013.
Newman MEJ, Strogatz SH, Watts DJ. Random graphs with arbitrary degree distributions and their applications. Phys Rev E. 2001;64: 026118.
Chung F, Lu L. Connected components in random graphs with given degree sequences. Ann Comb. 2002;6:125–45.
Luczak T. Sparse random graphs with a given degree sequence. In: Frieze AM, Luczak T, editors. Proceedings of the symposium on random graphs, Pozna´n 1989. New York: John Wiley; 1992. p. 165–82.
Molloy M, Reed B. A critical point for random graphs with a given degree sequence. Random Struct Algorithms. 1995;6:161–79.
Leicht EA, Newman MEJ. Community structure in directed networks. Phys Rev Lett. 2008;100(11):118703.
Blondel VD, Guillaume J-L, Lambiotte R, Lefebvre E, Fast unfolding of communities in large networks. J Stat Mech 2008(10),P10008(12pp) doi:https://doi.org/10.1088/1742-5468/2008/10/P10008. http://arxiv.org/abs/0803.0476.
Newman MEJ, Girvan M. Finding and evaluating community structure in networks. Phys Rev E. 2004;69: 026113.
Newman MEJ. The structure and function of complex networks. SIAM Rev. 2003;45(2):167–256.
Newman MEJ. Scientific collaboration networks. II. Shortest paths, weighted networks, and centrality. Phys Rev E. 2001;64:016132.
Zachary WW. An information flow model for conflict and fission in small groups. J Anthropol Res. 1977;33(4):452–73.
Mcauley J, Leskovec J. Discovering social circles in ego networks. ACM Transact Knowl Discov Data. 2014;8(1):1–28.
Wang J, Hou X, Li K, Ding Y. A novel weight neighborhood centrality algorithm for identifying influential spreaders in complex networks. Phys A. 2017;S0378–4371(17):30121–8.
Zejun S, Bin W, Jinfang S, Yixiang H, Yihan W, Junming S. Identifying influential nodes in complex networks based on weighted formal concept analysis. IEEE Access 2017;5:3777–3789
Newman MEJ. Analysis of weighted networks. Phys Rev E. 2004;389:2134–42.
Barrat A, Barthélemy M, Pastor-Satorras R, Vespignani A. The architecture of complex weighted networks. Proc Natl Acad Sci USA. 2004;101(11):3747–52.
Li M, Fan Y, Chen J, Gao L, Di Z, Jinshan Wu. Weighted networks of scientific communication: the measurement and topological role of weight. Physica A. 2005;350(2–4):643–65615.
Hougaard JH, Allocation in networks, MIT Press, 2018
Borch K. Economic equilibrium under uncertainty. Int Econ Rev 1968;9(3):339–347
Karlan D, et al. Trust and social collateral. Q J Econ. 2009;124(3):1307–61.
Mobius M, Quoc-Anh D, Rosenblat TS. Social capital in social networks. Retrieved March 3 (2004):2009.
Michalak TP, et al. A new approach to measure social capital using game-theoretic techniques. ACM SIGecom Exchanges. 2015;14(1):95–100.
Jackson MO. Social and economic networks. NJ: Princeton University Press; 2008.
Sridhar Mandyam K, Kumar Dasgupta A, Sridhar U, Dasgupta P, Chakrabarti A. Network approaches in anomaly detection for disease conditions. Biomed Signal Process Control. 2021;68:102659. https://doi.org/10.1016/j.bspc.2021.102659.
Negre CFA, et al. Eigenvector centrality for characterization of protein allosteric pathways. Proc Natl Acad Sci. 2018;115(52):E12201–8.
Agryzkov T, et al. A centrality measure for urban networks based on the eigenvector centrality concept. Environ Plann B. 2019;46(4):668–89.
Rossi RA, Ahmed NK. The network data repository with interactive graph analytics and visualization. Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence. http://networkrepository.com. Accessed 3 Jan 2021.
Acknowledgements
The authors thank anonymous reviewers for comments and suggestions to improve the quality of this paper. The first author thanks Prof Srinath Srinivasa, and research students Raksha RP and Jayati Deshmukh of the Web Science Lab, IIIT, Bangalore for helping to explore many applications of the central ideas of dominance centrality set out in this work, including early versions of DON and DONEX measures. Thanks are also due to Prof Anjan Dasgupta, Department of Biochemistry, Calcutta University, for many illuminating discussions and close collaboration in the development of time-series analysis applications of the basic dominance metrics described here.
Funding
This work has the support of Ecometrix Research.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
There are no conflicts or competing interests in the publication of this research.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Mandyam Kannappan, S., Sridhar, U. A Flow-Based Node Dominance Centrality Measure for Complex Networks. SN COMPUT. SCI. 3, 379 (2022). https://doi.org/10.1007/s42979-022-01270-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42979-022-01270-2