Skip to main content

Advertisement

Springer Nature Link
Log in

Application of Gradient Boosting in Evaluating Surgical Ablation for Atrial Fibrillation

  • Original Research
  • Published:
SN Computer Science Aims and scope Submit manuscript

Abstract

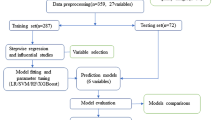
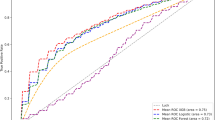
Atrial fibrillation (AF) represents a condition of irregularities of heartbeats. Timely diagnosis and treatment of AF are crucial to avoid serious consequences such as stroke, heart failure and death. AF is detected from patient’s rhythm data as a binary longitudinal sequence. In this article, we introduce an approach for analyzing the binary longitudinal sequence of AF. Our approach is based on gradient boosting, a machine learning approach. We use multivariate tree as a base learner to model complex relationships between multiple covariates and response. In order to model covariate-time interactions, we use B-spline. Application of our approach to a randomized trial data provides the importance of surgical ablation in the treatment of AF among patients with persistent or long-standing persistent AF. Comparison of prediction performance of our approach with other methods using randomized trial data and simulated data shows that our approach has a better prediction performance. Variable selection using variable importance has identified duration of AF as an important covariate that has strong interaction with post-surgery time. This helps to identify patients’ variability and groups of patients who derived the most benefits from the treatment. Our method can be implemented using the R package boostmtree.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Go AS, Hylek EM, Phillips KA, et al. Prevalence of diagnosed atrial fibrillation in adults: national implications for rhythm management and stroke prevention: the AnTicoagulation and Risk Factors in Atrial Fibrillation (ATRIA) Study. J Am Med Assoc. 2001;185(18):2370–5.

    Article  Google Scholar 

  2. Gillinov A, Argenziano M, Blackstone E, Iribarne A, DeRose JJ, et al. Designing comparative effectiveness trials of surgical ablation for atrial fibrillation: experience of the Cardiothoracic Surgical Trials Network. J Thorac Cardiovasc Surg. 2011;142(2):257–64.

    Article  Google Scholar 

  3. Liang KY, Zeger SL. Longitudinal data analysis using generalized linear models. Biometrika. 1986;73:13–22.

    Article  MathSciNet  MATH  Google Scholar 

  4. McCulloch CE, Searle SR. Generalized linear and mixed models. New York: Wiley; 2001.

    MATH  Google Scholar 

  5. Giltinan D, Davidian M. Nonlinear models for repeated measurement data. London: Chapman & Hall; 1995.

    Google Scholar 

  6. Ganesan R, Dhanavanthan P, Kiruthika C, Kumarasamy P, Balasubramanyam D. Comparative study of linear mixed-effects and artificial neural network models for longitudinal unbalanced growth data of Madras Red sheep. Vet World. 2014;7(2):52–8.

    Article  Google Scholar 

  7. Mandel F, Ghosh RP, Barnett I. Neural networks for clustered and longitudinal data using mixed effects models. Biometrics. 2021. https://doi.org/10.1111/biom.13615.

    Article  Google Scholar 

  8. Wood SN. Low rank scale invariant tensor product smooths for generalized additive mixed models. Biometrics. 2006;62(4):1025–36.

    Article  MathSciNet  MATH  Google Scholar 

  9. Pande A, Li L, Rajeswaran J, Ehrlinger J, Kogalur UB, Blackstone EH, Ishwaran H. Boosted multivariate trees for longitudinal data. Mach Learn. 2017;106(2):277–305.

    Article  MathSciNet  MATH  Google Scholar 

  10. Pande A, Ishwaran H, Blackstone E. Boosting for multivariate longitudinal responses. SN Comput Sci. 2022;3:186. https://doi.org/10.1007/s42979-022-01072-6.

    Article  Google Scholar 

  11. Tutz G, Reithinger F. A boosting approach to flexible semi parametric mixed models. Stat Med. 2007;26(14):2872–900.

    Article  MathSciNet  Google Scholar 

  12. Yue M, Li J, Cheng M-Y. Two-step sparse boosting for high dimensional longitudinal data with varying coefficients. Comput Stat Data Anal. 2019;131:222–34.

    Article  MathSciNet  MATH  Google Scholar 

  13. Tutz G, Groll A. Generalized linear mixed models based on boosting. In: Statistical modeling and regression structure. Heidelberg: Physica-Verlag; 2010. p. 197–215.

    Chapter  Google Scholar 

  14. Groll A, Tutz G. Regularization for generalized additive mixed models by likelihood-based boosting. Methods Inf Med. 2012;51(2):168.

    Article  Google Scholar 

  15. Hothorn T, Buhlmann P, Kneib T, Schmid M, Hofner B. Model-based boosting 2.0. J Mach Learn Res. 2010;11:2109–13.

    MathSciNet  MATH  Google Scholar 

  16. Buhlmann P, Yu B. Boosting with L\(_2\) loss: regression and classification. J Am Stat Assoc. 2003;98(462):324–39.

    Article  MATH  Google Scholar 

  17. Friedman JH. Stochastic gradient boosting. Comput Stat Data Anal. 2002;38:367–78.

    Article  MathSciNet  MATH  Google Scholar 

  18. Friedman JH. Greedy function approximation: a gradient boosting machine. Ann Stat. 2001;29:1189–232.

    Article  MathSciNet  MATH  Google Scholar 

  19. De Boor C. A practical guide to splines. Berlin: Springer Verlag; 1978.

    Book  MATH  Google Scholar 

  20. Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and regression trees. Belmont: Wiley; 1984.

    MATH  Google Scholar 

  21. Ishwaran H, Kogalur UB. Random Forests for Survival, Regression and Classification (RF-SRC), 2022. R package version 3.0.2.

  22. Eilers PHC, Marx BD. Flexible smoothing with B-splines and penalties. Stat Sci. 1996;11:89–102.

    Article  MathSciNet  MATH  Google Scholar 

  23. Lu M, Ishwaran H. A prediction-based alternative to P values in regression models. J Thorac Cardiovasc Surg. 2018;155:1130–6.

    Article  Google Scholar 

  24. Gillinov AM, Gelijns AC, Parides MK, DeRose JJ Jr, Moskowitz AJ, et al. Surgical ablation of atrial fibrillation during mitral valve surgery. N Engl J Med. 2015;372(15):1399–408.

    Article  Google Scholar 

  25. Ishwaran H, Pande A, Kogalur U.B. boostmtree: boosted multivariate trees for longitudinal data, 2022. R package version 1.5.1.

  26. Lunn AD, Davies SJ. A note on generating correlated binary variables. Biometrika. 1998;85(2):487–90.

    Article  MathSciNet  MATH  Google Scholar 

  27. Sela RJ, Simonoff JS. RE-EM trees: a data mining approach for longitudinal and clustered data. Mach Learn. 2012;86:169–207.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

This work is supported in part by R01 HL103552 and by a cooperative agreement (U01 HL088942) with the National Heart, Lung, and Blood Institute, including funding by the National Institute of Neurological Disorders and Stroke and the Canadian Institutes of Health Research. Clinicaltrials.gov Identifier: NCT00903370.

Author information

Author notes

  1. Hemant Ishwaran, Eugene Blackstone, Jeevanantham Rajeswaran and Marc Gillinov have contributed equally to this work.

Authors and Affiliations

  1. Heart, Vascular and Thoracic Institute, Cleveland Clinic, 9500 Euclid Avenue, Cleveland, 44016, OH, USA

    Amol Pande, Eugene Blackstone & Marc Gillinov

  2. Division of Biostatistics, University of Miami, 1120 NW 14th St, Miami, 33136, FL, USA

    Hemant Ishwaran

  3. Quantitative Health Sciences, Cleveland Clinic, 9500 Euclid Avenue, Cleveland, 44016, OH, USA

    Eugene Blackstone & Jeevanantham Rajeswaran

Authors
  1. Amol Pande
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Hemant Ishwaran
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Eugene Blackstone
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Jeevanantham Rajeswaran
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Marc Gillinov
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Amol Pande.

Ethics declarations

Conflict of interest

All authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Below is the link to the electronic supplementary material.

Supplementary file1 (PDF 353 KB)

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pande, A., Ishwaran, H., Blackstone, E. et al. Application of Gradient Boosting in Evaluating Surgical Ablation for Atrial Fibrillation. SN COMPUT. SCI. 3, 466 (2022). https://doi.org/10.1007/s42979-022-01350-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42979-022-01350-3

Keywords