Skip to main content
Springer Nature Link
Log in

Sampling and Forecasting Independent Data Via Clustered Bootstrap LSTM Models

  • Original Research
  • Published:
SN Computer Science Aims and scope Submit manuscript

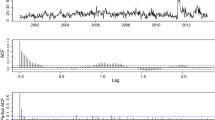
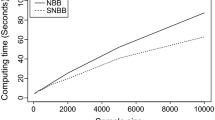
Abstract

In this study we propose a clustered bootstrap sample procedure which adds clustering to the existing bootstrapping techniques currently used in the independent data literature. To assess the improvement of the clustered bootstrap method, we compare it to the existing block bootstrap. We used different data generators to show the improvement introduced by clustering of the blocks and we further validated the practical utility of this method, we apply it to real-world financial data-specifically, the exchange rate between the South African Rand (ZAR) and the US Dollar (USD). The results of this study is measured with the use of the MSE, MAE, MAPE, RMSE and RMSPE. The results from the MSE, MAE and MAPE as well as the DM test all shows that the clustered bootstrap methods shows improvement in forecasting.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Algorithm 1
Algorithm 2
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Availability of Data and Materials

Available on https://www.resbank.co.za/en/home/what-we-do/statistics/key-statistics/selected-historical-rates.

Code Availability

Available on request.

References

  1. Barrow DK, Crone SF. Cross-validation aggregation for combining autoregressive neural network forecasts. Int J Forecast. 2016;32(4):1120–37.

    Article  Google Scholar 

  2. Bashir A, Shehzad MA, Khan A, et al. Use of wavelet and bootstrap methods in streamflow prediction. J Math. 2023;2023.

  3. Beyaztas BH, Firuzan E, Beyaztas U. New block bootstrap methods: sufficient and/or ordered. Commun Stat-Simul Comput. 2017;46(5):3942–51.

    MathSciNet  Google Scholar 

  4. Breiman L. Bagging predictors. Mach Learn. 1996;24(2):123–40.

    Article  Google Scholar 

  5. Bühlmann P, et al. Sieve bootstrap for time series. Bernoulli. 1997;3(2):123–48.

    Article  MathSciNet  Google Scholar 

  6. Carlstein E, et al. The use of subseries values for estimating the variance of a general statistic from a stationary sequence. Ann Stat. 1986;14(3):1171–9.

    Article  MathSciNet  Google Scholar 

  7. Chu H, Bian J, Lang Q, et al. Daily groundwater level prediction and uncertainty using lstm coupled with pmi and bootstrap incorporating teleconnection patterns information. Sustainability. 2022;14(18):11,598.

    Article  Google Scholar 

  8. Dantas TM, Oliveira FLC. Improving time series forecasting: an approach combining bootstrap aggregation, clusters and exponential smoothing. Int J Forecast. 2018;34(4):748–61.

    Article  Google Scholar 

  9. Efron B. Bootstrap methods: another look at the jackknife annals of statistics. 1979;7: 1–26. View Article PubMed/NCBI Google Scholar 24.

  10. Eğrioğlu E, Fildes R. A new bootstrapped hybrid artificial neural network approach for time series forecasting. Comput Econ. 2020;1–29.

  11. Ham YS, Sonu KB, Paek US, et al. Comparison of lstm network, neural network and support vector regression coupled with wavelet decomposition for drought forecasting in the western area of the dprk. Nat Hazards. 2023;116(2):2619–43.

    Google Scholar 

  12. Ivanyuk V. The method of residual-based bootstrap averaging of the forecast ensemble. Financ Innovat. 2023;9(1):1–12.

    Google Scholar 

  13. Kallel R, Cottrell M, Vigneron V. Bootstrap for neural model selection. Neurocomputing. 2002;48(1–4):175–83.

    Article  Google Scholar 

  14. Kourentzes N, Barrow DK, Crone SF. Neural network ensemble operators for time series forecasting. Expert Syst Appl. 2014;41(9):4235–44.

    Article  Google Scholar 

  15. Kuffner T, Lee S, Young G. Block bootstrap optimality and empirical block selection for sample quantiles with dependent data. Biometrika. 2020.

  16. Kumar S, Tiwari MK, Chatterjee C, et al. Reservoir inflow forecasting using ensemble models based on neural networks, wavelet analysis and bootstrap method. Water Resour Manag. 2015;29(13):4863–83.

    Article  Google Scholar 

  17. Kunsch HR. The jackknife and the bootstrap for general stationary observations. Ann Stat. 1989;1217–41.

  18. Lahiri S, Furukawa K, Lee YD. A nonparametric plug-in rule for selecting optimal block lengths for block bootstrap methods. Stat Methodol. 2007;4(3):292–321.

    Article  MathSciNet  Google Scholar 

  19. LePage R, Billard L. Exploring the limits of bootstrap, vol. 270. Amsterdam: Wiley; 1992.

    Google Scholar 

  20. Nordman DJ, Lahiri SN, et al. Convergence rates of empirical block length selectors for block bootstrap. Bernoulli. 2014;20(2):958–78.

    Article  MathSciNet  Google Scholar 

  21. Pan L, Politis DN. Bootstrap prediction intervals for linear, nonlinear and nonparametric autoregressions. J Stat Plan Infer. 2016;177:1–27.

    Article  MathSciNet  Google Scholar 

  22. Politis DN, Romano JP. A circular block-resampling procedure for stationary data. Exploring the limits of bootstrap. 1992;2635270.

  23. Politis DN, Romano JP. The stationary bootstrap. J Am Stat Assoc. 1994;89(428):1303–13.

    Article  MathSciNet  Google Scholar 

  24. Politis DN, White H. Automatic block-length selection for the dependent bootstrap. Economet Rev. 2004;23(1):53–70.

    Article  MathSciNet  Google Scholar 

  25. Ribeiro MHDM, da Silva RG, Moreno SR, et al. Efficient bootstrap stacking ensemble learning model applied to wind power generation forecasting. Int J Electr Power Energy Syst. 2022;136(107):712.

    Google Scholar 

  26. Singh S, Sedory SA. Sufficient bootstrapping. Comput Stat Data Anal. 2011;55(4):1629–37.

    Article  MathSciNet  Google Scholar 

  27. Tiwari MK, Chatterjee C. Development of an accurate and reliable hourly flood forecasting model using wavelet-bootstrap-ann (wbann) hybrid approach. J Hydrol. 2010;394(3–4):458–70.

    Article  Google Scholar 

  28. Tiwari MK, Chatterjee C. Uncertainty assessment and ensemble flood forecasting using bootstrap based artificial neural networks (banns). J Hydrol. 2010;382(1–4):20–33.

    Article  Google Scholar 

  29. Vaish J, Siddiqui KM, Maheshwari Z, et al. Day ahead load forecasting using random forest method with meteorological variables. In: 2023 IEEE Conference on Technologies for Sustainability (SusTech), IEEE, 2023;pp 239–244.

  30. Yolcu U, Egrioglu E, Bas E, et al. Probabilistic forecasting, linearity and nonlinearity hypothesis tests with bootstrapped linear and nonlinear artificial neural network. J Exp Theor Artif Intell. 2021;33(3):383–404.

    Article  Google Scholar 

  31. Zainuddin NH, Lola MS, Djauhari MA, et al. Improvement of time forecasting models using a novel hybridization of bootstrap and double bootstrap artificial neural networks. Appl Soft Comput. 2019;84(105):676.

    Google Scholar 

  32. Zhang J. Developing robust non-linear models through bootstrap aggregated neural networks. Neurocomputing. 1999;25(1–3):93–113.

    Article  Google Scholar 

  33. Zhang W, Quan H, Zhang W, et al. Short-term wind power interval prediction based on gd-lstm and bootstrap techniques. In: 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), IEEE, 2022;pp 2626–2631.

Download references

Funding

Not applicable.

Author information

Authors and Affiliations

  1. Department of Computer Science and Applied Mathematics, University of Witswatersrand, Johannesburg Campus, Johannesburg, 2000, South Africa

    Sihle Kubheka

Authors
  1. Sihle Kubheka
    View author publications

    You can also search for this author inPubMed Google Scholar

Contributions

Not applicable.

Corresponding author

Correspondence to Sihle Kubheka.

Ethics declarations

Conflict of interest

Not applicable.

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kubheka, S. Sampling and Forecasting Independent Data Via Clustered Bootstrap LSTM Models. SN COMPUT. SCI. 5, 171 (2024). https://doi.org/10.1007/s42979-023-02522-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s42979-023-02522-5

Keywords