Skip to main content
Springer Nature Link
Log in

Discrete Stochastic Optimization for Public Health Interventions with Constraints

  • Methodology
  • Published:
Operations Research Forum Aims and scope Submit manuscript

Abstract

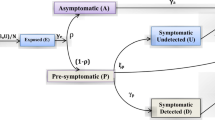
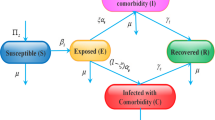
Many public health threats exist, motivating the need to find optimal intervention strategies. Given the stochastic nature of the threats (e.g., the spread of pandemic influenza, the occurrence of drug overdoses, and the prevalence of alcohol-related threats), deterministic optimization approaches may be inappropriate. In this paper, we implement a stochastic optimization method to address aspects of the 2009 H1N1 and the COVID-19 pandemics, with the spread of disease modeled by the open-source Monte Carlo simulations, FluTE, and Covasim, respectively. Without testing every possible option, the objective of the optimization is to determine the best combination of intervention strategies so as to result in minimal economic loss to society. To reach our objective, this application-oriented paper uses the discrete simultaneous perturbation stochastic approximation method (DSPSA), a recursive simulation-based optimization algorithm, to update the input parameters in the disease simulation software so that the output iteratively approaches minimal economic loss. Assuming that the simulation models for the spread of disease (FluTE for H1N1 and Covasim for COVID-19 in our case) are accurate representations for the population being studied, the simulation-based strategy we present provides decision makers a powerful tool to mitigate potential human and economic losses from any epidemic. The basic approach is also applicable in other public health problems, such as opioid abuse and drunk driving.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+
from $39.99 /Month
  • Starting from 10 chapters or articles per month
  • Access and download chapters and articles from more than 300k books and 2,500 journals
  • Cancel anytime
View plans

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Explore related subjects

Discover the latest articles, books and news in related subjects, suggested using machine learning.

Data Availability

The datasets generated during the current study are available from the corresponding author on reasonable request.

Code Availability

Codes are available from the corresponding author on reasonable request.

References

  1. Prosser LA, Lavelle TA, Fiore AE, Bridges CB, Reed C, Jain S, Dunham KM, Meltzer MI (2011) Cost-effectiveness of 2009 pandemic influenza A(H1N1) vaccination in the United States. PloS One 6(7):e22308

    Article  Google Scholar 

  2. Khazeni N, Hutton DW, Garber AM, Hupert N, Owens DK (2009) Effectiveness and cost-effectiveness of vaccination against pandemic influenza (H1N1) 2009. Ann Intern Med 151(12):829–839

    Article  Google Scholar 

  3. Piguillem F, Shi L (2020) Optimal COVID-19 quarantine and testing policies. CEPR Discuss Pap Ser: DP14613

  4. Hoertel N, Blachier M, Blanco C, Olfson M, Massetti M, Limosin F, Leleu H (2020) Facing the COVID-19 epidemic in NYC: a stochastic agent-based model of various intervention strategies. MedRxiv

  5. Charpentier A, Elie R, Laurière M, Tran V (2020) COVID-19 pandemic control: balancing detection policy and lockdown intervention under ICU sustainability. Math Model Nat Phenom 15(57)

  6. Souza PA, Dias CM, Arruda EF (2020) Optimal control model for vaccination against H1N1 flu. Semin Ciênc Exatas Tecnol 41(1):105–114

    Article  Google Scholar 

  7. Hamrock E, Paige K, Parks J, Scheulen J, Levin S (2013) Discrete event simulation for healthcare organizations: a tool for decision making. J Healthc Manag 58(2):110–125

    Google Scholar 

  8. Paleshi A, Bae KH, Evans G, Heragu S (2017) A simulation-based optimization approach for mitigation of pandemic influenza. IISE Trans. Healthc Syst Eng 7(2):107–120

    Article  Google Scholar 

  9. Nelson BL, Swann JL, Goldsman D, Song WT (2001) Simple procedures for selecting the best simulated system when the number of alternatives is large. Oper Res 49:950–963

    Article  Google Scholar 

  10. Chao DL, Halloran ME, Obenchain VJ, Longini IM Jr (2010) FluTE, a publicly available stochastic influenza epidemic simulation model. PLoS Comput Biol 6(1):e1000656

    Article  Google Scholar 

  11. Kerr C, Stuart R, Mistry D, Abeysuriya R, Hart G, Rosenfeld K, Selvaraj P, Nunez RC, Hagedorn B, George L, Izzo A, Palmer A, Delport D, Bennette C, Wagner B, Chang S, Cohen J, Panovska-Griffiths J, Jastrzebski M, Oron A, Wenger E, Famulare M, Klein DJ (2021) Covasim: an agent-based model of COVID-19 dynamics and interventions. PLoS Comput Biol 17(7):e1009149

    Article  Google Scholar 

  12. Wang Q, Spall JC (2014) Discrete simultaneous perturbation stochastic approximation for resource allocation in public health. Am Control Conf 2014:3639–3644

    Google Scholar 

  13. Bureau of Labor Statistics (2021) Consumer price index - all urban consumers, 2000–2020. United States Department of Labor. http://data.bls.gov. Accessed 21 Jan 2021

  14. Wang Q (2013) Optimization with discrete simultaneous perturbation stochastic approximation using noisy loss function measurements. Dissertation, Johns Hopkins University

  15. Wang Q, Spall JC (2011) Discrete simultaneous perturbation stochastic approximation on loss function with noisy measurements. Proc 2011 Am Control Conf: 4520–4525

  16. U.S. Census Bureau (2001) Census 2000 Summary File 1. United States Department of Commerce. https://www.census.gov/data/datasets/2000/dec/summary-file-1.html. Accessed 9 July 2019

  17. U.S. Census Bureau (2011) Census 2010 Summary File 1. United States Department of Commerce. https://www.census.gov/data/datasets/2010/dec/summary-file-1.html. Accessed 9 July 2019

  18. Chao DL, Matrajt L, Basta NE, Sugimoto JD, Dean B, Bagwell DA, Oiulfstad B, Halloran ME, Longini IM Jr (2011) Planning for the control of pandemic influenza A (H1N1) in Los Angeles County and the United States. Am J Epidemiol 173(10):1121–1130

    Article  Google Scholar 

  19. Halder N, Kelso JK, Milne GJ (2011) Cost-effective strategies for mitigating a future influenza pandemic with H1N1 2009 characteristics. PloS One 6(7):e22087

    Article  Google Scholar 

  20. Araz OM, Damien P, Paltiel DA, Burke S, Van De Geijn B, Galvani A, Meyers LA (2012) Simulating school closure policies for cost effective pandemic decision making. BMC Public Health 12(1):449–460

    Article  Google Scholar 

  21. Molinari NA, Ortega-Sanchez IR, Messonnier ML, Thompson WW, Wortley PM, Weintraub E, Bridges CB (2007) The annual impact of seasonal influenza in the US: measuring disease burden and costs. Vaccine 25(27):5086–5096

    Article  Google Scholar 

  22. Spall JC (2003) Introduction to stochastic search and optimization: estimation, simulation, and control. Wiley-Interscience

    Book  Google Scholar 

  23. Basta NE, Chao DL, Halloran ME, Matrajt L, Longini IM Jr (2009) Strategies for pandemic and seasonal influenza vaccination of schoolchildren in the United States. Am J Epidemiol 170(6):679–686

    Article  Google Scholar 

  24. Matsuoka T, Sato T, Akita T, Yanagida J, Ohge H, Kuwabara M, Tanaka J (2016) High vaccination coverage among children during influenza A(H1N1)pdm09 as a potential factor of herd immunity. Int J Environ Res Public Health 13(10):1017–1034

    Article  Google Scholar 

  25. Pasquini-Descomps H, Brender N, Maradan D (2017) Value for money in H1N1 influenza: a systematic review of the cost-effectiveness of pandemic interventions. Value Health 20(6):819–827

    Article  Google Scholar 

  26. Strong A, Welburn JC (2020) An estimation of the economic costs of social-distancing policies. RAND Corporation: RR-A173-1

  27. Thunstrom L, Newbold S, Finnoff D, Ashworth M, Shogren J (2020) The benefits and costs of using social distancing to flatten the curve for COVID-19. J Benefit-Cost Anal 11(2):179–195

    Article  Google Scholar 

  28. U.S. Census Bureau (2020) Census Bureau QuickFacts. United States Department of Commerce. https://www.census.gov/quickfacts/MD. Accessed 23 June 2020

  29. National Center for Education Statistics (2014) Table 2 number of operating public schools and districts, state enrollment, teacher and pupil/teacher ratio by state: school year 2012–13. United States Department of Education. https://nces.ed.gov/pubs2014/2014098/tables/table_02.asp. Accessed 5 July 2020

  30. U.S. Center for Medicare and Medicaid Services (2021) Medicare Administrative Contractor (MAC) COVID-19 Test Pricing. United States Department of Health and Human Services. https://www.cms.gov/files/document/mac-covid-19-test-pricing.pdf. Accessed 18 June 2021

  31. Watson C, Cicero A, Blumenstock J, Fraser M (2020) A national plan to enable comprehensive COVID-19 case finding and contact tracing in the U.S. Association of State and Territorial Health Officials. https://www.centerforhealthsecurity.org/our-work/pubs_archive/pubs-pdfs/2020/200410-national-plan-to-contact-tracing.pdf. Accessed 17 Mar 2021

  32. Bartsch SM, Ferguson MC, McKinnell JA, O’Shea KJ, Wedlock PT, Siegmund SS, Lee BY (2020) The potential health care costs and resource use associated with COVID-19 in the United States. Health Aff 39(6):927–935

    Article  Google Scholar 

  33. Cohen M, Whittal K, Murray T (2020) COVID-19 cost scenario modeling. Wakely consulting group LLC. https://www.ahip.org/documents/AHIP-COVID-19-Modeling.pdf. Accessed 17 Mar 2021

  34. Eichenbaum MS, Rebelo S, Trabandt M (2021) The macroeconomics of epidemics. Rev Financ Stud 34(11):5149–5187

    Article  Google Scholar 

  35. U.S. Centers for Disease Control and Prevention (2020) Options to reduce quarantine for contacts of persons with SARS-CoV-2. United States Department of Health and Human Services. https://www.cdc.gov/coronavirus/2019-ncov/science/science-briefs/scientific-brief-options-to-reduce-quarantine.html. Accessed 10 Aug 2021

  36. Zhang J, Litvinova M, Liang Y, Wang Y, Wang W, Zhao S, Wu Q, Merler S, Viboud C, Vespignani A, Ajelli M, Yu H (2020) Changes in contact patterns shape the dynamics of the COVID-19 outbreak in China. Science 368(6498):1481–1486

    Article  Google Scholar 

  37. Chen S, Yang J, Yang W, Wang C, Bärnighausen T (2020) COVID-19 control in China during mass population movements at New Year. Lancet 395(10226):764–766

    Article  Google Scholar 

  38. Wang L, Zhu J, Spall JC (2018) Mixed simultaneous perturbation stochastic approximation for gradient-free optimization with noisy measurements. Am Control Conf 2018:3774–3779

    Google Scholar 

Download references

Acknowledgements

We thank Yan Zhou and Mengdan Zhang (the Johns Hopkins University) for all the preliminary work done during the course of this research.

Author information

Authors and Affiliations

  1. Northwestern University, Evanston, USA

    Zewei Li

  2. The Johns Hopkins University Applied Physics Laboratory, Laurel, USA

    James C. Spall

Authors
  1. Zewei Li
    View author publications

    Search author on:PubMed Google Scholar

  2. James C. Spall
    View author publications

    Search author on:PubMed Google Scholar

Contributions

JS encouraged ZL to investigate the application of stochastic optimization in public health and supervised the findings of this work. Both authors were involved in developing the methods and algorithms. ZL performed the numerical simulations and analysis. Both authors discussed the results. ZL wrote the final manuscript under the guidance of JS.

Corresponding author

Correspondence to James C. Spall.

Ethics declarations

Ethics Approval

Not applicable.

Consent to Participate

Not applicable.

Consent for Publication

Not applicable.

Conflict of Interest

The authors declare no competing interests.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

Since all the 20 tracts we picked are located within California State and Los Angeles County, the State FPIS code and county FIPS code are 06 and 037 respectively for all tracts. The tract FIPS codes for the selected 20 tracts are 101110, 101120, 101210, 101220, 101300, 101400, 102101, 102102, 103101, 103102, 103200, 103300, 103400, 104103, 104104, 104105, 104106, 104107, 104201, and 104202.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Z., Spall, J.C. Discrete Stochastic Optimization for Public Health Interventions with Constraints. Oper. Res. Forum 3, 68 (2022). https://doi.org/10.1007/s43069-022-00176-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s43069-022-00176-2

Keywords