Skip to main content
SpringerLink
Log in

Deterministic Sensing Matrices Based on Multidimensional Pseudo-Random Sequences

  • Short Paper
  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

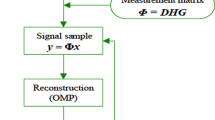
An approach is proposed for producing compressed sensing (CS) matrices via multidimensional pseudo-random sequences. The columns of these matrices are binary Gold code vectors where zeros are replaced by −1. This technique is mainly applied to restore sub-Nyquist-sampled sparse signals, especially image reconstruction using block CS. First, for the specific requirements of message length and compression ratio, a set Λ which includes all preferred pairs of m-sequences is obtained by a searching algorithm. Then a sensing matrix A M×N is produced by using structured hardware circuits. In order to better characterize the correlation between any two columns of A, the average coherence is defined and the restricted isometry property (RIP) condition is described accordingly. This RIP condition has strong adaptability to different sparse signals. The experimental results show that with constant values of N and M, the sparsity bound of A is higher than that of a random matrix. Also, the recovery probability may have a maximum increase of 20 % in a noisy environment.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. A. Amini, F. Marvasti, Deterministic construction of binary, bipolar, and ternary compressed sensing matrices. IEEE Trans. Inf. Theory 57(4), 2360–2370 (2011)

    Article  MathSciNet  Google Scholar 

  2. E.J. Candès, The restricted isometry property and its implications for compressed sensing. C. R. Math. 346(9–10), 589–592 (2008)

    Article  MATH  Google Scholar 

  3. E.J. Candès, T. Tao, Decoding by linear programming. IEEE Trans. Inf. Theory 51(12), 4203–4215 (2005)

    Article  MATH  Google Scholar 

  4. E.J. Candès, M.B. Wakin, An introduction to compressive sampling. IEEE Signal Process. Mag. 25(2), 21–30 (2008)

    Article  Google Scholar 

  5. E.J. Candès, J. Romberg, T. Tao, Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 52(2), 489–509 (2006)

    Article  MATH  Google Scholar 

  6. R. DeVore, Deterministic constructions of compressed sensing matrices. J. Complex. 23(4–6), 918–925 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  7. D.L. Donoho, Compressed sensing. IEEE Trans. Inf. Theory 52(4), 1289–1306 (2006)

    Article  MathSciNet  Google Scholar 

  8. R. Gold, Optimal binary sequences for spread spectrum multiplexing. IEEE Trans. Inf. Theory 13(4), 619–621 (1967)

    Article  MATH  MathSciNet  Google Scholar 

  9. V.D. Goppa, Codes on algebraic curves. Dokl. Akad. Nauk SSSR 259(6), 1289–1290 (1981)

    MathSciNet  Google Scholar 

  10. S.D. Howard, A.R. Calderbank, S.J. Searle, A fast reconstruction algorithm for deterministic compressive sensing using second order Reed–Muller codes, in Proc. IEEE Annual Conf. Inform. Sciences and Systems (CISS), Mar (2008), pp. 11–15

    Google Scholar 

  11. S. Li, F. Gao, G. Ge, S. Zhang, Deterministic construction of compressed sensing matrices via algebraic curves. IEEE Trans. Inf. Theory 58(8), 5035–5041 (2012)

    Article  MathSciNet  Google Scholar 

  12. S. Rao, The theory of cyclic codes and preferred pairs of m-sequences. J. Telem. Track. Command. 11(3), 9–14 (1990)

    Google Scholar 

  13. C.E. Shannon, Communication in the presence of noise. Proc. Inst. Radio Eng. 37(1), 10–21 (1949)

    MathSciNet  Google Scholar 

  14. M. Shen, W. Liu, Image reconstruction technique based on the compressed sensing theory. Electron. Sci. Tech. 24(3), 9–12 (2011)

    Google Scholar 

  15. J.A. Tropp, A.C. Gilbert, Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans. Inf. Theory 53(12), 4655–4666 (2007)

    Article  MathSciNet  Google Scholar 

  16. M.B. Wakin, M.A. Davenport, Analysis of orthogonal matching pursuit using the restricted isometry property. IEEE Trans. Inf. Theory 56(9), 4395–4401 (2010)

    Article  MathSciNet  Google Scholar 

  17. Z. Wan, Algebra and Coding Theory (Higher Education Press, Beijing, 2007)

    Google Scholar 

  18. L.R. Welch, Lower bounds on the maximum cross-correlation of signals. IEEE Trans. Inf. Theory 20(3), 397–399 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  19. N.Y. Yu, Deterministic compressed sensing matrices from additive character sequences (2010). arXiv:1010.0011vl [cs.IT], Sept

  20. N.Y. Yu, Deterministic compressed sensing matrices from multiplicative character sequences, in Proc. IEEE Annual Conf. Inform. Sciences and Systems (CISS), Mar (2011), pp. 1–5

    Google Scholar 

Download references

Acknowledgements

The authors would like to acknowledge funding support from China state 863 Hi-tech programs under No. 2006AA12Z222 and the national Natural Science Foundation of China under No. 2008105GZ30031. The authors are also thankful to the editors and anonymous reviewers for their valuable comments.

Author information

Authors and Affiliations

  1. Department of Geography Science, Nanjing Normal University, Nanjing, 210046, China

    Yan Tang & Guonian Lv

  2. Department of Physics and Technology, Nanjing Normal University, Nanjing, 210046, China

    Kuixi Yin

Authors
  1. Yan Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guonian Lv
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kuixi Yin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yan Tang.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Tang, Y., Lv, G. & Yin, K. Deterministic Sensing Matrices Based on Multidimensional Pseudo-Random Sequences. Circuits Syst Signal Process 33, 1597–1610 (2014). https://doi.org/10.1007/s00034-013-9701-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-013-9701-5

Keywords

Search

Navigation